KMP算法总结 Apare_xzc
KMP算法总结
2020.9.7
KMP算法是什么
- KMP算法是由三位科学共同提出的单模(式串)匹配算法。可以再O(m+n)的时间内完成从文本串text匹配目标串pattern的过程。
- KMP算法的核心是next数组。在匹配的过程中,文本串的指针Pi不回溯,模式串的指针Pj在匹配失败后回溯到next[Pj], 这样就大大减少了匹配的时间。
- 我们先求模式串pattern的next数组,然后通过next数组,去文本串中匹配。
一个例子:
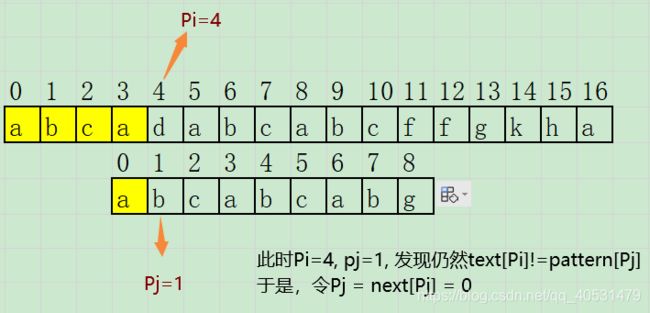
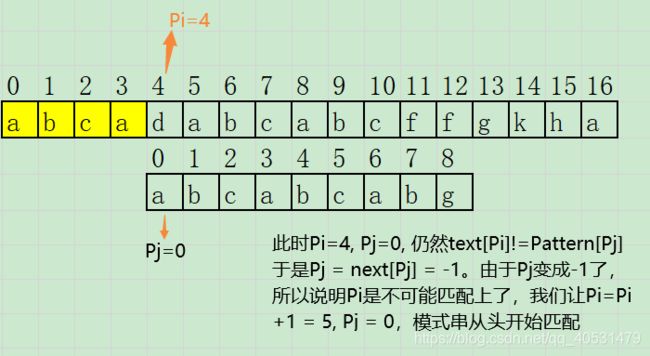
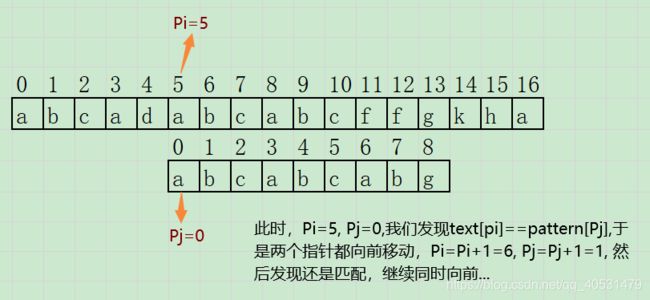
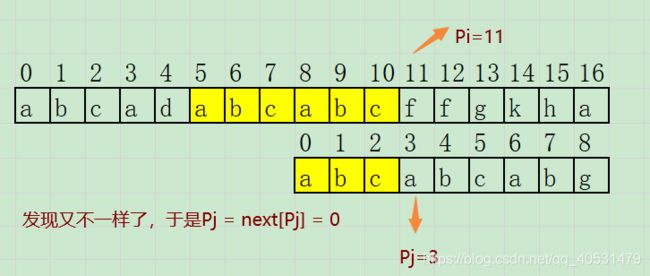
模式串 pattern = abcabcabg,文本串 text = abcadabcabcffgkha
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 字符 | a | b | c | a | b | c | a | b | g | ‘\0’ |
| nextval | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 0 | 0 |
| next | -1 | 0 | 0 | 0 | 1 | 2 | 3 | 4 | 5 | 0 |
其中nextval[x]代表以x结尾的后缀串的末尾和前缀串最大相同的字符数。但是前缀串和后缀串不能相同。所以nextval[0] = 0, 那为什么nextval[7]=5呢?
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | a | b | c | a | b | g | ‘\0’ | |
| a | b | c | a | b | c | a |
我们看到,以s[7]结尾的后缀,和前缀串相同的字符最多有5个,所以nextval[7] = 5
next数组是怎么来的呢?我们观察可以得到:next数组就是nextval数组整体向右移动了一个单元,然后next[0] = -1

后面的过程依次类推。
如果Pj走到了Pattern的末尾,说明匹配成功了。如果Pi走到了末尾,还没匹配成功,那么说明匹配失败。
- next[x]的含义是,模式串在pattern[Pj]这个位置没有匹配成功,那么如果next[Pj]=t,说明
Pattern[0,1,2,3...t-1]和Pattern[Pj-t...Pj-2,Pj-1]这两个子串是相同的,所以Pattern[0,1,2,3...t-1]和text[Pi-t...Pi-2,Pi-1]也是相同的。 - 所以我们可以令
Pj=next[x] = t,直接从Pattern[t]和text[i]开始比较。
所以,我们可以写出KMP匹配的代码了:
int getFirstMathchPos(const string& text,const string& pattern,const vector<int>& next) {
int lent = text.length(), lenp = pattern.length();
int i = 0, j = 0; //初始化指针i,j均为0,从文本串头部和模式串的头部开始匹配
while(i<lent) { //如果文本串指针i到头了,说明匹配完了
if(j==-1||pattern[j]==text[i]) { //如果pattern[j]==text[i],说明相等,一起往前
++i; ++j; //如果j==-1了,就说明i也该++了
if(j==lenp) return i-lenp; //如果j走到了模式串尾,说明匹配到了,我们返回文本串
//最开始匹配到Pattern[0]的位置
}
else j = next[j];
}
return -1; //说明没匹配上,返回-1
}
那么next数组怎么求呢?next数组其实就是在 Pattern串的后缀上,匹配Pattern的前缀,所以写法差不多。
vector<int> getNext(string pattern) {
int lenp = pattern.length();
vector<int> next(lenp+2,0); //这里写lenP+1的话,重复匹配的时候会越界
int i = 0, j = -1;
next[0] = -1;
while(i<=lenp) {
if(j==-1||pattern[i]==pattern[j])
++i, ++j, next[i] = j; //记录next[i]=j
else
j = next[j];
}
return next;
}
KMP的基础应用
- 匹配模式串在文本串第一次出现的位置。代码在上面
- 计算模式串在文本串中出现的次数
- 可以重叠:HihoCoder-1015
int getCountOfMatchMax(const string& text,const string& pattern,const vector<int>& next) {
int lent = text.length(), lenp = pattern.length(), cnt = 0;
int i = 0, j = 0;
while(i<lent) {
if(j==-1||pattern[j]==text[i]) {
++i;++j;
if(j==lenp) ++cnt, j = next[j]; //可以重叠的实现就在这里,请自己体会
}
else
j = next[j];
}
return cnt;
}
- 不可以重叠
int getCountOfMatchMin(const string& text,const string& pattern,const vector<int>& next) {
int lent = text.length(), lenp = pattern.length(), cnt = 0;
int i = 0, j = 0;
while(i<lent) {
if(j==-1||pattern[j]==text[i]) {
++i;++j;
if(j==lenp) ++cnt, j = 0;
}
else
j = next[j];
}
return cnt;
}
int getMaxPalindromePrefixLength(const string& s) { //求最长回文前缀的长度
string text = s;
reverse(text.begin(),text.end());
const string& pattern = s;
vector<int> next = getNext(pattern);
int i = 0, j = 0, len = s.length();
while(i<len) {
if(j==-1||text[i]==pattern[j])
++i, ++j;
else j = next[j];
}
return j;
}
知道了最长回文前缀的长度,就可以在字符串开头添加字符变成最短的回文串了
string Push_front_to_palindrome(const string& s) { //前面加字符变最短回文串
int len = s.length();
if(!len) return s;
string ans;
int Len = getMaxPalindromePrefixLength(s);
for(int i=len-1;i>=Len;--i)
ans += s[i];
ans += s;
return ans;
}
- 计算最长回文后缀串的长度同理:
int getMaxPalindromeSuffixLength(const string& s) { //求最长回文后缀的长度
const string& text = s;
string pattern = s;
reverse(pattern.begin(),pattern.end());
vector<int> next = getNext(pattern);
int i = 0, j = 0, len = text.length();
while(i<len) {
if(j==-1||text[i]==pattern[j])
++i, ++j;
else j = next[j];
}
return j;
}
在字符串尾部追加字符称为回文串:
string Push_back_to_palindrome(const string& s) { //尾部追加字符串变最短回文串
int len = s.length();
if(!len) return s;
string ans = s;
int Len = getMaxPalindromeSuffixLength(s);
for(int i=len-Len-1;i>=0;--i)
ans += s[i];
return ans;
}
- 一个应用,HDU-3336, 求所有前缀串在字符串中匹配的总次数。
思路是利用next数组,对于以每个位置x结尾的字符,只要next[x]>0, 说明就有一个长度为next[x]的前缀与以它为结尾的串匹配。那么,我们可以对每个位置,迭代k=next[k],直到K为0,就停止,计数迭代了多少次。这样会很慢,我们可以记忆化一下,把之前算过的记下来。
int getCountOfAllPrefixMatch(const string& s,const int mod=10007) { //HUD-3366求所有前缀匹配字符串的总次数
vector<int> next = getNext(s);
int len = s.length();
vector<int> sum(len+2,-1); //sum[i]记录长度为i的前缀被匹配的次数
sum[0] = 0;
for(int i=1;i<=len;++i) {
int k = next[i];
int ans = 1;
while(k>0) {
++ans;
k = next[k];
if(sum[k]!=-1) {
ans += sum[k];break;
}
}
sum[i] = ans;
}
int res = 0;
for(int i=1;i<=len;++i)
res = (res+sum[i])%mod;
return res;
}
代码汇总
#include next = KMP::getNext(pattern);
// cout<
// }
// string s;
// while(cin>>s) {
cout<
cout<
// cout<
// }
int T,n;
string s;
cin>>T;
while(T--) {
cin>>n>>s;
cout<<KMP::getCountOfAllPrefixMatch(s)<<"\n";
}
return 0;
}
2020.9.7
16:24