百度飞桨-手把手带你零基础实践深度学习-课程笔记（二）

手写数字识别

数字识别是计算机从纸质文档、照片或其他来源接收、理解并识别可读的数字的能力，目前比较受关注的是手写数字识别。手写数字识别是一个典型的图像分类问题，已经被广泛应用于汇款单号识别、手写邮政编码识别等领域，大大缩短了业务处理时间，提升了工作效率和质量。

在处理如 图所示的手写邮政编码的简单图像分类任务时，可以使用基于MNIST数据集的手写数字识别模型。MNIST是深度学习领域标准、易用的成熟数据集，包含60000条训练样本和10000条测试样本.

• 任务输入：一系列手写数字图片，其中每张图片都是28x28的像素矩阵。
• 任务输出：经过了大小归一化和居中处理，输出对应的0~9的数字标签。

MNIST数据集

手写数字识别的模型是深度学习中相对简单的模型，非常适用初学者。正如学习编程时，我们输入的第一个程序是打印“Hello World！”一样。 在飞桨的入门教程中，我们选取了手写数字识别模型作为启蒙教材，以便更好的帮助读者快速掌握飞桨平台的使用.

大多数示例使用手写数字的MNIST数据集。该数据集包含60,000个用于训练的示例和10,000个用于测试的示例。这些数字已经过尺寸标准化并位于图像中心，图像是固定大小**(28x28像素)**，其值为0到9。为简单起见，每个图像都被平展并转换为784(28 * 28)个特征的一维numpy数组。

构建手写数字识别的神经网络模型

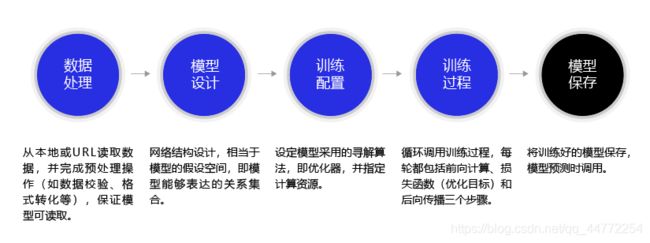
使用飞桨完成手写数字识别模型任务的代码结构如 图所示，与使用飞桨完成房价预测模型任务的流程一致，下面的章节中我们将详细介绍每个步骤的具体实现方法和优化思路

• 飞桨各模型代码结构一致，大大降低了用户的编码难度
  在探讨手写数字识别模型的实现方案之前，我们先看一下部分程序代码。不难发现，与上一章学习的房价预测模型的代码比较，二者是极为相似的
  

• 从代码结构上看，模型均为数据处理、定义网络结构和训练过程三个部分。

• 从代码细节来看，两个模型也很相似。
  这就是使用飞桨框架搭建深度学习模型的优势，只要完成一个模型的案例学习，其它任务即可触类旁通。在工业实践中，程序员用飞桨框架搭建模型，无需每次都另起炉灶，多数情况是先在飞桨模型库中寻找与目标任务类似的模型，再在该模型的基础上修改少量代码即可完成新的任务

• 教程采用"横纵式"教学法，适用于深度学习初学者
  
  这种“横纵式”教学法的设计思路尤其适用于深度学习的初学者，具有如下两点优势：

• 帮助读者轻松掌握深度学习内容：采用这种方式设计教学案例，读者在学习过程中接收到的信息是线性增长的，在难度上不会有阶跃式的提高。

• 模拟真实建模的实战体验：先使用熟悉的模型构建一个可用但不够出色的基础版本（Baseline），再逐渐分析每个建模环节可优化的点，一点点的提升优化效果，让读者获得真实建模的实战体验。

在“横纵式”教学法中，纵向概要介绍模型的基本代码结构和极简实现方案。横向深入探讨构建模型的每个环节中，更优但相对复杂的实现方案。例如在模型设计环节，除了在极简版本使用的单层神经网络（与房价预测模型一样）外，还可以尝试更复杂的网络结构，如多层神经网络、加入非线性的激活函数，甚至专门针对视觉任务优化的卷积神经网络

接下来我们将逐步学习建模的方法。

• 前提条件
  在数据处理前，首先要加载飞桨与手写数字识别模型相关的类库，实现方法如下

import paddle
import paddle.fluid as fluid
from paddle.fluid.dygraph.nn import Linear
import numpy as np
import os
from PIL import Image

数据处理

飞桨提供了多个封装好的数据集API，涵盖计算机视觉、自然语言处理、推荐系统等多个领域，帮助读者快速完成深度学习任务。如在手写数字识别任务中，通过paddle.dataset.mnist可以直接获取处理好的MNIST训练集、测试集，飞桨API支持如下常见的学术数据集：

• mnist
• cifar
• Conll05
• imdb
• imikolov
• movielens
• sentiment
• uci_housing
• wmt14
• wmt16

通过 paddle.dataset.mnist.train() 函数导入训练集，并设置数据读取器，batch_size设置为8，即一个批次有8张图片和8个标签，代码如下所示

# 如果～/.cache/paddle/dataset/mnist/目录下没有MNIST数据，API会自动将MINST数据下载到该文件夹下
# 设置数据读取器，读取MNIST数据训练集
trainset = paddle.dataset.mnist.train()
# 包装数据读取器，每次读取的数据数量设置为batch_size=8
train_reader = paddle.batch(trainset, batch_size=8)

paddle.batch 函数将MNIST数据集拆分成多个批次，通过如下代码读取第一个批次的数据内容，观察打印结果
注：
enumerate方法：用于将一个可遍历的数据对象(如列表、元组或字符串)组合为一个索引序列，同时列出数据和数据下标
语法：

enumerate(sequence, [start=0])

其中，sequence为遍历对象，start为起始位置

举例：

seasons = ['spring', 'summer', 'autumn', 'winter']
for sea_num, season in enumerate(seasons, start = 1):
	print(sea_num, season)
输出：
1 spring
2 summer
3 autumn
4 winter

# 以迭代的形式读取数据
for batch_id, data in enumerate(train_reader()):
    # 获得图像数据，并转为float32类型的数组
    img_data = np.array([x[0] for x in data]).astype('float32')
    # 获得图像标签数据，并转为float32类型的数组
    label_data = np.array([x[1] for x in data]).astype('float32')
    # 打印数据形状
    print("图像数据形状和对应数据为:", img_data.shape, img_data[0])
    print("图像标签形状和对应数据为:", label_data.shape, label_data[0])
    break

print("\n打印第一个batch的第一个图像，对应标签数字为{}".format(label_data[0]))
# 显示第一batch的第一个图像
import matplotlib.pyplot as plt
img = np.array(img_data[0]+1)*127.5 #反归一化
img = np.reshape(img, [28, 28]).astype(np.uint8)

plt.figure("Image") # 图像窗口名称
plt.imshow(img)
plt.axis('on') # 关掉坐标轴为 off
plt.title('image') # 图像题目
plt.show()
输出：
图像数据形状和对应数据为: (8, 784) [-1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -0.9764706  -0.85882354 -0.85882354 -0.85882354
 -0.01176471  0.06666672  0.37254906 -0.79607844  0.30196083  1.
  0.9372549  -0.00392157 -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -0.7647059  -0.7176471  -0.26274508  0.20784318
  0.33333337  0.9843137   0.9843137   0.9843137   0.9843137   0.9843137
  0.7647059   0.34901965  0.9843137   0.8980392   0.5294118  -0.4980392
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -0.6156863
  0.8666667   0.9843137   0.9843137   0.9843137   0.9843137   0.9843137
  0.9843137   0.9843137   0.9843137   0.96862745 -0.27058822 -0.35686272
 -0.35686272 -0.56078434 -0.69411767 -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -0.85882354  0.7176471   0.9843137
  0.9843137   0.9843137   0.9843137   0.9843137   0.5529412   0.427451
  0.9372549   0.8901961  -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -0.372549    0.22352946 -0.1607843   0.9843137
  0.9843137   0.60784316 -0.9137255  -1.         -0.6627451   0.20784318
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -0.8901961  -0.99215686  0.20784318  0.9843137  -0.29411763
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.          0.09019613  0.9843137   0.4901961  -0.9843137  -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -0.9137255
  0.4901961   0.9843137  -0.45098037 -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -0.7254902   0.8901961
  0.7647059   0.254902   -0.15294117 -0.99215686 -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -0.36470586  0.88235295  0.9843137
  0.9843137  -0.06666666 -0.8039216  -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -0.64705884  0.45882356  0.9843137   0.9843137
  0.17647064 -0.7882353  -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -0.8745098  -0.27058822  0.9764706   0.9843137   0.4666667
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.          0.9529412   0.9843137   0.9529412  -0.4980392  -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -0.6392157   0.0196079   0.43529415  0.9843137
  0.9843137   0.62352943 -0.9843137  -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -0.69411767  0.16078436
  0.79607844  0.9843137   0.9843137   0.9843137   0.9607843   0.427451
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -0.8117647  -0.10588235  0.73333335  0.9843137   0.9843137   0.9843137
  0.9843137   0.5764706  -0.38823527 -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -0.81960785 -0.4823529   0.67058825  0.9843137
  0.9843137   0.9843137   0.9843137   0.5529412  -0.36470586 -0.9843137
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -0.85882354  0.3411765
  0.7176471   0.9843137   0.9843137   0.9843137   0.9843137   0.5294118
 -0.372549   -0.92941177 -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -0.5686275   0.34901965  0.77254903  0.9843137   0.9843137   0.9843137
  0.9843137   0.9137255   0.04313731 -0.9137255  -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.          0.06666672  0.9843137
  0.9843137   0.9843137   0.6627451   0.05882359  0.03529418 -0.8745098
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.         -1.         -1.
 -1.         -1.         -1.         -1.        ]
图像标签形状和对应数据为: (8,) 5.0

打印第一个batch的第一个图像，对应标签数字为5.0

图像以数组的形式存储，每个数字代表相应位置像素的灰度值（归一化处理后）；如果我们想打印图片观察，需要进行反归一化处理

从打印结果看，从数据加载器train_reader()中读取一次数据，可以得到形状为（8, 784）的图像数据和形状为（8,）的标签数据。其中，形状中的数字8与设置的batch_size大小对应，784为MINIST数据集中每个图像的像素大小(28*28)

此外，从打印的图像数据来看，图像数据的范围是[-1, 1]，表明这是已经完成图像归一化后的图像数据，并且空白背景部分的值是-1。将图像数据反归一化，并使用matplotlib工具包将其显示出来，如图所示。可以看到图片显示的数字是5，和对应标签数字一致

说明：
飞桨将维度是28x28的手写数字图像转成向量形式存储，因此使用飞桨数据加载器读取到的手写数字图像是长度为784（28x28）的向量

飞桨API的使用方法

熟练掌握飞桨API的使用方法，是使用飞桨完成各类深度学习任务的基础，也是开发者必须掌握的技能，下面介绍飞桨API获取方式和使用方法

1.飞桨API文档获取方式

登录“飞桨官网->文档->API Reference”，获取飞桨API文档

2.通过搜索和分类浏览两种方式查阅API文档

• 如果用户知道需要查阅的API名称，可通过页面右上角的搜索框，快速获取API。
• 如果想全面了解飞桨API文档内容，也可以在API Reference首页，单击 “API功能分类”，通过概念分类获取不同职能的API
  
  在API功能分类的页面，读者可以根据神经网络建模的逻辑概念来浏览相应部分的API，如优化器、网络层、评价指标、模型保存和加载等

3.API文档使用方法

飞桨每个API的文档结构一致，包含接口形式、功能说明和计算公式、参数和返回值、代码示例四个部分。 以abs函数为例，API文档结构如 图所示。通过飞桨API文档，读者不仅可以详细查看函数功能，还可以通过可运行的代码示例来实践API的使用

模型设计

在房价预测深度学习任务中，我们使用了单层且线性变换的模型，取得了理想的预测效果。在手写数字识别任务中，我们依然使用这个模型预测输入的图形数字值。其中，模型的输入为784维（2828）数据，输出为1维数据，如图所示

输入像素的位置排布信息对理解图像内容非常重要（如将原始尺寸为2828图像的像素按照7112的尺寸排布，那么其中的数字将不可识别），因此网络的输入设计为2828的尺寸，而不是1*784，以便于模型能够正确处理像素之间的空间信息。

事实上，采用只有一层的简单网络（对输入求加权和）时并没有处理位置关系信息，因此可以猜测出此模型的预测效果有限。在后续优化环节中，介绍的卷积神经网络则更好的考虑了这种位置关系信息，模型的预测效果也会显著提升。

下面以类的方式组建手写数字识别的网络，实现方法如下所示

# 定义mnist数据识别网络结构，同房价预测网络
class MNIST(fluid.dygraph.Layer):
    def __init__(self):
        super(MNIST, self).__init__()
        
        # 定义一层全连接层，输出维度是1，激活函数为None，即不使用激活函数
        self.fc = Linear(input_dim=784, output_dim=1, act=None)
        
    # 定义网络结构的前向计算过程
    def forward(self, inputs):
        outputs = self.fc(inputs)
        return outputs

训练配置

训练配置需要先生成模型实例（设为“训练”状态），再设置优化算法和学习率（使用随机梯度下降SGD，学习率设置为0.001），实现方法如下所示

# 定义飞桨动态图工作环境
with fluid.dygraph.guard():
    # 声明网络结构
    model = MNIST()
    # 启动训练模式
    model.train()
    # 定义数据读取函数，数据读取batch_size设置为16
    train_loader = paddle.batch(paddle.dataset.mnist.train(), batch_size=16)
    # 定义优化器，使用随机梯度下降SGD优化器，学习率设置为0.001
    optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001, parameter_list=model.parameters())

训练过程

训练过程采用二层循环嵌套方式，训练完成后需要保存模型参数，以便后续使用。

• 内层循环：负责整个数据集的一次遍历，遍历数据集采用分批次（batch）方式。
• 外层循环：定义遍历数据集的次数，本次训练中外层循环10次，通过参数EPOCH_NUM设置。

# 通过with语句创建一个dygraph运行的context
# 动态图下的一些操作需要在guard下进行
with fluid.dygraph.guard():
    model = MNIST()
    model.train()
    train_loader = paddle.batch(paddle.dataset.mnist.train(), batch_size=16)
    optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.001, parameter_list=model.parameters())
    EPOCH_NUM = 10
    for epoch_id in range(EPOCH_NUM):
        for batch_id, data in enumerate(train_loader()):
            #准备数据，格式需要转换成符合框架要求
            image_data = np.array([x[0] for x in data]).astype('float32')
            label_data = np.array([x[1] for x in data]).astype('float32').reshape(-1, 1)
            # 将数据转为飞桨动态图格式
            image = fluid.dygraph.to_variable(image_data)
            label = fluid.dygraph.to_variable(label_data)
            
            #前向计算的过程
            predict = model(image)
            
            #计算损失，取一个批次样本损失的平均值
            loss = fluid.layers.square_error_cost(predict, label)
            avg_loss = fluid.layers.mean(loss)
            
            #每训练了1000批次的数据，打印下当前Loss的情况
            if batch_id !=0 and batch_id  % 1000 == 0:
                print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy()))
            
            #后向传播，更新参数的过程
            avg_loss.backward()
            optimizer.minimize(avg_loss)
            model.clear_gradients()

    # 保存模型
    fluid.save_dygraph(model.state_dict(), 'mnist')

通过观察上述代码可以发现，手写数字识别的代码与房价预测任务几乎一致，如果不是下述读取数据的两行代码有所差异，往往会误认为这是房价预测的模型

#准备数据，格式需要转换成符合框架要求
   image_data = np.array([x[0] for x in data]).astype('float32')
   label_data = np.array([x[1] for x in data]).astype('float32').reshape(-1, 1)

另外，从训练过程中Loss发生的变化可以发现，虽然Loss整体上在降低，但到训练的最后一轮，Loss值依然较高。可以猜测手写数字识别完全复用房价预测的代码，训练效果并不好。接下来我们通过模型测试，获取模型训练的真实效果

模型测试

模型测试的主要目的是验证训练好的模型是否能正确识别出数字，包括如下四步：

• 声明实例
• 加载模型：加载训练过程中保存的模型参数。
• 灌入数据：将测试样本传入模型，模型的状态设置为校验状态（eval），显式告诉框架我们接下来只会使用前向计算的流程，不会计算梯度和梯度反向传播。
• 获取预测结果，取整后作为预测标签输出。
  在模型测试之前，需要先从（预先保存）’./example_0.jpg’文件中读取样例图片，并进行归一化处理。

# 导入图像读取第三方库
import matplotlib.image as mpimg
import matplotlib.pyplot as plt
import cv2
import numpy as np
# 读取图像
img1 = cv2.imread('./example_0.png')
example = mpimg.imread('./example_0.png')
# 显示图像
plt.imshow(example)
plt.show()
im = Image.open('./example_0.png').convert('L')
print(np.array(im).shape)
im = im.resize((28, 28), Image.ANTIALIAS)
plt.imshow(im)
plt.show()
print(np.array(im).shape)
输出：

(252, 255)

(28, 28)

# 读取一张本地的样例图片，转变成模型输入的格式
def load_image(img_path):
    # 从img_path中读取图像，并转为灰度图
    im = Image.open(img_path).convert('L')
    print(np.array(im))
    im = im.resize((28, 28), Image.ANTIALIAS)
    im = np.array(im).reshape(1, -1).astype(np.float32)
    # 图像归一化，保持和数据集的数据范围一致
    im = 1 - im / 127.5
    return im

# 定义预测过程
with fluid.dygraph.guard():
    model = MNIST()
    params_file_path = 'mnist'
    img_path = './work/example_0.png'
# 加载模型参数
    model_dict, _ = fluid.load_dygraph("mnist")
    model.load_dict(model_dict)
# 灌入数据
    model.eval()
    tensor_img = load_image(img_path)
    result = model(fluid.dygraph.to_variable(tensor_img))
#  预测输出取整，即为预测的数字，打印结果
    print("本次预测的数字是", result.numpy().astype('int32'))
输出：
[[255 255 255 ... 255 255 255]
 [255 255 255 ... 255 255 255]
 [255 255 255 ... 255 255 255]
 ...
 [255 255 255 ... 255 255 255]
 [255 255 255 ... 255 255 255]
 [255 255 255 ... 255 255 255]]
本次预测的数字是 [[4]]

从打印结果来看，模型预测出的数字是与实际输出的图片的数字不一致。这里只是验证了一个样本的情况，如果我们尝试更多的样本，可发现许多数字图片识别结果是错误的。因此完全复用房价预测的实验并不适用于手写数字识别任务！

接下来我们会对手写数字识别实验模型进行逐一改进，直到获得令人满意的结果。