Scala实现神经网络 ANN , 偏函数式风格

为了加深理解,用Scala实现全链接的二分类神经网络, 风格偏函数式, 没有使用循环, 不使用var变量, 需要使用Breeze线性代数库.

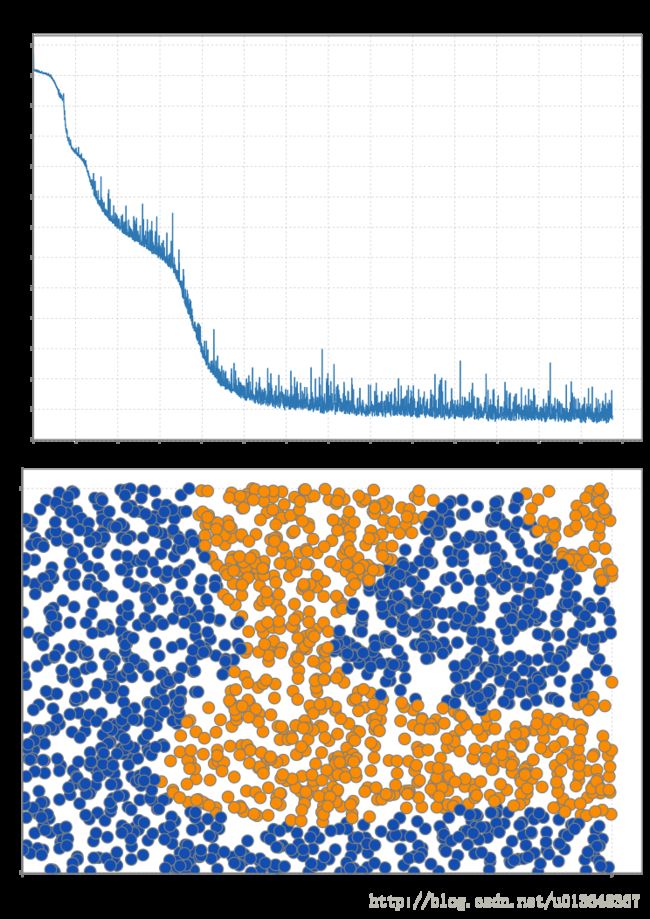
用Python制造了一组相对难分的训练数据并写入文件,如图.

代码如下
先导入一些库

package ann
import java.io.File 
import breeze.linalg.{*, max, min, sum, DenseMatrix => BDM, DenseVector => BDV} //那个*号居然是广播运算用的
import breeze.linalg.InjectNumericOps
import breeze.{numerics => BN} // 导入函数库 
import breeze.plot._ //作图库
import scala.annotation.tailrec
import scala.math
import scala.util.Random

定义网络, 神经网络的本质就是一个函数, 给个输入,有个输出

//封装一下网络参数, 主要是权重,偏置和激活函数
case class LayerPara(weight:BDM[Double] , bias:BDV[Double],activationFunc: ActivationFunc)

trait Layer{
  def apply(input:BDM[Double] ):BDM[Double]
  //定一个类似List的操作,表示网络链接
  def <=:(nextLayerPara:LayerPara):HLayer = HLayer(nextLayerPara,this) //这是个具体方法, 会被直接装配到子类里面
}
//输入层只有一个, 弄个单例
object Input extends Layer{
  def apply(input:BDM[Double] ):BDM[Double]  = input
}
//隐层, 
case class HLayer( layerPara:LayerPara,next:Layer ) extends Layer{
  val w:BDM[Double] = layerPara.weight
  val b:BDV[Double] = layerPara.bias
  def apply(input: BDM[Double]  ):BDM[Double] = {
    val net = next(input) * w
    layerPara.activationFunc( net(*,::)+b )
  }
}

定义激活函数

trait ActivationFunc{
  def apply(x: BDM[Double]  ): BDM[Double]
  def derivative(x:BDM[Double]  ): BDM[Double]
}

object ActivationFunc {
  object sigmoid extends ActivationFunc {
    @inline
    def apply(x: BDM[Double]  ): BDM[Double]  = 1.0 /:/ (1.0 +:+ BN.exp(-x))
    def derivative(x: BDM[Double]  ): BDM[Double]   = sigmoid(x) *:* (1.0 -:- sigmoid(x)) //把导数也定义了
  }

  object relu extends ActivationFunc{
    @inline
    def apply(x: BDM[Double]):BDM[Double] = x.map(v=>if(v>0.0) v else 0.0)
    def derivative(x: BDM[Double]): BDM[Double] = x.map(v=> if (v>0.0) 1.0 else 0.0)
  }
}

读文件

  def fileLoader(file: String): (BDM[Double] , BDM[Double] ) = {
    val dataRaw = breeze.linalg.csvread(new File(file))
    val dataMat = dataRaw(::, 0 to -2) //取到倒数第二列
    val labels = dataRaw(::,-1) //取最后一列
    (dataMat, labels.toDenseMatrix.t)
  }

更新网络, 输入一批数据, 更新产生一个新的网络,而不是修改原处

  def update(batch:BDM[Double],net:HLayer, error:BDM[Double],learnRate:Double):HLayer={
    val size = batch.rows.toDouble
    val nextOut = net.next(batch) //下一层的输出
    val errorTerm = net.layerPara.activationFunc.derivative({val netValue = nextOut * net.w; netValue(*,::) + net.b}) *:* error //计算误差项
    val del_w = ( nextOut.t * errorTerm ) *:* learnRate /:/ size //w的改变量
    val del_b =  sum(errorTerm(::,*)).t  *:* learnRate /:/ size //b的改变量
    net.next match {
      case Input => HLayer(LayerPara(net.w -:- del_w ,net.b -:- del_b, net.layerPara.activationFunc),Input)
      case nextLayer:HLayer => HLayer(LayerPara(net.w -:- del_w ,net.b -:- del_b, net.layerPara.activationFunc),
                                      update(batch,nextLayer, errorTerm * net.w.t, learnRate )) //递归地将误差传下去
    }
  }

用尾递归代替循环进行训练

  @tailrec
  def train(trainData:BDM[Double],labels:BDM[Double],dataLength:Int,
            net:HLayer,
            learnRate:Double,
            batchSize:Int,
            maxIter:Int, ii:Int=0,
            trainErrorLog:Array[Double]= new Array[Double](0)): (HLayer,Array[Double]) ={

    val batchStart = Random.nextInt(dataLength - batchSize)
    val slice = batchStart until (batchStart+batchSize)
    val batch = dataMat(slice,::)
    val netUpdated = update(batch,net, net(batch) -:- labels(slice,::),learnRate)

    val newLog = {
      if (ii % 20 == 0) {
        val trainError = 0.5 * sum( BN.pow(netUpdated(trainData) -:- labels,2) )
        println("训练误差:" + trainError)
        trainErrorLog :+ trainError
      }
      else {
        trainErrorLog
      }
    }

    if (ii>=maxIter) (netUpdated, trainErrorLog)
    else train(trainData,labels,dataLength,netUpdated,learnRate,batchSize,maxIter,ii+1,newLog)
  }

主程序, 需要把上面的函数定义加入进来的

object ANN extends App{
  import ActivationFunc.{sigmoid, relu}
  val (dataMat, label) = fileLoader("./ANNTestData.csv")
  //初始化各层参数
  val l1=LayerPara(BDM.zeros[Double](2,10).map(_+Random.nextGaussian()/math.sqrt(10)),BDV.zeros(10),relu)
  val l2=LayerPara(BDM.zeros[Double](10,8).map(_+Random.nextGaussian()/math.sqrt(8)),BDV.zeros(8),sigmoid)
  val l3=LayerPara(BDM.zeros[Double](8,6).map(_+Random.nextGaussian()/math.sqrt(6)),BDV.zeros(6),relu)
  val l4=LayerPara(BDM.zeros[Double](6,1).map(_+Random.nextGaussian()/math.sqrt(1)),BDV.zeros(1),sigmoid)

  val initNet = l4<=:l3<=:l2<=:l1<=:Input // 串接网络
  //训练 , 传入数据, 标签, 数据大小, 初始网络, 学习率0.28, 大小为50的批次, 训练55000步.
  val (trainedNet, errorLog) = train(dataMat,label,dataMat.rows,initNet,0.28,50,55000)

//下面是作图的
//作出误差
  val f = Figure()
  f.width = 600
  f.height = 800
  val sub = f.subplot(2,1,0)
  val ranges =BDV.range(0,errorLog.length).map(_.toDouble)
  sub += plot(ranges,BDV(errorLog))

//作出分类结果
  val sub2 = f.subplot(2,1,1)
  val x = dataMat(::,0)
  val y = dataMat(::,1)
  val newLabels = trainedNet(dataMat)
  val colorPalette = GradientPaintScale(0.0, 1.0, PaintScale.Rainbow)
  sub2 += scatter(x,y,_ =>0.02, i=> if (newLabels(i,0)<0.5) colorPalette(0.86) else colorPalette(0.26))
  f.saveas("ann.pdf")

结果如图

结果表明神经网络作出了基本正确的分类