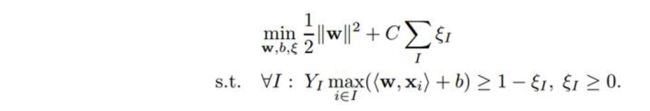CV理论基础（四）：未有深度学习之前——人脸检测、行人检测
计算机视觉理论基础（四）
- 人脸检测
- Haar-like特征
- Haar级联分类器
- 弱分类器和强分类器
- 行人检测
- HOG 方向梯度直方图
- SVM
- Multiple-instance SVM
- Latent SVM
- Deformable Part Model
- 模型组成
- 响应函数
- 检测流程
- 相关资料
检测 ≠ \neq =识别
人脸检测
Haar-like特征+级联分类器
Haar-like特征
特征模板有白色和黑色两种矩形，定义模板的特征值为白色矩形内的像素和减去黑色矩形内的像素和
-
用处：表示人脸的某些特征
具体见CV理论基础（三）：基于关键点的特征描述子sift、surf、orb等；LBP、Gabor -
Haar-like特征数量选择
模板15种、位置、缩放相互组合
Haar级联分类器
利用Adaboost。级联分类器是将多个强分类器连接在一起进行操作，每一个强调分类器由若干个弱分类器加权组成。
强分类器拼接成级联分类器如图所示：
作为负例去除的一定不是人脸
弱分类器拼接成强分类器如图所示：
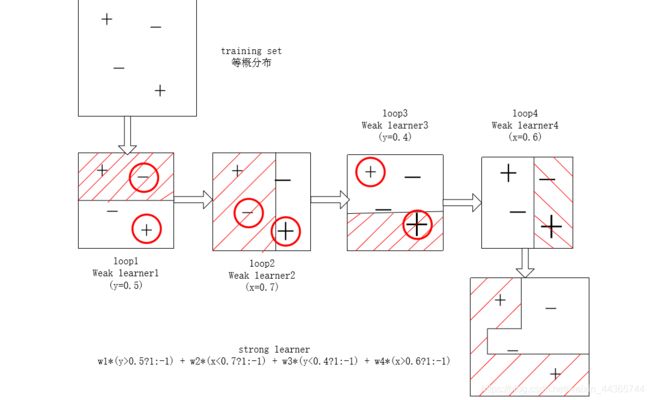
弱分类器和强分类器
弱分类器：选取特征，以稍低于50%的错误率区分人脸或非人脸图像。训练弱分类器是在当前权重分布情况下，确定f的最优阈值，使弱分类器对所有训练样本的分类误差最低。
强分类器：将每轮得到的最佳弱分类器按照一定方法Boosting，构造强分类器。强分类器对负样本更敏感
行人检测
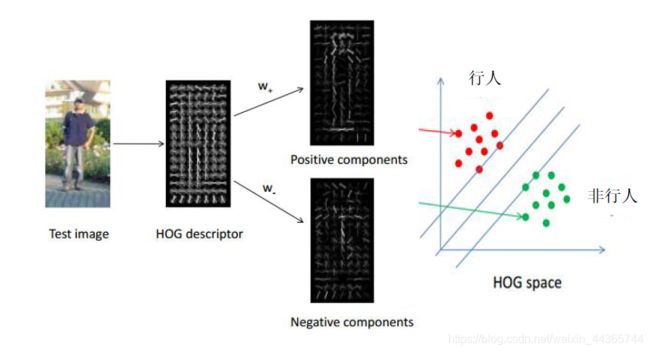
HOG+SVM
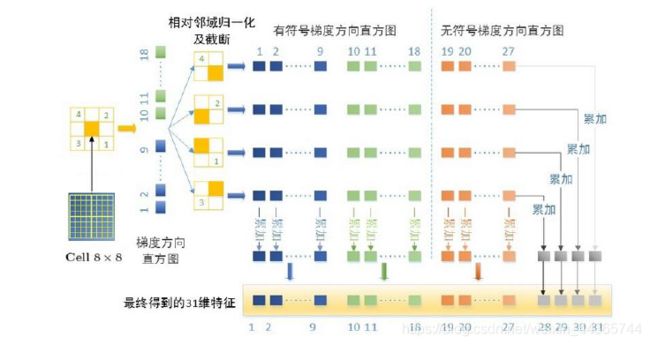
HOG 方向梯度直方图
梯度是一个矢量。 ∇ f ( x , y ) = [ G x G y ] T = [ ∂ f ∂ x ∂ f ∂ y T ] \nabla f(x,y)=[G_xG_y]^T=[\frac {\partial f }{\partial x}\frac {\partial f }{\partial y}^T ] ∇f(x,y)=[GxGy]T=[∂x∂f∂y∂fT]。其中， G x G_x Gx是沿x方向上的梯度， G y G_y Gy是沿y方向上的梯度，梯度的幅值，绝对值大小，方向角表示如下：
∇ f ( x , y ) = { m a g ( ∇ f ( x , y ) ) = G x 2 + G y 2 1 2 ϕ ( x , y ) = a r c t a n ( G y G x ) \nabla f(x,y)= \begin{cases} mag(\nabla f(x,y))={{G_x}^2+{G_y}^2}^{\frac{1}{2}} \\ \phi (x,y)=arctan(\frac{G_y}{G_x})\end{cases} ∇f(x,y)={mag(∇f(x,y))=Gx2+Gy221ϕ(x,y)=arctan(GxGy)
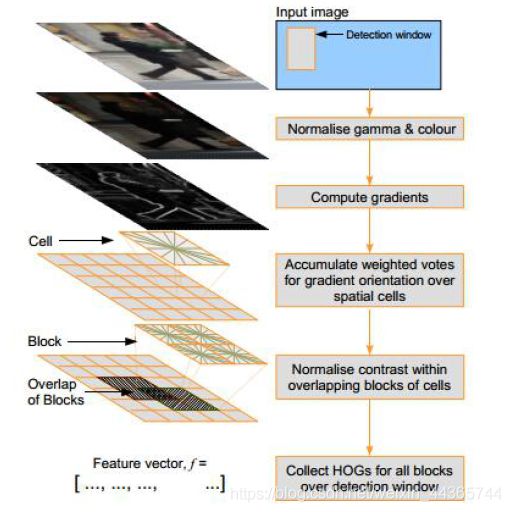
步骤如下：
（1） 将整个图像进行Gamma空间、颜色归一化
（2）图像梯度计算
分别计算水平、垂直梯度的幅值和方向
注意：彩色图，选取梯度幅值最大的通道
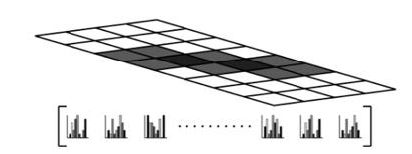
（3）Block拆分
定义两种数据结构的单位：Cell、Block，避免明暗光照的影响
一个Block包含 2 × 2 2 \times 2 2×2个Cell，每个Cell是 8 × 8 8 \times 8 8×8个pixel
一幅图 16 × 16 16 \times 16 16×16个Block，步长是8，50%重合
（4）构建方向的直方图
-
计算Cell的梯度方向直方图：
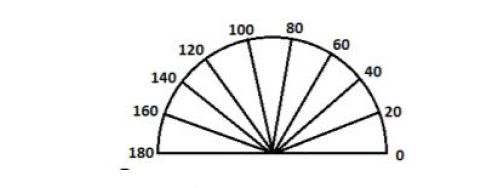
使用位置高斯加权，进行平滑。将0-180度分为9个bin，相邻bin使用线性插值，如85，与80距离5，离100距离15， 1 4 \frac{1}{4} 41归到80， 3 4 \frac{3}{4} 43归到100。归属于哪里，积累相应的梯度幅值。
三线性插值，x方向，y方向，bin分配 -
串接所有Block直方图
例如 64 × 128 64 \times 128 64×128图片，形成 7 × 15 = 105 7 \times 15 =105 7×15=105个Block，共有 105 × ( 2 × 2 ) × 9 = 3780 105 \times (2 \times 2) \times 9=3780 105×(2×2)×9=3780维
（5）将细胞单元组合成更大的空间，对比度归一化
梯度幅值绝对值大小容易受前景背景对比度和局部光照影响，所以需要对局部细胞单元进行对比度归一化处理，L2范式或L1范式。
经过此步骤HOG描述符变成由各区间所有细胞单元的直方图成分所组成的一个向量，区间相互重叠，每一个细胞单元的输出都多次作用于最终的描述器。
（6）收集HOG特征
SVM
基本模型：线性可分情况下，将正类和反类训练样本使用超平面完全正确分开，间隔最小。
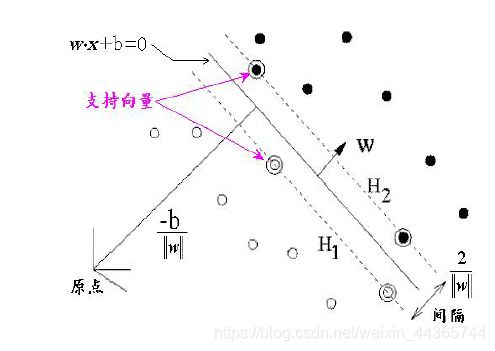
模型允许错分样本，引入松弛变量，不但要使两类样本之间的间隔尽量大，同时还要使错分的样本的松弛变量之和尽可能小，
存在线性不可分数据时，通过非线性映射f（x）把数据由低维空间向高维空间映射，在高维空间为低维数据构造线性可分离超平面。该分离超平面对应原特征空间一个分割超曲面。
Multiple-instance SVM
思想：将标准SVM的最大化样本间距扩展为最大化样本集间距。具体来说是选取正样本集中最像正样本的样本用作训练。
目标：保证正样本中有正，负样本不能为正。
Latent SVM
实际上和MI-SVM相同，区别在于扩展了Latent变量。
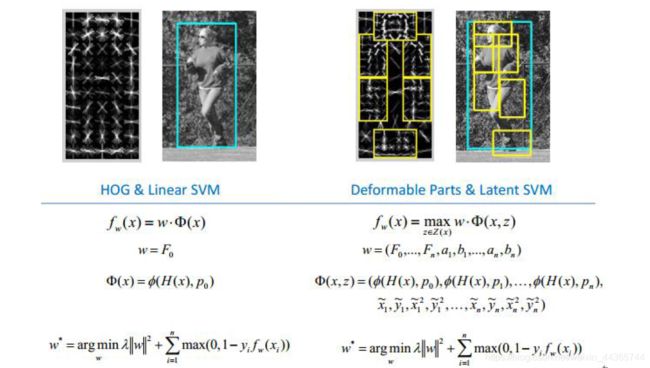
Deformable Part Model
可变形的组件模型是一种基于组件的检测算法，经典算法。
模型组成
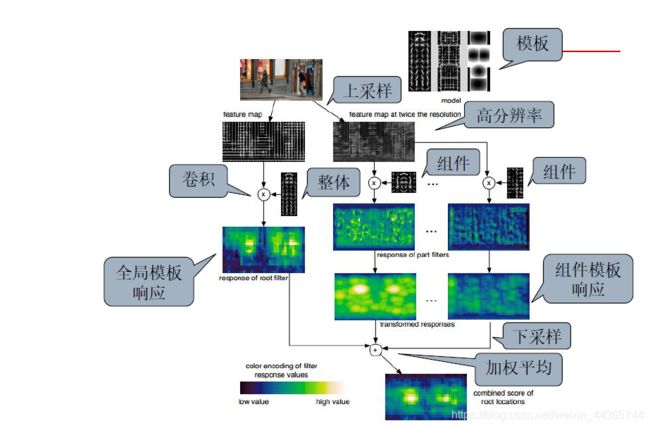
模型包含一个 8 ∗ 8 8*8 8∗8分辨率的根滤波器（Root filter）——看整体形状响应,如左图所示
和一个 4 ∗ 4 4*4 4∗4分辨率的组件滤波器（Part filter）——上采样高斯得到高分辨率，如中图所示
响应函数
s c o r e ( x 0 , y 0 , l 0 ) = R 0 ， l 0 ( x 0 , y 0 ) + ∑ i = 1 n D i , l 0 − λ ( 2 ( x 0 , y 0 ) + v i ) + b score(x_0,y_0,l_0)=R_{0，l_0}(x_0,y_0)+\sum_{i=1}^n D_{i,l_0-\lambda}(2(x_0,y_0)+v_i)+b score(x0,y0,l0)=R0，l0(x0,y0)+i=1∑nDi,l0−λ(2(x0,y0)+vi)+b
x 0 , y 0 , l 0 x_0,y_0,l_0 x0,y0,l0分别是锚点的横坐标，纵坐标，尺度
R 0 ， l 0 ( x 0 , y 0 ) R_{0，l_0}(x_0,y_0) R0，l0(x0,y0)是根模型的响应分数
D i , l 0 − λ ( 2 ( x 0 , y 0 ) + v i ) D_{i,l_0-\lambda}(2(x_0,y_0)+v_i) Di,l0−λ(2(x0,y0)+vi)是部件模型的响应分数
b b b是不同模型组件之间的偏移系数，加上这个偏移量使其与跟模型进行对齐
2 ( x 0 , y 0 ) 2(x_0,y_0) 2(x0,y0)表示组件模型的像素为原始的2倍
检测流程
（1）将输入图像，提取DPM特征图，进行高斯金字塔上采样，提取其DPM特征图
（2）将原始图像DPM特征图和训练好Root filter做卷积操作，从而得到Root filter的响应图
（3）2倍图像的DPM特征图，和训练好的Part filter做卷积操作，从而得到Part filter的响应图
（4）对精细高斯金字塔的下采样操作，Root filter的响应图和Part filter的响应图具有相同的分辨率
（5）进行加权平均，得到最终的响应图。亮度越大表示响应值越大。
相关资料
DPM
在Python中使用HOG-Linear SVM进行人体检测