【解题报告】Codeforces Round #409 (rated, Div. 2, based on VK Cup 2017 Round 2)
题目链接
A. Vicious Keyboard(Codeforces 801A)
思路
本题的入手点在于,由于最多只能修改一个字符,所以可以枚举被修改的字符。
枚举被修改的字符,然后统计 VK 出现的次数,更新答案。注意还可以不是用修改的机会
代码
#include B. Valued Keys(Codeforces 801B)
思路
本题的入手点在于寻找最特殊的构造方式。
设输入的字符串为 x 和 z 。我们要寻找满足 f(x,y)=z 的 y 。若 z 中某位置出现比 x 中对应位置字典序大的字符,那么就无解。否则一定有解,并且我们可以贪心地令 y=z 来构造 y 。
代码
#include C. Voltage Keepsake(Codeforces 801C)
思路
本题的入手点是,寻找最值比较麻烦,但判定值是否满足条件比较容易。于是可以利用二分查找来解决问题。
首先先判断什么时候有无穷解。显然,当充电的速度大于设备的耗电速度之和的时候可以用无限地使用设备。
在剩下的有解的情况中,寻找最值是比较麻烦了,但判定某个解 t 是否满足条件还是比较容易的。假设 ok(t) 判定表示所有设备坚持使用t单位的时间是否有问题的函数,我们现在要完成这个函数的编写。显然我们可以计算出在 t 时间内所有设备的总用电量和 t 时间内设备能够充上的总电量,比较它们的大小就能完成 ok(t) 的功能了。
利用这个函数进行二分查找,不断地通过判断答案区间中点的解是否满足条件来缩小答案区间,知道最后得到问题的解。
代码
#include D. Volatile Kite(Codeforces 801D)
思路
本题的入手点是,所有点的可移动距离为 d ,那么所有点的移动范围为一个圆,于是可以将问题转化为静态的几何问题。
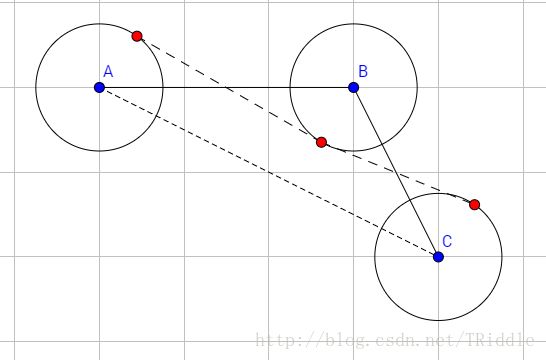
所有点可以移动到某个圆的边界和圆内的所有点所在的位置,那么请看下图:
(图片来源(http://codeforces.com/blog/entry/51598))
我们现在来探究多边形不凹的条件。对于任意三个点 A,B,C ,以它们为圆心 d 为半径分别画三个圆。点 A,B,C 最远可分别移动到圆 A,B,C 上。图中的红点就是它们移动后的点。可以直观地看出,圆 B 上的红点必须离线段 AC 足够远,若圆 B 上的红点靠近到圆 AC 上的红点之间的虚线以内,那么最后生成的多边形就可能是凹的。那么,只要点 B 到直线 AC 的距离大于或等于 2d 就能保证最后生成的多变形不凹了。
因为对于任意三个点都是如此,所以只要求出任意三点 A,B,C 之间 B 到线段 AC 的最小值 Min ,令 d=Min2 就可以得到答案 d 。现在问题转化成求任意三点 A,B,C 的 B 到线段 AC 的最小值 Min 。
枚举三个点肯定是会超时的,所以必须另辟蹊径。我们注意到,最后的答案一定在 A,B,C 三个点相邻的情况下求出的点到线段距离之中(这些一定是最短的)。于是我们按照顺时针顺序(或逆时针顺序)枚举点 A ,计算点到直线距离的同时更新答案即可。
代码
#include