交通流量预测-混合注意力时空图卷积-ASTGCN
Attention Based Spatial-Temporal Graph Convolutional Networks for Traffic Flow Forecasting
- 论文简介
- 论文背景
- 摘要
- 相关研究
- 论文所做的工作
- 符号定义和问题定义
- ASTGCN实现
- 时空注意力
- 时空图卷积
- 空间维卷积
- 时间维卷积
- 多组件融合
- 实验
- 总结与展望
- 思考
论文简介
发表时间:2019 AAAI
发表单位:北京交通大学
论文链接:https://aaai.org/ojs/index.php/AAAI/article/download/3881/3759
PPT链接:https://github.com/Davidham3/ASTGCN/blob/master/ASTGCN_ppt.pdf
论文背景
交通预测是智能交通系统的关键一环。特别是对于高速公路的车流量预测来说,由于高速公路车流大,车速快,一旦发生拥堵则会严重影响交通容量。因此如果能够提前预测流量高峰,疏散交通,就能够避免拥堵的产生,因此这个问题是有意义的。
高速公路车流预测是一个典型的时空数据预测问题,本文主要围绕此问题开展了研究。选取的数据集是PeMS,来自于加州的公路记录仪。
摘要
交通流量预测是交通领域研究人员和实践者面临的一个关键问题。然而,由于交通流通常表现出高非线性和复杂的模式,这是一个非常具有挑战性的问题。现有的交通流量预测方法大多缺乏对交通数据时空动态相关性建模的能力,无法得到满意的预测结果。本文提出了一种基于注意力的时空图卷积网络(ASTGCN)模型来解决交通流预测问题。ASTGCN主要由三个独立的组件组成,分别对交通流的三个时间特性进行建模。当前依赖、日周期依赖和周周期依赖。更具体地说,每个组件包含两个主要部分:1)时空注意机制,有效地捕捉交通数据的动态时空相关性;2)时空卷积,同时使用图形卷积来捕捉空间模式,使用常用标准卷积来描述时间特征。这三个分量的输出被加权融合以产生最终的预测结果。来自PeMS的实验数据表明,提出的ASTGCN模型优于当前的最优模型。
相关研究
| 模型分类 | 具体算法 | 缺点 |
|---|---|---|
| 传统时间序列分析 | HA,ARIMA | 难以处理不稳定、非线性数据 |
| 传统机器学习 | SVM | 虽然能够处理复杂数据,但是(1)难以同步考虑高维交通数据的时空相关性(2)依赖于特征工程,需要较多专家经验 |
| 传统深度学习 | CNN,LSTM | 虽然可以提取时空特征,但是只能处理结构化的2D或者3D等规则数据 |
| 基于图的深度学习 | GCN,Chebynet,GGCN | 没有同时考虑动态时空相关性 |
作者觉得他们都不行,因此作者提出将注意机制和时空数据的特点结合起来。
论文所做的工作
- 开发了一个时空注意机制来学习交通数据的动态时空关联。具体地说,空间注意被用于模型之间的复杂的空间相关性的不同位置。时间关注应用于捕获不同时间之间的动态时间相关性。
- 为建立交通数据的时空相关性模型,设计了一种新的时空卷积模型。它包括从原始的基于图的交通网络结构中获取空间特征的图形卷积和描述邻近时间片依赖关系的时间维度卷积
- 在现实世界的高速公路交通数据集上进行了大量的实验,取得了最佳效果
符号定义和问题定义
本文将交通网络定义为一个无向图G=(V,E,A)V是节点集合,共有N个。E是边集,A是邻接矩阵(N*N)。每个节点的特征向量为F,有三个属性,流量flow,车速speed,占用occupy如b图所示。

符号定义:

问题定义:
| 变量 | 含义 |
|---|---|
| (输出)Y= ( y 1 , y 2 , . . . , y N ) T ∈ R N × T p (y^1,y^2,...,y^N)^T ∈ R^{N×T_p} (y1,y2,...,yN)T∈RN×Tp | 交通网络上的所有节点在接下来的 τ p \tau_p τp个时间片的流量值, |
| y i y^i yi= ( y τ + 1 i , y τ + 2 i , . . , y τ + T p i ) (y^i_{\tau+1},y^i_{\tau+2},..,y^i_{\tau+T_p}) (yτ+1i,yτ+2i,..,yτ+Tpi) | 表示节点i从 τ + 1 \tau+1 τ+1到 τ + T p \tau+T^p τ+Tp时刻的流量值。 |
X,包含交通网络上的所有节点过去T个时间片的测量数据,需要预测的未来交通流量序列为Y = ( y 1 , y 2 , . . . , y N ) T ∈ R N × T p (y^1,y^2,...,y^N)T ∈ R^{N×T^p} (y1,y2,...,yN)T∈RN×Tp,其含义是整个交通网络上的所有节点在接下来的 T p T_p Tp个时间片的流量值, y i = ( y τ + 1 i , y τ + 2 i , . . , y τ + T p i ) y^i=(y^i_{\tau+1},y^i_{\tau+2},..,y^i_{\tau+T_p}) yi=(yτ+1i,yτ+2i,..,yτ+Tpi) 表示节点i从 τ + 1 \tau+1 τ+1到 τ + T p \tau+T^p τ+Tp时刻的流量值。
ASTGCN实现
框架主要包含3个部分,分别提取邻近、日、周依赖特征。recent部分包含邻近的T个时段,daily-period 部分包含前一天或多天与预测时段相同的多个时间序列,weekly-period部分前一周或多周与预测时段相同的多个时间序列。该三部分具有相同的网络结构,每部分由多个时空块和一个全连接层组成。在每个时空块中都有时空注意力模块和时空卷积模块。为了优化训练效率,文章采用了残差连接。最后,利用一个参数矩阵对三个分量加权合并,得到最终预测结果。下面对时空注意力模块和时空卷积模块进行详细介绍。
假设采样频率为q次/天。假设当前时间为t0,预测窗口大小为Tp。如图4所示,我们在时间轴上截取长度为Th、Td和Tw的三个时间序列片段,分别作为相邻、日周期和周周期分量的输入,其中Th、Td和Tw都是Tp的整数倍:

时空注意力
数据在时间和空间上都是有着较强的关联度。
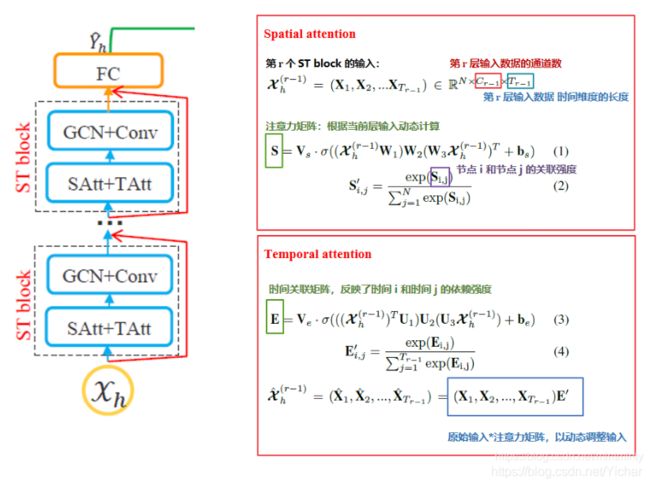
对于空间注意力: V s , b s ∈ R N ∗ N , W 1 ∈ R T r − 1 , W 2 ∈ R C r − 1 × T r − 1 , W 3 ∈ R C r − 1 V_s,b_s \in R^{N*N},W_1 \in R^{T_r-1},W_2 \in R^{C_{r-1} \times T_r-1},W_3 \in R^{C_r-1} Vs,bs∈RN∗N,W1∈RTr−1,W2∈RCr−1×Tr−1,W3∈RCr−1 都是可学习参数。应用图卷积时,将会用邻接矩阵A和 S ’ ∈ R N ∗ N S^’ \in R^{N*N} S’∈RN∗N一起动态调整权值生成节点的注意力系数。
同理时间注意力也是如此,不同的是这里直接把原始输入 χ 和 E ’ \chi和E^’ χ和E’
相乘作为新的输入 χ ^ h ( r − 1 ) \hat{\chi}{_h}^{(r-1)} χ^h(r−1)。
时空图卷积

经过注意力层的处理之后,那些对来说更有价值的数据被相对提取了出来,将新的数据输入到时空卷积模块,同样也分为时间和空间2个部分:
空间维卷积
采用的是谱域方法,也就是基于图拉普拉斯矩阵 L = I N − D ( − 1 / 2 ) A D ( − 1 / 2 ) ∈ R ( N × N ) L=I_N-D^{(-1/2)}AD^{(-1/2})\in R^{(N\times N)} L=IN−D(−1/2)AD(−1/2)∈R(N×N)进行特征分解而进行的图卷积方法,具体的卷积公式如下:

⨀ \bigodot ⨀表示哈达玛乘积: c i j = a i j ∗ b i j c_{ij}=a_{ij}*b_{ij} cij=aij∗bij
*G 表示某种图卷积操作,此处选用的是cheby-conv.
g θ g_\theta gθ表示可学习参数
时间维卷积

*表示标准卷积,此处应该是1D-conv,将样本时间点的前后数据也一起融合了一下,得到了整个模块的最终输出.
多组件融合

这个公式是不言自喻的,其实可以理解成三个周期数据的注意力模型.
实验
总结与展望
这篇论文,从多个时间周期上(相邻,天,周)设计了一个多路网络结构,每个分支上由多个ST BLOCK组成,而ST BLOCK=(Satt+Tatt)+(GCN+conv):先用注意力机制提取更有效的时间和空间特征,再输入给卷积层,卷积层中,用图卷积提取空间特征,用标准卷积提取时间特征,最后将注意力层和卷积层堆叠,完成ST BLOCK的构建.在PeMSD4和PeMSD8中取得了最佳效果.
作者说还可以加入天气和社会事件等特征来丰富结果.理论上特征越多越好做.但是数据集我们去哪里搞呢?
思考
PeMSD4和PeMSD8都是比较小的数据集(几百个节点),本文的方法能否在更大更复杂的数据集上也取得最好的效果呢?

