动态规划 蓝桥杯模拟赛 摆动序列 带你手撕动态规划
这个题网上有很多动态规划的解法,可能是我太菜的原因,不讲得很详细我是不会懂的,于是我自己重新梳理了一遍。尽量能让所有人都能知道该怎么用动态规划去解决这个问题。本文有点长,主要记录了分析的整个过程,图文并茂,相信像我这样的小白也能搞懂动态规划。体验一把手撕动态规划的感觉。
文章目录
- 题目
- 思考
-
-
- 动态规划=动态递推
-
- 思考
-
-
- 动态规划的例题
- 编程解决
-
- 代码一(未优化)
-
- 思考
-
-
- 代码
- 代码二(优化)
-
- 思考
- 代码
- 注意点
- 总结
-
- 什么是动态规划呢?
-
-
- 结束语
题目
问题描述
如果一个序列的奇数项都比前一项大,偶数项都比前一项小,则称为一个摆动序列。即 a[2i]
小明想知道,长度为 m,每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
输入格式
输入一行包含两个整数 m,n。
输出格式
输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
样例输入
3 4
样例输出
14
样例说明
以下是符合要求的摆动序列:
2 1 2
2 1 3
2 1 4
3 1 2
3 1 3
3 1 4
3 2 3
3 2 4
4 1 2
4 1 3
4 1 4
4 2 3
4 2 4
4 3 4
评测用例规模与约定
对于 20% 的评测用例,1 <= n, m <= 5;
对于 50% 的评测用例,1 <= n, m <= 10;
对于 80% 的评测用例,1 <= n, m <= 100;
对于所有评测用例,1 <= n, m <= 1000。
思考
这个题目要求的是摆动序列的数目。那什么是摆动序列呢? 要保证任意的奇数项 > 前一个偶数项,任意偶数项 < 前一个奇数项。需要注意的是单独的一项也是一个合法的摆动序列。比如当m=1,n=2的时候,合法的摆动序列为1和2。如下图所示:
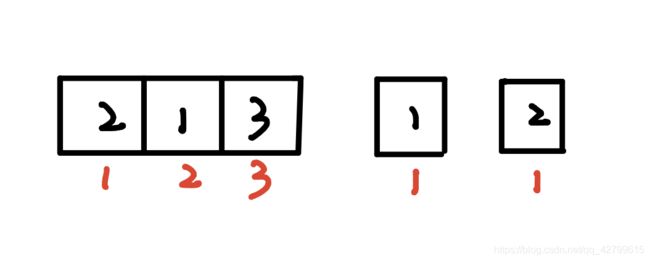
摆动序列的长度是不固定的,m为3的时候我们还可以自己凑出来,但是序列的长度如果为几十,几百呢?那可凑不出来了。
序列的长度为m,可以选择的数字的范围为[1,n]。最朴素的想法应该就是一个一个去试错。我们把长度为m的序列想象成m个格子,每个格子可以放1~n之间的任意数字。注意放的时候需要满足摆动序列的条件即可。然后我们一层一层地进行遍历,当我们在第一个格子上放入了2以后,我们又在2 ~ n之间进行遍历,依次取值放入第二个格子,第一格子放了2,第二个格子的值只能放入比第一个格子的值小的数字,在这里自然只能放1,然后到第三个格子,又开始依次判断1 ~ n之间的数字是否能放进去。直到遍历到第m个格子的时候,就说明找到了一个可能性,然后记录下来。
这样的时间复杂度取决于m的大小,m不是很大还好,但是当m的数量为几十,甚至几百的时候,这样的时间复杂度是可怕的。如果要用递归来做的话,递归的深度最深可以达到一千层。对于Java来说,递归的调用栈最深也不超过五十,如果要达到几百甚至一千的递归深度,那还是尽早放弃这种方法为好。
动态规划=动态递推
思考
然后我们就开始动动脑筋,既然是算法题,不可能说没有任何规律可言。要使长度为m的序列满足摆动序列的条件,我们只需要每次往第i个格子放数字的时候进行一下判断:若当前是偶数项,就得保证当前项的值小于前一项。(当前项是偶数项,前一项肯定是奇数项)。若当前项是奇数项,就得保证当前项的值一定要大于前一项。
序列的长度m可能会很大,但是我们不用关心m的长度,我们只需要每次放入一个值的时候判断一下,判断需要放入的值s[i]和前一项s[i - 1]的关系,若关系满足,则可以放入。不用关心整个序列,只用聚焦当前项和前一项即可。这时候自然回想:如果这两者之间有什么关系该多好。
如下图所示,当我们往第三个格子放入x以后,截止到当前的第三个格子,此时能组成多少种合法的摆动序列?当前项放入x已经固定,但是前一项的取值却不固定。由于第三项是奇数项,则前一项的值要小于当前项,所以前一项的取值范围为:1 ~ x-1。对于奇数项:我们若是知道当前项取值为x的时候,截止到前一项的所有合法的序列的数目为y1,那么截止到当前项,在当前项取值为x的情况下,所能组成的合法摆动序列的数目y = y1。同样的对于前一项,当前一项取值为[1,x-1]的时候,前一项所能组成的合法序列的数目,也应该分开来看。
有些人可能一下子不适应这种思考方式,让我们接着慢慢来看。
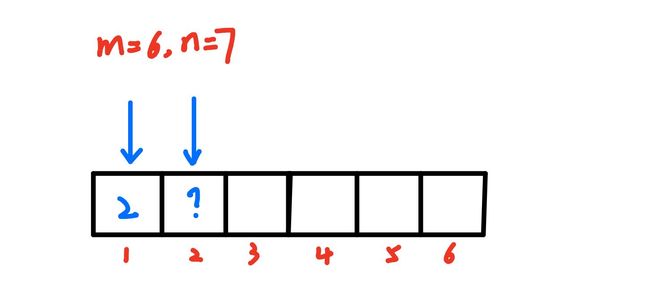
如下图所示,m=6,n=7,我要求的应该是长度为6的摆动序列的数目,你求长度为3,求长度为4的摆动序列的数目干甚?别急,这就是动态规划的精髓。我要求长度为6的摆动序列的数目,那么当我求出长度为5的摆动序列的数目以后我累加一下便是长度为6的,同理求长度为5的我得先知道长度为4的摆动序列的数目。一句话:决定你当前的是你的昨天或者是你的明天。
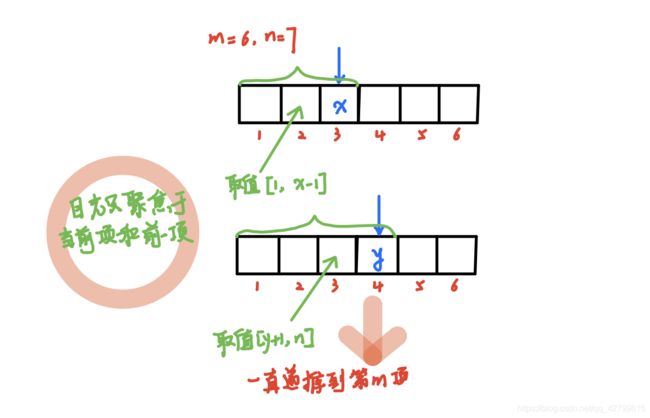
如果上面说的还是不好理解,我们再看这个图。
当前项为奇数项,且取值为x。当前项为奇数项,前一项为偶数项,取值范围为[1,x-1]。若我们能求出前一项取值为1的时候,截止到前一项所能组成的合法序列的数目S1;当前一项取值为2的时候,截止到前一项所能组成的合法序列的数目S2,一直到前一项为取值为x-1的时候,能组成的合法序列的数目为Sn我们都求出来了。那么对于当前项取值为x的时候,截止到当前项所能组成的合法的序列的数目应该为:S=S1+S2+S3…+Sn。
然后这样递推下去,直到当前项为第m项。
对应到这个图,我们求的是什么?求的是x往下延伸到第一项的所有分支的数目。
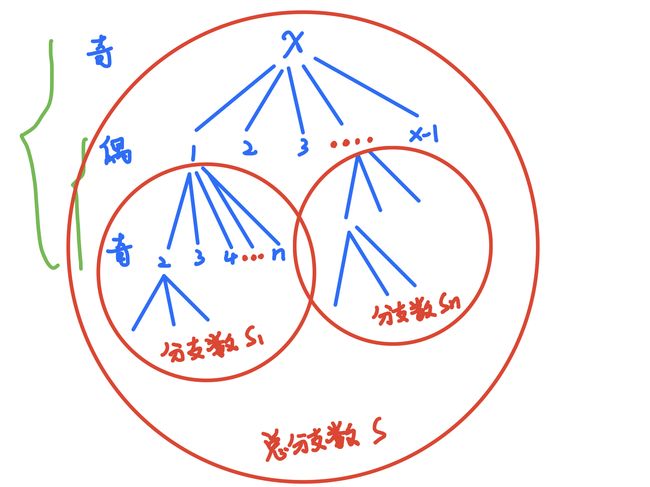
我只分析了奇数项,偶数项也是如此,只是取值范围有些不同。当前项为偶数项,且取值为x的时候,前一项的取值范围为[x+1,n]。
如果到这里都还能明白的话,那动态规划的解法你也就会了。动态规划说白了就是动态递推。我们只要搞清楚一个值和另一个值的关系,一直这样递推下去就能得到最终的解答。动态规划的英文为Dynamic Programming。翻译为动态编程都还好,翻译为动态规划就给人太玄乎的感觉,好像就是高瞻远瞩的感觉,但其实相反,动态规划关心的是局部,而不是一上来就是看整体。
动态规划的例题
爬楼梯
编程解决
代码一(未优化)
思考
只要懂了动态规划的思想,这个题目我们就可以开始干了。
若当前项取值为x,我们要求出截止到当前项为止能组成的摆动序列的数目,要求出截止到当前,我们要看的是到前一项能组成的摆动序列的数目。对于任一项,我们应该得知这些信息:对于长度为m的序列而言当前项是第几项,然后当前项的取值是多少,当前项的取值为x时能组成的合法的摆动序列的数目。只有这样才能一步一步地推下去,直到推到最后一项。
所以,对于任意一项,起码需要保存三个信息。当前项的位置(坐标i),当前项的取值x,以及当前取值为x时能组成的合法的摆动序列的数目。一般来说存数据,都是用数组。
我们看看,对于一维数组而言,任何一个数组a[i]只能保存或者对应两个信息:当前坐标i,当前坐标下保存的数据a[i],这充其量也就只能保存两种信息。
而二维数组呢?
对于a[i][j]。横坐标可以算一个信息,纵坐标可以算一个信息,横纵坐标对应的值a[i][j]也可以算是一种信息。刚好三种,这就挺合适的。
对应到我们的这个题目:我们建立一个二维数组dp[i][j](dp为动态规划的英文缩写):i可以表示当前项是对于长度为m的序列而言是第几项,j可以表示当前项取值为j,dp[i][j]表示当前项取值为j时能组成的合法序列的数目(截止到第i项)。对于长度为m的序列,我们只需要保证任意两项都满足摆动序列的定义,那么整个序列一定也是一个合法的摆动序列。
在这里,有个小问题,对于序列而言,我们是从1开始计数的,第1项,第2项,第3项,但是对于数组,我们是从0开始计数的。为了一一对应,我们的数组也可以从1开始计数。而j表示的是第i项的取值,n的取值范围为1~n,所以纵坐标也是从1开始的,最大值为n,而若建立的数组只是n列的话,只能到n-1。
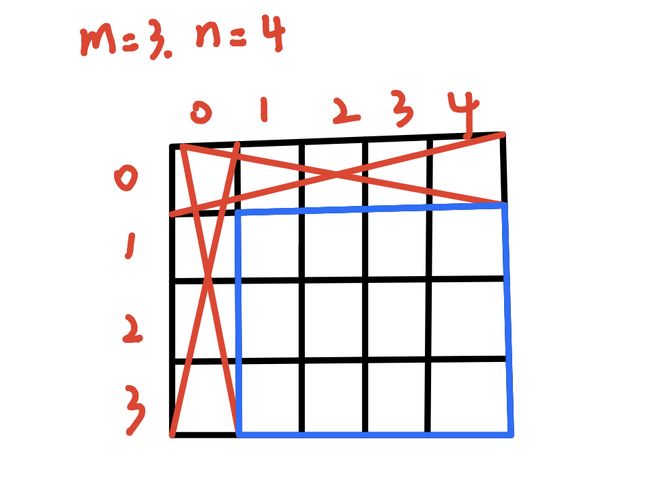
所以,如果要求的序列的长度为m,取值范围为n,那么我们可以建立一个m+1行,n+1列的数组。如下图所示,第一行和第一列空着,我们所使用的数组范围就是蓝色方框的范围。
 ](https://imgchr.com/i/JqsvHx)
](https://imgchr.com/i/JqsvHx)
这样的做法叫做动态规划(Dynamic Programming),所以建立的数组可以为dp[m+1][n+1]。dp[i][j]代表的意义一定要明白,这是做题的基础。
对于dp[1][2],i=1表示当前项位于序列的第一项,j=2表示第一项的取值为2。dp[1][2]表示当第1项取值为2的时候,截止到当前位置,能组成的合法的摆动序列数目。如果不太明白,可以回过头去看那幅分叉的树状图。
对于第一项,比较特殊。也就是数组的第二行,我们该怎么填?第一项为奇数项,由于它前面什么都没有,也就是说在1 ~ n的范围内可以随便取。由于它前面没有什么元素,有且仅为一项,所以dp[1][j]只能组成一种合法的摆动序列。
但是这里有个小问题,比如对于dp[1][1],表示第一项取值为1,如果序列的长度为1,这是没有任何问题的,但是一旦序列的长度大于1,比如2,由于第二项为偶数项,需要比第一项的值小,但是第一项为1也就是最小值,第二项是不可能再比第一项小,所以这种可能从一开始就被否定了。在这里我取值为0。
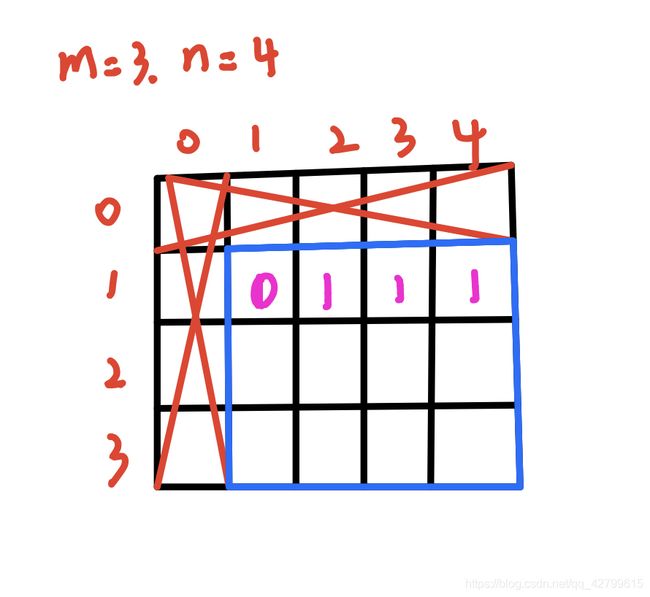
第二项是偶数项,前一项为奇数项。偶数项要小于奇数项。偶数项取值x,奇数项能取值的范围为[x+1,n]。第二项为1,也就是对于dp[2][1],前一项能取值的范围为[2,n]这里的n为4,也就是说有三种取法,即2,3,4。而对于前一项而言,当前一项取值为2的时候,它的可能性的数目则是由它的前一项来决定的。
代码
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int m = input.nextInt();
int n = input.nextInt();
input.close();
if (m == 1) {
System.out.println(n);
return;
}
int[][] dp = new int[m + 1][n + 1];
for (int j = 1; j <= n; ++j) {
if (j == 1) {
dp[1][j] = 0;
} else {
dp[1][j] = 1;
}
}
for (int i = 2; i <= m; ++i) {
// 当为奇数行时
// 有的人喜欢用i & 1来判断奇偶,对于java来说,这样倒是没啥必要,因为编译器还是挺智能的,不会一个一个地去取模来判断奇偶
if ((i % 2) == 1) {
for (int j = 1; j <= n; ++j) {
for (int k = 1; k < j; ++k) {
// 累加,求出dp[i][j]
dp[i][j] = (dp[i][j] + dp[i - 1][k]) % 10000;
}
}
} else {
for (int j = 1; j <= n; ++j) {
for (int k = j + 1; k <= n; ++k) {
dp[i][j] = (dp[i][j] + dp[i - 1][k]) % 10000;
}
}
}
}
int sum = 0;
for (int j = 1; j <= n; ++j) {
sum += dp[m][j];
}
System.out.println(sum);
}
代码二(优化)
思考
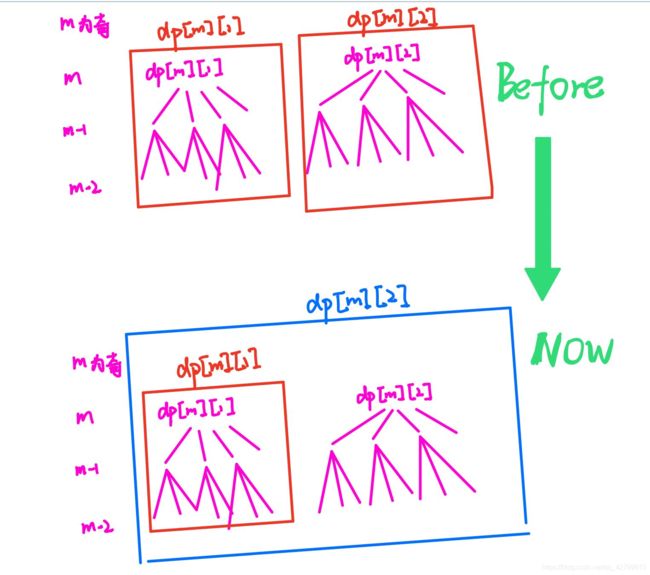
看到上面那个代码,三个嵌套的for循环,先不论时间复杂度,这个代码说实在的性能非常堪忧。这不比最初摒弃的那个暴力求解的方法好多少。
为什么呢?求dp[2][1]我们的使用一个for循环累加dp[1][2]到dp[1][4]的值。
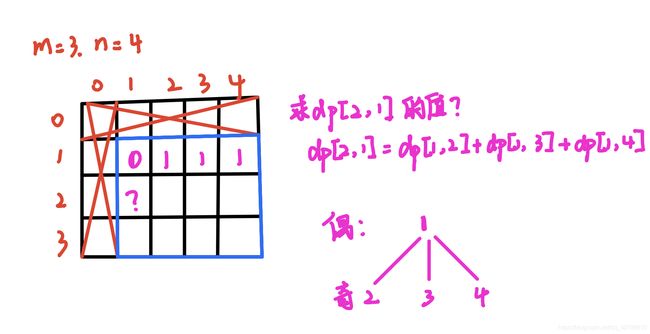
如果,这么看不清楚,我们看下面这个图:
若当前项为奇数项:
对于dp[i][j]我们好不容易遍历了一遍dp[i-1][1]到dp[i-1][j-1]的值求出了dp[i][j]但是到了dp[i][j+1],我们又要进行一次遍历。看下面这幅图就可以知道,对于dp[i][j+1],其实就多了dp[i-1][j],我们求dp[i][j+1]只需要dp[i][j] + dp[i-1][j]即可。
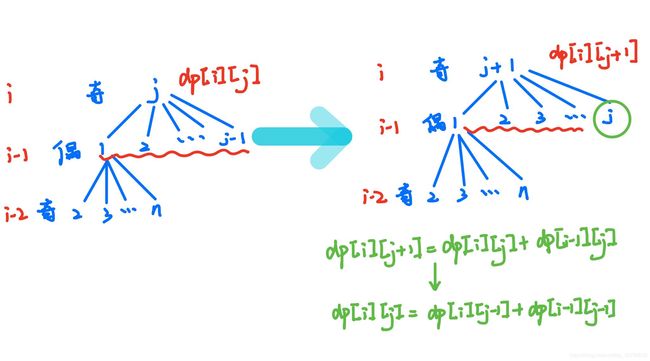
因此对于奇数项,我们便得到了这个公式:
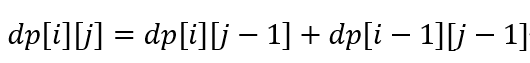
对于偶数项:我们可以看到dp[i][j+1]只是比dp[i][j]少了一个dp[i-1][j+1]。
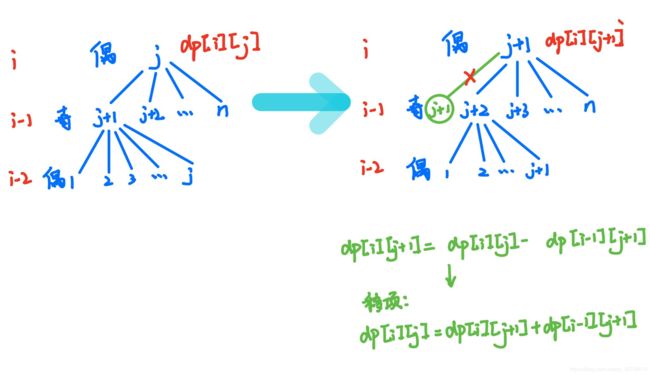
对于偶数项,又得到这个的递推公式:
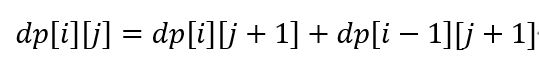
得到了这两个递推公式,在动态规划里面通常也叫状态转移方程,为什么要叫状态转移方程呢?状态方程通常是值如何通过前一项或者是后一项得到当前项,也就是如何由一个状态变为另一个状态。只有这样,我们才能一环扣一环地递推下去,得到最终结果。到了这一步:我才能真正好意思说我这个是动态规划了,看起来就没代码一那么糟糕了。
然后这里有个小技巧,对于奇数项,我们顺着递推就行,因为当前项是由上一项决定的。for循环从前往后遍历。
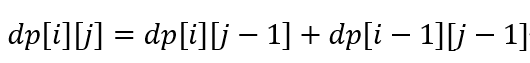
对于偶数项,当前项是由下一项决定的,for循环从后往前遍历。
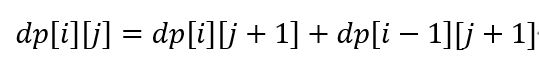
代码
public static void main(String[] args) {
Scanner input = new Scanner(System.in);
int m = input.nextInt();
int n = input.nextInt();
if (m == 1) {
System.out.println(n);
return;
}
int[][] dp = new int[m + 1][n + 1];
// 第一项为奇数项
for (int j = 1; j <= n; ++j) {
if (j == 1) {
dp[1][j] = 0;
} else {
dp[1][j] = dp[1][j - 1] + 1;
}
}
for (int i = 2; i <= m; ++i) {
//奇数
if ((i % 2) == 1) {
for (int j = 2; j <= n; ++j) {
dp[i][j] = (dp[i][j - 1] + dp[i - 1][j - 1]) % 10000;
}
} else {
for (int j = n - 1; j >= 1; --j) {
dp[i][j] = (dp[i][j + 1] + dp[i - 1][j + 1]) % 10000;
}
}
}
// 对比看下面的图,就知道为什么这里要判断m是奇数,还是偶数了
int ans = ((m % 2) == 1) ? dp[m][n] : dp[m][1];
System.out.println(ans);
}
注意点
代码可能不好理解,请继续往下看
还有一些需要注意的点。对于偶数项而言,当处于最后一列,也就是dp[i][n](这里的i为偶数),此时表示当前项为最大值n,不可能比前一项小,因此当前项为n的时候,所能组成的合法的序列数为0。而数组初始化的时候全部都为0,我们就不用刻意令其为0。
对于奇数项而言,当处于第1列,也就是处于dp[i][1]的位置时(这里的i为奇数),此时表示当前项为1,也就是最小值,不可能大于前一项,因此当该项取值为1的时候,不可能有合法的序列,因此为0。
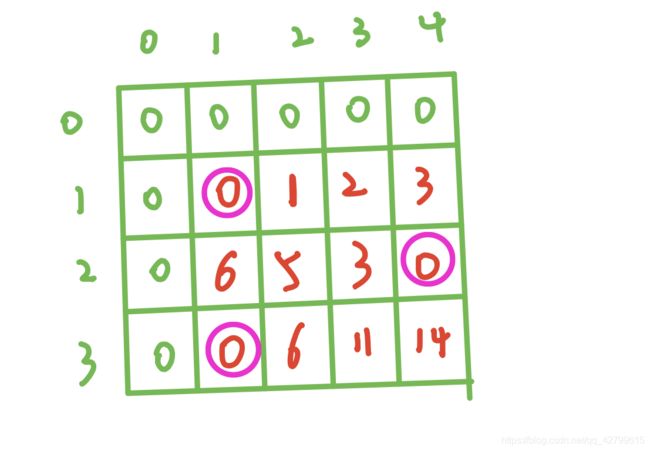
而第一行的初始化则变为了:0,1,2,3.这可能不好理解。
为什么是0,1,2,3呢。dp[1][1]为0还好理解,因为第一项为1,除非序列长度为1,不然肯定是不合法的。dp[1][2]表示第一项的取值只有为2这么一种情况,而dp[1][3]则表示第一项取值小于等于三有两种情况,取值为2,取值为3。因此我们可以发现dp[i][j]的值发生了一点潜移默化的改变。
对于奇数项:dp[i][j]表示对于第i项,当前项的值小于等于j所能组成的合法序列的数量的总和。
对于偶数项:dp[i][j]表示对于第i项,当前项的值大于等于j所能组成的合法序列的数量的总和。
这不好理解,我们继续看图:
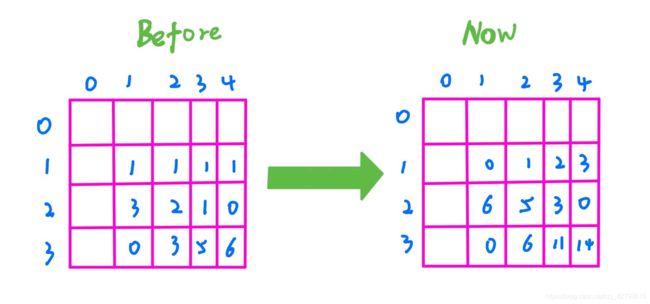
以m=3,n=4为例,我们看一下dp数组的变化,主要也在于我们对于偶数项遍历的方向进行了改变。
总结
什么是动态规划呢?
动态规划并不是高瞻远瞩,而是将目光放小,聚焦于当前项,前一项或者是后一项。要求出问题的最终答案,并不是一上来就开始解决,而是先将其分解为一个个子问题,通过解决一个一个地子问题,最终就解决了一个大问题。比如,你说你要考上清华,你整天都在那里想我要上清华,我要上清华,这是不行的。对于高中生而言,考上清华需要你不偏科,语数外,物化生,你都要好好学。把学习成绩搞上去,把基础打牢。然后呢,考试的时候要细心,要沉着冷静。还有呢,你的身体得养好,该补的营养补上,该锻炼要锻炼,身体扎实,学习才有劲头。你只有把这一个一个的子问题解决掉,最终才能考上清华,解决这个大问题。
动态规划的题目也是:不要一上来就聚焦于全局,而是想一下,我该怎么从第一步开始往下走,一步一步走下去,最终走到终点。而这就是寻找状态转移方程的过程。我只要能知道如何由下一步走到当前这一步,或者是如何由上一步走到当前这一步,一环扣一环地走下去,一定能到达终点。
结束语
到此,这个题便结束了,不知不觉洋洋洒洒写了这么多,最初只是想记录一下自己做题的想法。真正写下来却发现字数还真不少。而对于动态规划,其实还有很多可以说的,我也争取多总结一些动态规划的题目出来,这对于提升自己的编程能力,算法功底,甚至是对于面试都会有不小的帮助。下期再见。