矩阵乘法学习记录+模板+例题
学习记录主讲矩阵乘法(原理、计算、功能、应用)
模板为矩阵乘法和矩阵快速幂的C++代码实现
例题为矩阵快速幂求斐波那契数和一个ACM的具体题目(用矩阵快速幂优化概率DP)
学习记录:
(from :http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html)
看个例子:
![]()
计算规则:
第一个矩阵第一行的每个数字(2和1),各自乘以第二个矩阵第一列对应位置的数字(1和1),
然后将乘积相加( 2 x 1 + 1 x 1),得到结果矩阵左上角的那个值3。
用代码显示就是:
/*
假设 A 是 m*p 的矩阵 , B 是 p*n 的矩阵
记 C = AB (C 是 矩阵 A与B的乘积)
那么 C 是 m*n 的矩阵
*/
for (int i = 1;i <= m;++i)//A的行
{
for (int j = 1;j <= n;++j)//B的列
{
for (int k = 1;k <= p;++k)//通过公式求C
{
C[i][j] += A[i][k]*B[k][j];
}
}
} ![]()
也就是说,结果矩阵第m行与第n列交叉位置的那个值,等于第一个矩阵第m行与第二个矩阵第n列,对应位置的每个值的乘积之和。
有没有想过矩阵乘法为什么是这样的计算规则?
分享一篇文章(全英文):https://nolaymanleftbehind.wordpress.com/2011/07/10/linear-algebra-what-matrices-actually-are/
PS:作为一只英语渣渣 文章我是没看的 主要是看到高斯消元的时候恍然大悟,原来:
矩阵的本质就是线性方程式,两者是一一对应关系。(高斯消元就可以利用矩阵求解线性方程组)
看这样一组最简单的线性方程组:
![]()
它写成矩阵是这样:
![]()
利用解方程的原理再看矩阵乘法:系数矩阵第一行的2和1,各自与 x 和 y 的乘积之和,等于3。
严格的证明可以参考文首的链接。
当我们发现矩阵的本质就是线性方程式这个强大的规律,很多数学问题都可以用矩阵解决!
比如斐波那契数列 f[n] = f[n-1]+f[n-2] 就可以看做线性方程从而转换成矩阵
具体怎么做后面例题将会讲到。
然后很多(概率)dp的状态转移方程也可以看做线性方程组构造矩阵求解
高斯消元就更不用说,直接就是利用矩阵求解线性方程
1.直接求解矩阵的相关问题
2.矩阵和向量相关(向量混合积(叉乘)),可以求解同时对平面多个点的平移旋转翻转等问题
3.矩阵可以用来求解线性方程组(高斯消元)
4.许多数学题都可以通过构造矩阵求解
5.等等
具体题目:
http://www.cnblogs.com/DreamUp/archive/2010/07/27/1786225.html[此文讲解了矩阵应用的具体10个题目]
矩阵包含的知识太多,真心想弄懂还是认真学习线性代数
模板:
/*
假设 A 是 m*p 的矩阵 , B 是 p*n 的矩阵
记 C = AB (C 是 矩阵 A与B的乘积)
那么 C 是 m*n 的矩阵
*/
for (int i = 1;i <= m;++i)//A的行
{
for (int j = 1;j <= n;++j)//B的列
{
for (int k = 1;k <= p;++k)//通过公式求C
{
C[i][j] += A[i][k]*B[k][j];
}
}
}#include
using namespace std;
typedef long long ll;
const int N = 2;
struct Matrix
{
ll mat[N][N];
};
Matrix operator * (Matrix a,Matrix b)
{
Matrix c;
for (int i = 0;i < N;++i)
{
for (int j = 0;j < N;++j)
{
c.mat[i][j] = 0;
for (int k = 0;k < N;++k)
{
c.mat[i][j] += a.mat[i][k]*b.mat[k][j];
}
}
}
return c;
}
Matrix operator ^ (Matrix a,ll k)//矩阵幂
{
Matrix c
for (int i = 0;i < N;++i)
{
for (int j = 0;j < N;++j)
{
c.mat[i][j] = (i==j);//初始化为单位矩阵
}
}
//据说任何矩阵乘以单位矩阵其值不会变
for (;k;k>>=1)
{
if (k&1) c = c*a;
a = a*a;
}
return c;
}
int main()
{
return 0;
} 例题(代码):
1.矩阵乘法求斐波那契数列
斐波那契数列:f[n] = f[n-1] + f[n-2]
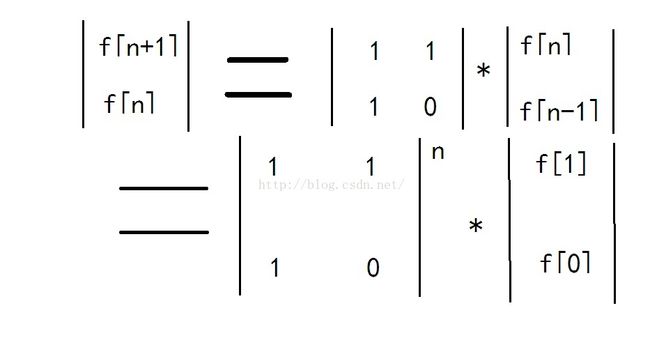
写这样两个等式:
(1)f[n] + (1)f[n-1] = f[n+1]
(1)f[n] + (0)f[n-1] = f[n]
括号内的数看做系数,f[n]等看做未知数
根据这另个等式和系数*未知数==等式右边,可以构造矩阵:
很显然的式子,系数*未知数==等式右边,不断递推就得到系数矩阵的n次方成上未知数等于等式右边
所以最后的答案f[n]就是矩阵matrix[0][1]位置的值
说说具体代码实现的细节:
首先,当n很大的时候,f[n]会很大,所以代码实现取了模
其次,当n很大的时候,算法会很慢,于是用矩阵快速幂
最后,使用结构体而非单纯二维数组是因为 :
1.结构体能被函数直接返回
2.结构体可以重载乘法等运算符,看着更清晰
代码实现:(测试)
#include
#include
#include
using namespace std;
typedef long long LL;
const LL mod = 1000000007;
/*
矩阵快速幂求斐波那契数列
输入 n 输出 f[n]
*/
struct Mat
{
LL mat[2][2];
};
Mat operator * (Mat a,Mat b)//矩阵乘法
{
Mat c;
for (int i = 0;i < 2;++i)
{
for (int j = 0;j < 2;++j)
{
c.mat[i][j] = 0;
for (int k = 0;k < 2;++k)
{
c.mat[i][j] = ((a.mat[i][k]*b.mat[k][j])%mod + c.mat[i][j])%mod;
}
}
}
return c;
}
Mat operator ^ (Mat a,LL k)//矩阵幂
{
Mat c;
for (int i = 0;i < 2;++i)
{
for (int j = 0;j < 2;++j)
{
c.mat[i][j] = (i==j);//初始化为单位矩阵
}
}
//据说任何矩阵乘以单位矩阵其值不会变
for (;k;k>>=1)
{
if (k&1) c = c*a;
a = a*a;
}
return c;
}
int main()
{
LL n;
while (cin>>n)
{
Mat a;
a.mat[0][0] = 1,a.mat[0][1] = 1,a.mat[1][0] = 1,a.mat[1][1] = 0;
Mat fn = a^n;
cout< 2.POJ 3744 Scout YYF I(概率DP矩阵快速幂优化)
#include
#include
#include
#include
using namespace std;
typedef long long ll;
struct Matrix
{
double mat[2][2];
};
Matrix operator * (Matrix a,Matrix b)
{
Matrix c;
for (int i = 0;i < 2;++i)
{
for (int j = 0;j < 2;++j)
{
c.mat[i][j] = 0;
for (int k = 0;k < 2;++k)
{
c.mat[i][j] += a.mat[i][k]*b.mat[k][j];
}
}
}
return c;
}
Matrix operator ^ (Matrix a,ll k)//矩阵幂
{
Matrix c;
memset(c.mat,0,sizeof(c.mat));
for(int i=0;i<2;i++)c.mat[i][i]=1;//初始化为单位矩阵
//据说任何矩阵乘以单位矩阵其值不会变
for (;k;k>>=1)
{
if (k&1) c = c*a;
a = a*a;
}
return c;
}
int x[111];
int main()
{
int n;double p;
while (cin>>n>>p)
{
for (int i = 0;i < n;++i) scanf("%d",x+i);
sort(x,x+n);
double ans = 1.0;
Matrix c;
c.mat[0][0] = p,c.mat[0][1] = 1.0-p;
c.mat[1][0] = 1.0,c.mat[1][1] = 0.0;
Matrix a = c^(x[0]-1);
ans *= (1-a.mat[0][0]);
for (int i = 1;i < n;++i)
{
if (x[i] == x[i-1]) continue;
a = c^(x[i]-x[i-1]-1);
ans *= (1.0-a.mat[0][0]);
}
printf("%.7f\n",ans);
}
return 0;
} 参考资料:
http://blog.csdn.net/thisinnocence/article/details/38641493?utm_source=tuicool&utm_medium=referral
http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html(学习部分基本全部摘抄自此文)