处女座算法之大整数乘法(从O(N^2)到O(N^1.59)的思想)
每次看算法的优化设计都会觉得:优化算法的人都是处女座!
《算法设计与分析》一书讲完分治之后顺手讲了大数乘法的分治递归算法,然后又兴冲冲地将原本O(N^2)的算法优化成O(N^1.59)
package com.mustso.java2;
import java.util.Scanner;
public class BigIntMultiply {
final static int base = 10;//十进制数
final static int N = 100;
public static String bigIntMultiply(String A,String B){
//首先考虑负数
int t = 0;
if (A.charAt(0)=='-'){
++t;
A = A.substring(1);
}
if (B.charAt(0)=='-'){
++t;
B = B.substring(1);
}
int [] C = new int[N];
/*
* 计数器i:B从个位向高位遍历
* 计数器j:A从个位向高位遍历
* 计数器k+l:数组C保存的结果,C[0]保存结果的个位
*/
for (int i = B.length()-1,k = 0;i >= 0;--i,++k){
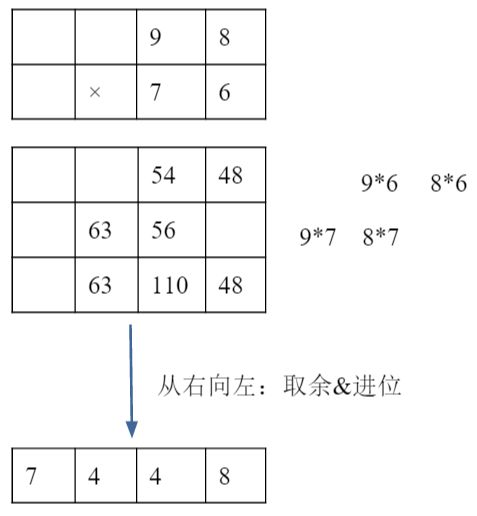
for (int j = A.length()-1,l = 0;j >= 0;--j,++l){
C[k+l]+=(int)(A.charAt(j)-'0')*(B.charAt(i)-'0');
}
}
/*
* 说明:一个a位数乘以一个b位数的结果只可能是(a+b)位数或(a+b-1)位数
* 比如:99*99 = 9801//2位数乘2位数最大是4位数
* 10*10 = 100 //2位数乘2位数最小是3位数
*/
//进位&取余
for (int i = 0;i < A.length()+B.length()-1;++i){
C[i+1]+=C[i]/base;
C[i]%=base;
}
String ans = "";
for (int i = 0;i < A.length()+B.length();++i){
ans = String.valueOf(C[i])+ans;
}
if (ans.equals("0")) return "0";
if (ans.charAt(0)=='0'){
ans = ans.substring(1);
}
if (t == 1){
ans = "-"+ans;
}
return ans;
}
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
while (cin.hasNext()){
String A = cin.next();
String B = cin.next();
System.out.println(bigIntMultiply(A,B));
}
}
}
若数字A的长度为a,数字B的长度为b,那么时间复杂度为O(a*b)
以前看到别人说过O(N^1.59)的算法,当时觉得很神奇很牛逼
仔细一看,其实就是将递归里面的4次递归算乘法改成3次
(那个矩阵乘法的优化算法也是用减少乘法次数,利用数学方法将原公式变形以减少乘法次数,也就是减少了递归的次数)
翻开算法设计与分析一书的第2.4节--“大整数的乘法”
它是这样说的:
设X、Y都是n位的二进制数,现在要计算它们的乘积XY
将n位二进制整数X和Y都分为2段,每段的长为n/2位(为简单起见,假设n是2的幂)

如果按此式计算XY必须进行四次n/2位整数的乘法(AC,AD,BC和BD),以及3次不超过2n位的整数加法(分别对应于式中的加号),此外还要进行2次移位(分别对应于式中乘2^n和乘2^(n/2))。所有这些加法和移位共用O(n)步运算。设T(n)是2个n位整数相乘所需的运算总数,则有:

我个人的感受是,那些优化算法的人都是处女座。(以后更是深有体会)
上述二进制大整数乘法同样可应用于十进制大整数的乘法提高算法效率。
比如1234×5678 =>(12×10^2+34)×(56×10^2+78)
大致算法实现如下:
package com.mustso.java1;
import java.util.Scanner;
public class BigIntMultiply {
final static int size = 4;//设置可以直接计算的位数
public static String bigIntMultiply(String X,String Y){
int len = Math.max(X.length(), Y.length());
//补齐X、Y,使之长度相同
X = formatLength(X,len);
Y = formatLength(Y,len);
//少于size位的数可以直接计算不会溢出
if (len <= size){
return ""+(Integer.parseInt(X)*Integer.parseInt(Y));
}
//将X、Y对半分
int mid = len/2;
String A = X.substring(0, mid);
String B = X.substring(mid);
String C = Y.substring(0, mid);
String D = Y.substring(mid);
//分治思想,递归求解
String AC = bigIntMultiply(A,C);
String AD = bigIntMultiply(A,D);
String BC = bigIntMultiply(B,C);
String BD = bigIntMultiply(B,D);
//处理BD,得到原位及进位
String[] newBD = jinweiString(BD,len-mid);
//处理AD+BC的和
String ADBC = bigAddition(AD,BC);
//加上BD的进位
if (!newBD[1].equals("0")){
ADBC = bigAddition(ADBC,newBD[1]);
}
//得到ADBC的进位
String[] newADBC = jinweiString(ADBC,len-mid);
//AC+ADBC的进位
AC = bigAddition(AC,newADBC[1]);
//最终结果
return AC+newADBC[0]+newBD[0];
}
/*
* 处理数字串,分离出进位;
* str[0]为原位数字,str[1]为进位
*/
public static String[] jinweiString(String X,int len){
String []str = {X,"0"};
if (len < X.length()){
int t = X.length()-len;
str[1] = X.substring(0, t);
str[0] = X.substring(t);
}
else {
//要保证结果的length与形参len一致,不足则高位补零
String ans = str[0];
for (int i = ans.length();i < len;++i){
ans = "0"+ans;
}
str[0] = ans;
}
return str;
}
public static String bigAddition(String X,String Y){
int len = Math.max(X.length(), Y.length());
X = formatLength(X,len);
Y = formatLength(Y,len);
int jinwei = 0;
String ans = "";
//按位从后往前加
for (int i = len-1;i>=0;--i){
int t = jinwei+Integer.parseInt(X.substring(i, i+1))
+Integer.parseInt(Y.substring(i, i+1));//charAt(i)
if (t>9){
//超过9就进位并取余保留个位
jinwei = t/10;
t %= 10;
}
else{
jinwei = 0;
}
//拼接结果字符串
ans = ""+t+ans;
}
while (jinwei!=0){
ans = ""+jinwei%10+ans;
jinwei/=10;
}
return ans;
}
public static String formatLength(String X,int len){
while (X.length()测试:
说明:
大数减法比较麻烦,所以第二种代码暂时不支持负数。
同理(A-B)、(D-C)也是用减法,所以暂时没有实现。
所以总体而言我写的第二种算法是不合格的,时间复杂度还是O(n^2),后期可能直接就用java大数去优化吧(或者哪天抽了写个大数减法?)
目前先这样。。。
参考文献:
《算法设计与分析》