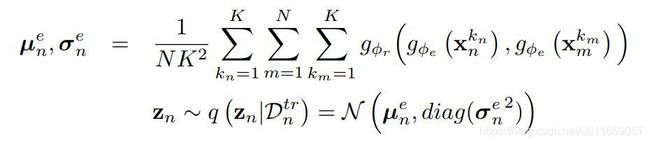Meta-Learning with Latent Embedding Optimization
LEO 思想
这是 DeepMind 写的关于 Meta Learning 的一篇文章。MAML 虽然可以通过少量梯度下降就能找到适应新任务的最优参数，然而对 extreme low-data regimes 在高维参数空间上操作时，还是过于不便。而 LEO 则通过学习关于模型参数的 a data-dependent latent generative representation，并在这种低维的 latent space 中执行基于梯度下降，可以一定程度上绕过这些痛点。LEO 算法能够捕获数据中的不确定性，将基于梯度的自适应优化过程，从模型参数的高维空间中分离出来，并通过实验证明了这种方法是可行且有益的。
LEO 的算法示意图
如下图所示，LEO 没有像 MAML 那样显式维护模型参数 
，而是以输入数据为条件，学习模型参数的生成分布。即，不再寻找单个最优解 
，而是在 
上逼近依赖于数据的条件概率分布（data-dependent conditional probability distribution），这种条件更宽松，也更具有表现力。
LEO 伪代码
首先给定一个任务实例 
，输入样本 
通过编码器生成一个 latent code 
，然后使用参数生成器将其解码为参数 
。在 latent space 中使用一个或多个自适应步骤，通过对 的损失进行计算，采取梯度下降后得到新的 
，再次解码出新的模型参数，并获得新的损失。最后，对最终的 latent code 进行解码，产生最终的自适应参数 
，该参数可用于计算特定任务的元损失。
网络的总体结构
编码器确保在初始 latent code 和参数已经与数据相关。考虑到实例中所有类之间的成对关系，编码过程还利用了关系网络，允许 latent code 是的 context-dependent 的。直观地说，相似类之间细粒度区分所需的决策边界，可能需要不同于更广泛分类所需的决策边界。其中解码器类似于生成模型，从低维 latent code 映射到模型参数的分布。
编码阶段
首先，对问题实例 
中的每个样本，由编码器网络 
映射到 intermediate hidden-layer code space 
中的 code。然后，对应于不同训练样本在的 中的 code 成对地连接（在 K-shot 的情况下导致 
对 pair）并由关系网络 处理。 个输出按类分组，并在每组内取平均值，得到低维空间中 
概率分布的 
参数（其中对于每个了类别 
）。
给定类别 n 的 K 个样本 
，编码器 
和关系网络 
共同将具有 class-conditional 的对角协方差的条件多元高斯分布参数化，可以从中采样以输出一类相关的 latent code 
：
编码器和关系网络定义了从一个或多个类实例到与该类对应的 latent space 
中的 latent code 
之间的随机映射。最终的 latent code 可以通过每个类别 i 的 latent code 
进行 concate 操作来获得：![z=[z_{1},z_{2},\cdots ,z_{n}]](http://img.e-com-net.com/image/info8/1a2535d2ca4a41f19f3ddafab43570e1.gif){kind=small}
。
解码阶段
使用 class-specific 的 latent code 来生成分类器的顶层权重。其中，
是一个 N-way 的线性 softmax 分类器，模型参数 
，每个 
可以是原始输入，也可以是一些特征。然后，给出 latent code 
， 解码器函数 
用于参数化模型参数空间 中具有对角协方差的高斯分布，从中采样与 class-dependent 的参数 
：
也就是说，使用解码器 
将 
独立地映射到 softmax 分类器的顶层参数 ，该解码器本质上是模型参数的随机生成器。
损失函数
给定解码后的参数，使用交叉熵函数定义 inner loop 的分类损失：
解码器 是 latent space 和高维模型参数空间 之间的可微映射。 latent code 相对于训练损失的优化为 
。解码器 将每个自适应步骤的自适应 latent code 
转换为有效的模型参数 
。此外，通过解码器反向传播错误，编码器和关系网可以学习提供数据条件 latent code z，该编码 z 为分类器模型生成适当的初始化点 。
初始化和自适应过程产生一个新的分类器 
，在 out loop 中对该任务的验证集 
进行评估。元训练通过最小化以下目标函数，来更新编码器、关系和解码器网络参数：
式中 
。与《Beta-VAE: Learning basic visual concepts with a constrained variational framework》中定义的损失类似，使用加权 KL 散度项来调整 latent space，并鼓励生成模型学习分离嵌入，这也应通过移除潜在空间梯度维度之间的相关性来简化LEO 的 inner loop。式中第三项使得编码器和关系网输出接近于自适应代码的参数初始化，从而尽可能减少自适应过程的负载。
代码
代码只贴了 model 部分，作者用 TensorFlow + sonnet 写的，自己标注了每个张量的维度，方便自己复习巩固。
class LEO(snt.AbstractModule):
"""Sonnet module implementing the inner loop of LEO."""
def __init__(self, config=None, use_64bits_dtype=True, name="leo"):
super(LEO, self).__init__(name=name)
self._float_dtype = tf.float64 if use_64bits_dtype else tf.float32
self._int_dtype = tf.int64 if use_64bits_dtype else tf.int32
self._inner_unroll_length = config["inner_unroll_length"]
self._finetuning_unroll_length = config["finetuning_unroll_length"]
self._inner_lr_init = config["inner_lr_init"]
self._finetuning_lr_init = config["finetuning_lr_init"]
self._num_latents = config["num_latents"]
self._dropout_rate = config["dropout_rate"]
self._kl_weight = config["kl_weight"] # beta
self._encoder_penalty_weight = config["encoder_penalty_weight"] # gamma
self._l2_penalty_weight = config["l2_penalty_weight"] # lambda_1
# lambda_2
self._orthogonality_penalty_weight = config["orthogonality_penalty_weight"]
assert self._inner_unroll_length > 0, ("Positive unroll length is necessary"
" to create the graph")
def _build(self, data, is_meta_training=True):
"""Connects the LEO module to the graph, creating the variables.
Args:
data: A data_module.ProblemInstance constaining Tensors with the
following shapes:
- tr_input: (N, K, dim)
- tr_output: (N, K, 1)
- tr_info: (N, K)
- val_input: (N, K_valid, dim)
- val_output: (N, K_valid, 1)
- val_info: (N, K_valid)
where N is the number of classes (as in N-way) and K and the and
K_valid are numbers of training and validation examples within a
problem instance correspondingly (as in K-shot), and dim is the
dimensionality of the embedding.
is_meta_training: A boolean describing whether we run in the training
mode.
Returns:
Tensor with the inner validation loss of LEO (include both adaptation in
the latent space and finetuning).
"""
if isinstance(data, list):
data = data_module.ProblemInstance(*data)
self.is_meta_training = is_meta_training
self.save_problem_instance_stats(data.tr_input)
# encoder only calculate train_data
# latents: ( ways, shots, 64 ), KL: some number
latents, kl = self.forward_encoder(data)
# tr_loss: ( ways, shots ), adapted_classifier_weights: ( ways, shots, 640 )
tr_loss, adapted_classifier_weights, encoder_penalty = self.leo_inner_loop(
data, latents)
# val_loss: ( ways, query_sample )
val_loss, val_accuracy = self.finetuning_inner_loop(
data, tr_loss, adapted_classifier_weights)
val_loss += self._kl_weight * kl
val_loss += self._encoder_penalty_weight * encoder_penalty
# The l2 regularization is is already added to the graph when constructing
# the snt.Linear modules. We pass the orthogonality regularizer separately,
# because it is not used in self.grads_and_vars.
regularization_penalty = (
self._l2_regularization + self._decoder_orthogonality_reg
)
batch_val_loss = tf.reduce_mean(val_loss)
batch_val_accuracy = tf.reduce_mean(val_accuracy)
return batch_val_loss + regularization_penalty, batch_val_accuracy
@snt.reuse_variables
def leo_inner_loop(self, data, latents): # latents: ( ways, shots, 64 )
with tf.variable_scope("leo_inner"):
inner_lr = tf.get_variable(
"lr", [1, 1, self._num_latents],
dtype=self._float_dtype,
initializer=tf.constant_initializer(self._inner_lr_init))
starting_latents = latents
loss, _ = self.forward_decoder(data, latents) # loss: ( ways, shots ), _: ( ways, shots, 640 )
for _ in range(self._inner_unroll_length):
loss_grad = tf.gradients(loss, latents) # dLtrain/dz
latents -= inner_lr * loss_grad[0]
loss, classifier_weights = self.forward_decoder(data, latents) # loss: ( ways, shots ), classifier_weights: ( ways, shots, 640 )
if self.is_meta_training:
encoder_penalty = tf.losses.mean_squared_error(
labels=tf.stop_gradient(latents), predictions=starting_latents)
encoder_penalty = tf.cast(encoder_penalty, self._float_dtype)
else:
encoder_penalty = tf.constant(0., self._float_dtype)
return loss, classifier_weights, encoder_penalty # loss: ( ways, shots ), classifier_weights: ( ways, shots, 640 )
@snt.reuse_variables
def finetuning_inner_loop(self, data, leo_loss, classifier_weights):
# leo_loss: ( ways, shots ), classifier_weights: ( ways, shots, 640 )
# tr_loss: ( ways, shots )
tr_loss = leo_loss
with tf.variable_scope("finetuning"):
finetuning_lr = tf.get_variable(
"lr", [1, 1, self.embedding_dim],
dtype=self._float_dtype,
initializer=tf.constant_initializer(self._finetuning_lr_init))
for _ in range(self._finetuning_unroll_length):
loss_grad = tf.gradients(tr_loss, classifier_weights)
classifier_weights -= finetuning_lr * loss_grad[0]
# tr_loss: ( ways, shots )
tr_loss, _ = self.calculate_inner_loss(data.tr_input, data.tr_output,
classifier_weights)
# val_loss: ( ways, query_sample )
val_loss, val_accuracy = self.calculate_inner_loss(
data.val_input, data.val_output, classifier_weights)
return val_loss, val_accuracy
@snt.reuse_variables
def forward_encoder(self, data):
# encoder_outputs: ( ways, shots, 64 )
encoder_outputs = self.encoder(data.tr_input)
# relation_network_outputs: ( ways, shots, 2 * 64 )
relation_network_outputs = self.relation_network(encoder_outputs)
# latent_dist_params: ( ways, shots, 2 * 64 )
latent_dist_params = self.average_codes_per_class(relation_network_outputs)
# latents: ( ways, shots, 64 ), KL: some number
latents, kl = self.possibly_sample(latent_dist_params)
return latents, kl
@snt.reuse_variables
def forward_decoder(self, data, latents): # latents: ( ways, shots, 64 )
# weights_dist_params: ( ways, shots, 2 * 640 )
weights_dist_params = self.decoder(latents)
# Default to glorot_initialization and not stddev=1.
fan_in = self.embedding_dim.value
fan_out = self.num_classes.value
stddev_offset = np.sqrt(2. / (fan_out + fan_in))
classifier_weights, _ = self.possibly_sample(weights_dist_params, # classifier_weights: ( ways, shots, 640 )
stddev_offset=stddev_offset)
tr_loss, _ = self.calculate_inner_loss(data.tr_input, data.tr_output,
classifier_weights) # tr_loss: ( ways, shots )
return tr_loss, classifier_weights # tr_loss: ( ways, shots ), classifier_weights: ( ways, shots, 640 )
@snt.reuse_variables
def encoder(self, inputs):
with tf.variable_scope("encoder"):
after_dropout = tf.nn.dropout(inputs, rate=self.dropout_rate)
regularizer = tf.contrib.layers.l2_regularizer(self._l2_penalty_weight)
initializer = tf.initializers.glorot_uniform(dtype=self._float_dtype)
encoder_module = snt.Linear(
self._num_latents,
use_bias=False,
regularizers={"w": regularizer},
initializers={"w": initializer},
)
outputs = snt.BatchApply(encoder_module)(after_dropout)
return outputs
@snt.reuse_variables
def relation_network(self, inputs):
# inputs is encoder_outputs: ( ways, shots, 64 )
with tf.variable_scope("relation_network"):
regularizer = tf.contrib.layers.l2_regularizer(self._l2_penalty_weight)
initializer = tf.initializers.glorot_uniform(dtype=self._float_dtype)
relation_network_module = snt.nets.MLP(
[2 * self._num_latents] * 3,
use_bias=False,
regularizers={"w": regularizer},
initializers={"w": initializer},
)
total_num_examples = self.num_examples_per_class * self.num_classes
# inputs: ( ways * shots, 64 )
inputs = tf.reshape(inputs, [total_num_examples, self._num_latents])
# left: ( ways * shots, ways * shots, 64 )
"""
like:
[[1,1,1], [2,2,2]] => [[[1,1,1], [1,1,1]], [[2,2,2], [2,2,2]]]
"""
left = tf.tile(tf.expand_dims(inputs, 1), [1, total_num_examples, 1])
# right: ( ways * shots, ways * shots, 64 )
"""
like:
[[1,1,1], [2,2,2]] => [[[1,1,1], [2,2,2]], [[1,1,1], [2,2,2]]]
"""
right = tf.tile(tf.expand_dims(inputs, 0), [total_num_examples, 1, 1])
# concat_codes: ( ways * shots, ways * shots, 128 )
concat_codes = tf.concat([left, right], axis=-1)
# outputs: ( ways * shots, ways * shots, 128 )
outputs = snt.BatchApply(relation_network_module)(concat_codes)
# outputs: ( ways * shots, 128 )
outputs = tf.reduce_mean(outputs, axis=1)
# 2 * latents, because we are returning means and variances of a Gaussian
# outputs: ( ways, shots, 128 )
outputs = tf.reshape(outputs, [self.num_classes,
self.num_examples_per_class,
2 * self._num_latents])
return outputs
@snt.reuse_variables
def decoder(self, inputs): # inputs: ( ways, shots, 64 )
with tf.variable_scope("decoder"):
l2_regularizer = tf.contrib.layers.l2_regularizer(self._l2_penalty_weight)
orthogonality_reg = get_orthogonality_regularizer(
self._orthogonality_penalty_weight)
initializer = tf.initializers.glorot_uniform(dtype=self._float_dtype)
# 2 * embedding_dim, because we are returning means and variances
decoder_module = snt.Linear(
2 * self.embedding_dim,
use_bias=False,
regularizers={"w": l2_regularizer},
initializers={"w": initializer},
)
outputs = snt.BatchApply(decoder_module)(inputs)
self._orthogonality_reg = orthogonality_reg(decoder_module.w)
return outputs # ( ways, shots, 2 * 640 )
def average_codes_per_class(self, codes):
# params codes is latent_dist_params: ( ways, shots, 2 * 64 )
codes = tf.reduce_mean(codes, axis=1, keep_dims=True) # K dimension
# Keep the shape (N, K, *)
codes = tf.tile(codes, [1, self.num_examples_per_class, 1])
return codes
def possibly_sample(self, distribution_params, stddev_offset=0.):
# input params distribution_params: ( ways, shots, ? )
means, unnormalized_stddev = tf.split(distribution_params, 2, axis=-1)
stddev = tf.exp(unnormalized_stddev)
stddev -= (1. - stddev_offset)
stddev = tf.maximum(stddev, 1e-10)
distribution = tfp.distributions.Normal(loc=means, scale=stddev)
if not self.is_meta_training:
return means, tf.constant(0., dtype=self._float_dtype)
samples = distribution.sample()
kl_divergence = self.kl_divergence(samples, distribution)
return samples, kl_divergence
def kl_divergence(self, samples, normal_distribution):
random_prior = tfp.distributions.Normal(
loc=tf.zeros_like(samples), scale=tf.ones_like(samples))
kl = tf.reduce_mean(
normal_distribution.log_prob(samples) - random_prior.log_prob(samples))
return kl
def predict(self, inputs, weights):
# param inputs: ( ways, shots, 640 ), weights: ( ways, shots, 640 )
after_dropout = tf.nn.dropout(inputs, rate=self.dropout_rate)
# This is 3-dimensional equivalent of a matrix product, where we sum over
# the last (embedding_dim) dimension. We get [N, K, N, K] tensor as output.
# ( ways, shots, ways, shots )
per_image_predictions = tf.einsum("ijk,lmk->ijlm", after_dropout, weights)
# Predictions have shape [N, K, N]: for each image ([N, K] of them), what
# is the probability of a given class (N)?
# ( ways, shot, ways )
predictions = tf.reduce_mean(per_image_predictions, axis=-1)
return predictions
def calculate_inner_loss(self, inputs, true_outputs, classifier_weights):
# inputs: ( ways, shots, 640 ), outputs: ( ways, shots, 1 ), classifier_weights: ( ways, shots, 640 )
model_outputs = self.predict(inputs, classifier_weights) # model_outputs: ( ways, shot, ways )
model_predictions = tf.argmax(
model_outputs, -1, output_type=self._int_dtype) # model_predictions: ( ways, shot )
accuracy = tf.contrib.metrics.accuracy(model_predictions,
tf.squeeze(true_outputs, axis=-1))
return self.loss_fn(model_outputs, true_outputs), accuracy # loss: ( ways, shots )
def save_problem_instance_stats(self, instance):
num_classes, num_examples_per_class, embedding_dim = instance.get_shape()
if hasattr(self, "num_classes"):
assert self.num_classes == num_classes, (
"Given different number of classes (N in N-way) in consecutive runs.")
if hasattr(self, "num_examples_per_class"):
assert self.num_examples_per_class == num_examples_per_class, (
"Given different number of examples (K in K-shot) in consecutive"
"runs.")
if hasattr(self, "embedding_dim"):
assert self.embedding_dim == embedding_dim, (
"Given different embedding dimension in consecutive runs.")
self.num_classes = num_classes
self.num_examples_per_class = num_examples_per_class
self.embedding_dim = embedding_dim
@property
def dropout_rate(self):
return self._dropout_rate if self.is_meta_training else 0.0
def loss_fn(self, model_outputs, original_classes):
# param model_outputs: ( ways, shots, ways ), original_classes: ( ways, shots, 1 )
# original_classes: ( ways, shots )
original_classes = tf.squeeze(original_classes, axis=-1)
# Tensorflow doesn't handle second order gradients of a sparse_softmax yet.
# one_hot_outputs: ( ways, shots, ways )
one_hot_outputs = tf.one_hot(original_classes, depth=self.num_classes)
return tf.nn.softmax_cross_entropy_with_logits_v2(
labels=one_hot_outputs, logits=model_outputs) # ( ways, shots )
def grads_and_vars(self, metatrain_loss):
"""Computes gradients of metatrain_loss, avoiding NaN.
Uses a fixed penalty of 1e-4 to enforce only the l2 regularization (and not
minimize the loss) when metatrain_loss or any of its gradients with respect
to trainable_vars are NaN. In practice, this approach pulls the variables
back into a feasible region of the space when the loss or its gradients are
not defined.
Args:
metatrain_loss: A tensor with the LEO meta-training loss.
Returns:
A tuple with:
metatrain_gradients: A list of gradient tensors.
metatrain_variables: A list of variables for this LEO model.
"""
metatrain_variables = self.trainable_variables
metatrain_gradients = tf.gradients(metatrain_loss, metatrain_variables)
nan_loss_or_grad = tf.logical_or(
tf.is_nan(metatrain_loss),
tf.reduce_any([tf.reduce_any(tf.is_nan(g))
for g in metatrain_gradients]))
regularization_penalty = (
1e-4 / self._l2_penalty_weight * self._l2_regularization)
zero_or_regularization_gradients = [
g if g is not None else tf.zeros_like(v)
for v, g in zip(tf.gradients(regularization_penalty,
metatrain_variables), metatrain_variables)]
metatrain_gradients = tf.cond(nan_loss_or_grad,
lambda: zero_or_regularization_gradients,
lambda: metatrain_gradients, strict=True)
return metatrain_gradients, metatrain_variables
@property
def _l2_regularization(self):
return tf.cast(
tf.reduce_sum(tf.get_collection(tf.GraphKeys.REGULARIZATION_LOSSES)),
dtype=self._float_dtype)
@property
def _decoder_orthogonality_reg(self):
return self._orthogonality_reg