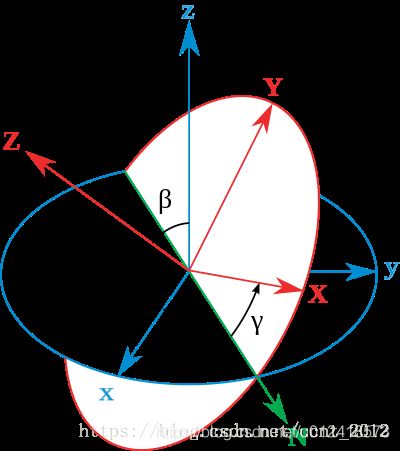
视觉SLAM十四讲--第三章旋转公式
第三讲 三维空间刚体运动
本讲的主要问题是:一个刚体在三维空间中的运动是如何描述的。(一次旋转加一次平移)
3.1 旋转矩阵
1…点和向量,坐标系
点–
向量—指具有大小(magnitude)和方向的量。可以想象成从原点指向某处的一个箭头。是空间中的一样东西。在没有确定坐标系的情况下,不能讨论向量的坐标。如果确定了坐标系,即一个线性空间的基( e 1 , e 2 , e 3 e_1,e_2,e_3 e1,e2,e3)
日了狗,没保存,丢了
增加个博客内容吧:https://zhuanlan.zhihu.com/p/78987582 (介绍了点积,叉积,旋转等内容,较详细)
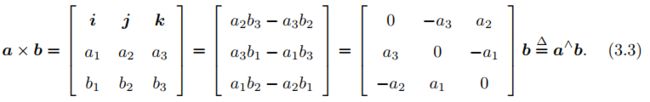

对等式左右同时左乘

中间矩阵为R,为两组基之间的内积,称为旋转矩阵。旋转矩阵是一个行列式为1的正交矩阵,反之,行列式为1的正交矩阵也是一个旋转矩阵。
旋转矩阵为正交阵,他的逆(即转置)描述了一个相反的旋转。
- 变换矩阵与齐次坐标
欧式空间描述旋转与平移,存在一个小问题,即多次变换,导致非线性
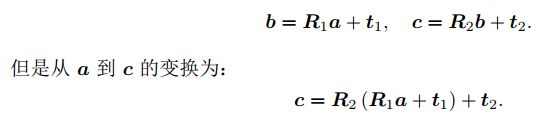
于是引入齐次坐标和变换矩阵重写:使得整个关系变成了线性关系, T T T称为变换矩阵。
3.3 旋转向量和欧拉角
1.旋转向量
旋转矩阵的缺点:
(1)九个量,只需三个自由度,造成冗余。而变换矩阵用十六个量表达六自由度的变换。
(2)自身带有约束:正交矩阵,且行列式为1。变换矩阵亦是如此,这些约束使得求解困难。
旋转向量:用一个旋转轴和一个旋转角来表示旋转。 刚体变换可以用六个自由度表示。采用方向与旋转轴一致,长度等于旋转角的三维旋转向量描述旋转,因此,变换矩阵就可以使用一个旋转向量和一个平移向量表达,维数为六维(就是李代数,下一章详细介绍,这里只是知道如何表达)。
旋转向量和旋转矩阵之间的转换:
假设旋转轴为k,角度为 θ \theta θ,对应的旋转向量 θ k \theta k θk。
补充:罗德里格斯公式:
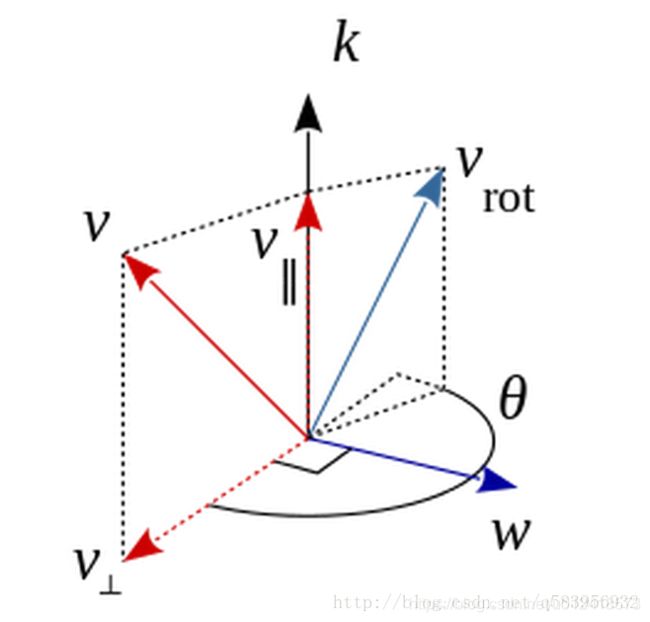
向量 v \bm{v} v在旋转轴 k \bm{k} k所在坐标系 k = [ v ∥ , v ⊥ , w ] \bm{k}=[v_\parallel,v_\perp, w] k=[v∥,v⊥,w]下可分解为两个方向的分量相加,即, v = v ∥ + v ⊥ \bm{v=v_\parallel+v_\perp} v=v∥+v⊥,绕旋转轴旋转 θ \theta θ角度后的向量为 v r o t \bm{v_{rot}} vrot.
其中 v ⊥ \bm{v_\perp} v⊥与 k \bm{k} k正交, v ∥ \bm{v_\parallel} v∥为 v \bm{v} v在 k \bm{k} k上的正交投影。由正交投影公式:
v ∥ = ( k . v ) k v_\parallel=\bm{(k.v)k} v∥=(k.v)k
根据上边的公式可以写成:
v ⊥ = v − v ∥ = v − ( k . v ) k \bm{v_\perp = v-v_\parallel = v-(k.v)k} v⊥=v−v∥=v−(k.v)k,而 v ∥ \bm{v_\parallel} v∥与 v \bm{v} v重合,旋转时不变。 w = k × v ⊥ = k × v \bm{w=k\times v_\perp=k\times v} w=k×v⊥=k×v
根据图中向量和角度之间的关系,可以得出结论:
v r o t = v ∥ − v ⊥ c o s ( π − θ ) + w s i n ( π − θ ) = v ∥ + v ⊥ c o s θ + w s i n θ \bm{v_{rot}=v_\parallel-v_\perp cos(π-\theta)+w sin(π-\theta)=v_\parallel+v_\perp cos\theta+w sin\theta} vrot=v∥−v⊥cos(π−θ)+wsin(π−θ)=v∥+v⊥cosθ+wsinθ
带入相关公式(向量交换律,叉乘,反对称等性质):
v r o t = v ∥ + v ⊥ c o s θ + w s i n θ \bm{v_{rot}=v_\parallel+v_\perp cos\theta+w sin\theta} vrot=v∥+v⊥cosθ+wsinθ
= ( k . v ) k + ( v − ( k . v ) k ) c o s θ + ( k × v ) s i n θ \bm{(k.v)k+ (v-(k.v)k) cos\theta+ (k\times v) sin\theta} (k.v)k+(v−(k.v)k)cosθ+(k×v)sinθ
= c o s θ v + ( 1 − c o s θ ) ( k . v ) k + ( k × v ) s i n θ \bm{=cos\theta v+(1-cos \theta ) (k.v)k+ (k\times v) sin\theta} =cosθv+(1−cosθ)(k.v)k+(k×v)sinθ
= ( c o s θ I + ( 1 − c o s θ ) k k T + s i n θ k ∧ ) v \bm{=(cos\theta I+(1-cos \theta ) kk^T+ sin\theta k\wedge)v } =(cosθI+(1−cosθ)kkT+sinθk∧)v
R = c o s θ I + ( 1 − c o s θ ) k k T + s i n θ k ∧ \bm{R=cos\theta I+(1-cos \theta ) kk^T+ sin\theta k\wedge} R=cosθI+(1−cosθ)kkT+sinθk∧
对矩阵 R \bm{R} R左右求秩,根据公式(3.3)得到:
t r ( R ) = c o s θ t r ( I ) + ( 1 − c o s θ ) t r ( k k T ) + s i n θ t r ( k ∧ ) = 3 c o s θ + ( 1 − c o s θ ) = 1 + 2 c o s θ \bm{tr(R)=cos\theta tr(I)+(1-cos \theta ) tr(kk^T)+ sin\theta tr(k\wedge)= 3cos\theta+(1-cos\theta) =1+2cos\theta} tr(R)=cosθtr(I)+(1−cosθ)tr(kkT)+sinθtr(k∧)=3cosθ+(1−cosθ)=1+2cosθ
可以得出: θ = a r c c o s ( ( t r ( R ) − 1 ) / 2 ) \theta=arccos((tr(\bm{R})-1)/2) θ=arccos((tr(R)−1)/2)
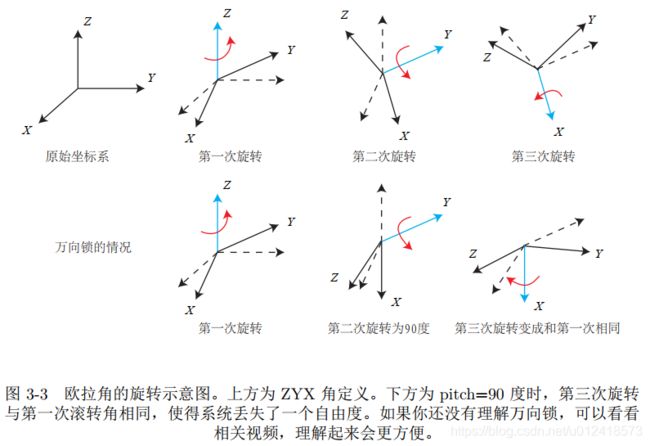
2.欧拉角
万向锁问题
3.4 四元数
补充知识:
复数表示旋转的描述 :https://editor.csdn.net/md/?articleId=107150734
3D旋转和罗德里格斯公式:https://editor.csdn.net/md/?articleId=107173576
四元数定义
旋转矩阵用九个量描述三自由度的旋转,具有冗余性;欧拉角和旋转向量是紧凑的,但
具有奇异性。
四元数
是 Hamilton 找到的一种扩展的复数. 它既是紧凑的,也没有奇异性。如果说缺点的话,四
元数不够直观,其运算稍为复杂一些。
3.2 四元数与3D旋转
将一个向量 v \bm{v} v沿着一个用单位向量所定义的旋转轴 u \bm{u} u旋转 θ \theta θ度,因此,可以 v \bm{v} v拆分成正交于旋转轴向量 v ⊥ \bm{v_\perp} v⊥和平行于旋转轴的向量 v ∥ \bm{v_\parallel} v∥,即 v = v ⊥ + v ∥ \bm{v=v_\perp+v_\parallel} v=v⊥+v∥








结论:如果绕着同一个轴 u \bm{u} u连续旋转 θ \theta θ度两次,等同意直接绕轴 u \bm{u} u旋转2 θ \theta θ度.