c#树型分类结构统计表格的通用实现方式
在开发过程中,经常会遇到树型的分类结构,而项目后期会根据分类对数据进行统计,不管是后台拼接table还是前后台分离开发方式,总是不能避免对树型结构的表头创建及同项单元格的合并问题,而后面的计算统计列也可能因为分类层级的参差不齐而需要加许多冗长复杂的条件判断,不论是逻辑阅读与后期代码维护的复杂性,复用性都是非常糟糕可怕的,所以想了一个相对通用的解决方式来简化统计列表的实现,使得复用性增强,逻辑代码清楚,下面来讲解一下思路。
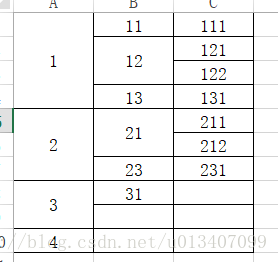
首先,来看一个一般性的统计列表A,这是我在excel中简单合并的一个类似于统计列表形式的单元格,可能大家认为这种代码实现
列表A 列表B
起来很简单,几层循环就解决了,但是如果是4层,5层这种层级逻辑,那代码的复杂程度是不是要成倍的增长了,所以我们需要一个相对通用一般性的解决方案,使得问题的解决方式有可扩展性与移植性。
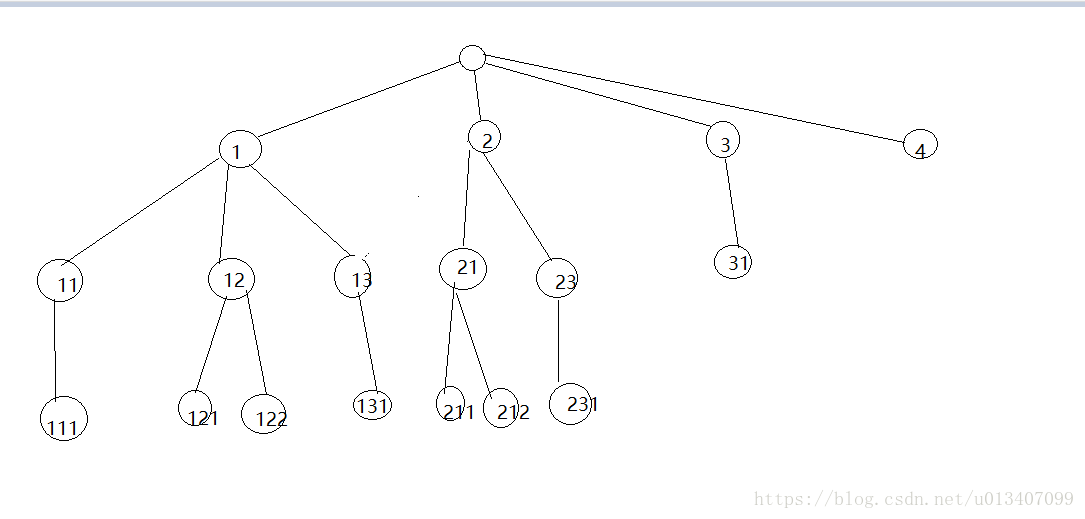
我的思路是先实现合并前数据,也就是全是单元格的形式,如图列表B,可能这样的列表不太清楚,那我们再拆分成树,更为直观,也有利于后续的思路展开,如树A
树A
可能画的有点丑,大家见谅,然后我们依次从左到右拆分一下树的路径,
1-11-111
1-12-121
1-12-122
1-13-131
2-21-211
2-21-212
相信到这里大家已经可以发现,这里的树的路径就是table中对应的行,路径中的节点对应的就是table中的列,我们只要把分类数据填充到树中,然后把树的每条路径按顺序抽出来,那不管多么复杂的层级关系,都是简单的行与列的两层循环就可以构建出来了,但是还要考虑到一个问题就是,列表的列是要相等的,那对于不同深度的每条路径,我们就需要补上空节点,直到底层的叶子节点的深度为树的最大深度就可以了,想到就先做起来,不足之处可以在编写中完善。
先看下树结构包含的一些信息
public HPTreeNode TopNode { set; get; }
public int MaxDeep { set; get; }
public int EachLevelCodeLenth { set; get; }
public DataView TreeData { set; get; }
public DataView TreeDataCopy { set; get; }
public string ItemText { set; get; }
public string ItemValue { set; get; }
public string TopNodeCode { set; get; }
public string TopNodeName { set; get; }
private List NoChildNodeList { set; get; }
其中MaxDeep是树的最大深度,用于判断补齐空节点的,EachLevelCodeLenghth树的Code模式下的每级代码的长度如0001一级节点的长度就为4,ItemTex与ItemValue是传入从数据库获取的层级数据的代码与名称FieldName
再看下节点的数据结构
public string NodeCode { set; get; }
public string NodeName { set; get; }
public int NodeDeep { set; get; }
public HPTreeNode ParentNode { set; get; }
public List ChildNodeList { set; get; }
public bool IsHaveChild { set; get; }
public bool IsEmptyNode { set; get; }
public int AllSubChildNum { set; get; } 包含常规的节点名称,节点的值,节点所在树的深度,节点的父级节点引用,子节点数组,是否有孩子节点,是否是空节点,节点下所包含的所有节点数,第一步我们先把把数据填充到树型结构中,在树的初始化中先构建顶级节点,然后通过递归调用的方式填充
TopNode = new HPTreeNode();
TopNode.NodeCode = TopNodeCode;
TopNode.NodeName = TopNodeName;
TopNode.IsEmptyNode = false;
TopNode.IsHaveChild = true;
TopNode.ParentNode = null;
TopNode.NodeDeep = 1;
int maxdeep = 1;
//节点下所有底层节点数目
int allnochildsubnum = 1;
List ChildNodeList = null;
InsertTreeInfo(TopNode, TreeData, out ChildNodeList, ref maxdeep);
TopNode.ChildNodeList = ChildNodeList;
this.MaxDeep = maxdeep; public void InsertTreeInfo(HPTreeNode ParentNode, DataView TreeData, out List ChildNodeList, ref int MaxDeep)
{
ChildNodeList = new List();
DataTable CopyDataTable = TreeData.Table.Copy();
CopyDataTable.Clear();
for (int i = 0; i < TreeData.Count; i++)
{
CopyDataTable.ImportRow(TreeData[i].Row);
}
DataView CopyDataView = CopyDataTable.DefaultView;
AllChildNodeList.Add(ParentNode);
CopyDataView.RowFilter = string.Format(" Len({0})={1} and {0} like '{2}%'", ItemValue, ParentNode.NodeCode.Length + EachLevelCodeLenth, ParentNode.NodeCode);
for (int i = 0; i < CopyDataView.Count; i++)
{
string nodecode = Convert.ToString(CopyDataView[i][ItemValue]);
string nodename = Convert.ToString(CopyDataView[i][ItemText]);
HPTreeNode node = new HPTreeNode();
node.NodeCode = nodecode;
node.NodeName = nodename;
node.ParentNode = ParentNode;
node.IsEmptyNode = false;
node.IsHaveChild = IsHaveChild(nodecode, TreeData);
node.NodeDeep = ParentNode.NodeDeep + 1;
if (MaxDeep < ParentNode.NodeDeep + 1)
{
MaxDeep = ParentNode.NodeDeep + 1;
}
List nextnodelist = null;
if (node.IsHaveChild)
{
InsertTreeInfo(node, TreeData, out nextnodelist, ref MaxDeep);
}
node.ChildNodeList = nextnodelist;
ChildNodeList.Add(node);
if (!node.IsHaveChild)
{
NoChildNodeList.Add(node);
}
AllChildNodeList.Add(node);
}
} public void FillTree()
{
foreach (HPTreeNode node in NoChildNodeList)
{
FillEmptyTreeNode(node);
}
} ///
/// 根据树的某一结点情况添加空节点,使得树的每条路线都得以达到最大深度,且最底层至少有一个节点(包含空节点)
///
public void FillEmptyTreeNode(HPTreeNode ParentNode)
{
List list = ParentNode.ChildNodeList;
//如果孩子节点不存在且当前节点深度未达到最大深度,添加空节点
if (null==list)
{
if (ParentNode.NodeDeep!=this.MaxDeep)
{
HPTreeNode emptynode = new HPTreeNode();
emptynode.NodeCode = "";
emptynode.NodeName = "";
emptynode.IsEmptyNode = true;
emptynode.ParentNode = ParentNode;
emptynode.NodeDeep = ParentNode.NodeDeep + 1;
//如果下级还未达到最大,则此节点有孩子节点
if (ParentNode.NodeDeep + 1 != this.MaxDeep)
{
emptynode.IsHaveChild = true;
}
else
{
emptynode.IsHaveChild = false;
}
list = new List();
list.Add(emptynode);
ParentNode.ChildNodeList = list;
//如果没有孩子节点则到最底层,加入到底层的数组
if (!emptynode.IsHaveChild)
{
NoChildNodeContainsEmptyList.Add(emptynode);
}
else
{
//有孩子节点继续往下加
FillEmptyTreeNode(emptynode);
}
}
else
{
NoChildNodeContainsEmptyList.Add(ParentNode);
}
}
} 填充完毕后我们就可以开始将路径抽出,路径自上往下可能找起来比较复杂,那么我们从底层节点向上寻找路径,这样就会变的非常简单了,先添加一个table统计表的对象,然后往里面构造
public class TreeTableLine
{
public string LineCode { set; get; }
public List LineList { set; get; }
} public List ConverTreeToLine()
{
FillTree();
List list = new List();
foreach (HPTreeNode node in NoChildNodeContainsEmptyList)
{
string linecode = GetLastNoEmptyParentNodeCode(node);
List linelist = new List();
GetLineNodeList(node, ref linelist);
TreeTableLine treetableline = new TreeTableLine();
treetableline.LineCode = linecode;
treetableline.LineList = linelist;
list.Add(treetableline);
}
return list;
} 这样我们就能使用两层循环开始构造了,但是我们还要考虑到合并的操作,所以要记录每个节点下最多的子节点树,因为统计表是已最小级别的数目来计算行数的,合并时,保持节点数为1的不合并(节点本身也算在数量内),其余的第一次合并,遇到相同的不合并,使用数组记录既可以,不要费脑子的去算下标关系,实在是太麻烦了,还有一点要注意的是,后续列的计算可能由于类别的层级不同,例如三级类别没有要追溯到二级甚至一级,需要判断很多情况,我们给行规定一个最小级别的Code为行标识,用于计算对应的数据,会变的非常方便
//把种类属性结构初始化到树的结构体中
HPTree hptree = new HPTree(type, "", "", "ClassName", "ClassCode", 4);
DataView InOrder = KM.GetProjectMaterialIn(Request.QueryString["ProjectID_JSGC"]);
DataView OutOrder = KM.GetProjectMaterialOut(Request.QueryString["ProjectID_JSGC"]);
DataView BackOrder = KM.GetMaterialBack(Request.QueryString["ProjectID_JSGC"]);
int max = KM.GetMaxMaterialTypeCount(Request.QueryString["ProjectID_JSGC"]);
string tablecontent = string.Empty;
List tablelist = null;
//将树形结构补齐,达到每个底层还在节点都一样,就可以将树型结构的路径依次抽出作为表的行
if (!IsShowNoZero)
{
tablelist = hptree.ConverTreeToLine();
}
else
{
tablelist = KM.ConverTreeToLineWithOutNoOperateData(hptree, InOrder, OutOrder, BackOrder);
}
List rowspanlist = new List();
tablecontent += "";
#region 表头
//根据种类深度获取表头
List dynamichead = new List();
dynamichead.Add("材料类别");
dynamichead.Add("子类1级");
dynamichead.Add("子类二级");
tablecontent += "";
for (int i = 0; i < max; i++)
{
tablecontent += string.Format("{0} ", dynamichead[i]);
}
tablecontent += " ";
#endregion
//行
for (int i = 0; i < tablelist.Count; i++)
{
tablecontent += "";
//列
List rowlist = tablelist[i].LineList;
//去除树路径的顶级节点
rowlist.RemoveAt(rowlist.Count - 1);
//倒叙,因为路径是由下往上找到的
//拼接种类表头,包括合并
for (int j = rowlist.Count - 1; j >= 0; j--)
{
int nochildsubnodecount = 0;
hptree.GetNoChildNodeCount(rowlist[j], ref nochildsubnodecount);
if (nochildsubnodecount == 1)
{
tablecontent += string.Format("{0} ", rowlist[j].NodeName, nochildsubnodecount);
}
else
{
if (!rowspanlist.Contains(rowlist[j].NodeCode))
{
tablecontent += string.Format("{0} ", rowlist[j].NodeName, nochildsubnodecount);
rowspanlist.Add(rowlist[j].NodeCode);
}
}
}
//加入种类后的数据拼接
string linecode = tablelist[i].LineCode;
//是否有操作信息,即入库信息
bool ishaveoperatedata = true;
double kuncunnum = KM.GetKuCunNum(InOrder, OutOrder,BackOrder, linecode, out ishaveoperatedata);
string unit = string.Empty;
map.TryGetValue(linecode, out unit);
//单位
tablecontent += string.Format("{0} ", unit);
//数量
if (ishaveoperatedata)
{
tablecontent += string.Format("{1} ", linecode, kuncunnum.ToString("0.00"));
}
else
{
tablecontent += " ";
}
tablecontent += "
";
BodyControls.InnerHtml = tablecontent;
} 这样就构造出我们想要的一般性解决方案了,可能还存在很多不足的地方,欢迎大家提出来
源码附上:https://download.csdn.net/download/u013407099/10428339