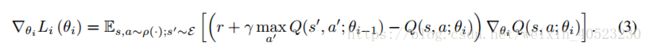【论文翻译】Playing Atari with Deep Reinforcement Learning

摘要：我们第一个提出了"利用强化学习从高维输入中直接学习控制策略"的深度学习模型。该模型是一个卷积神经网络，经过Q-learning训练，输入为原始像素，输出为：“用来估计未来reward”的值函数。我们将我们的方法应用于游戏环境下的7款atari 2600游戏，没有调整过架构或学习算法。我们发现它在6个游戏中超越了所有以前的方法，并且在3个游戏中超过了人类专家。

---

• 1 . Introduction

  • 直接从视觉和语言等高维感官输入中学习如何控制agent是强化学习（RL）的长期挑战之一。大多数成功的RL应用程序，都依赖基于人工特征的策略或者值函数。显然，这些系统的性能在很大程度上依赖于特征的质量。
  • 最近，深度学习的发展使人们有机会从原始感官数据中提取高层特征，这使得计算机视觉和语音识别产生了突破。这些方法运用了一系列的神经网络架构，包括复杂网络，多层感知器，有限波兹曼机器和循环神经网络，同时利用了监督和无监督的学习。似乎很自然地会问：类似的技术是否也能对RL和感官数据有帮助呢？
  • 从深度学习的角度，我们对强化学习提出了几个疑问。
    • 第一：迄今为止，大多数成功的深度学习应用程序都需要大量的手工标记训练数据。
    • 第二：RL算法必须能够从频繁稀疏、噪声和延迟的标量奖励信号中学习。监督学习中：输入与目标之间是直接联系的。因此，action与reward之间的延迟(可能长达数千步)是个棘手的问题。
    • 第三：大多数深度学习算法假设数据样本是独立的，而在强化学习中，通常会遇到高度相关的序列。
    • 第四：在RL中，随着算法不断学习新的action，“agent根据action探索得到的数据”的分布也会发生变化。这对于“假设一个固定的底层分布”的深度学习来说是有问题的。
  • 这篇论文证明了：一个复杂的神经网络可以通过RL克服这些挑战，从“复杂环境的原始视频数据”中学习到成功的控制策略。该网络采用Q-learning算法的一种变体进行训练，采用随机梯度下降法更新权值。为了缓解数据相关性问题和非平稳分布的问题，我们使用了一个经验重放机制，它随机地对以前的transition（从一个状态切换到另一个状态）进行采样，从而使训练分布与过去的许多行为保持一致。
  • 我们将此方法应用于在街机环境中的Atari 2600游戏。Atari2600是一个具有挑战性的RL试验环境，具有高维视觉输入(210×160 RGB视频60 hz)和一组不同的有趣的任务的智能体，对人类玩家是很难的。我们的目标是创建一个单一的神经网络agent，能够成功地学习尽可能多的游戏。该神经网络没有提供任何特定游戏的信息或人工设计的视觉特征，不知道游戏模拟器的内部状态；它只从视频输入、奖励和终端信号以及可能的动作中学习——就像人类一样。此外，网络架构和所有用于训练的超参数在整个游戏中保持不变。到目前为止，在我们尝试过的七款游戏中，有六款游戏的RL算法都表现得很出色，其中三款游戏的RL算法都超过了专家水平。

• 2 . Background

  • 我们考虑“agent与环境  交互”这一任务(在本例中是Atari模拟器)，这些任务包含一系列的动作actions、状态observations和奖励rewards。在每个时间步中，agent从合法的动作集合A ={1，…K }中选择一个动作at。动作at被发送给模拟器并返回游戏的状态和游戏的分数。一般来说  是随机的。agent看不见游戏模拟器的内部状态；但是，agent所观察到的图像 xt∈Rd 来自游戏模拟器，它是一个向量（表示当前屏幕的原始像素值）。此外，它还会收到一个“表示游戏分数变化”的奖励rt。注意，一般来说，游戏分数可能取决于整个先前的动作和状态序列；关于一个动作的反馈可能要经过数千步的时间才会收到。
  • 由于agent只观察当前屏幕的图像，整个“与环境交互的任务”是仅能够被部分观察到的。仅从当前屏幕xt中完全理解当前的情况是不可能的。因此我们研究“动作和状态”的序列：st = x1, a1, x2，a2，… xt  ,基于这些序列进行策略的学习。假设游戏模拟器中的所有序列都在有限的时间步长内结束。这种形式产生了一个大而有限的马尔可夫决策过程(MDP)，其中每个状态是一个不同的状态。因此，我们可以对MDP使用标准的强化学习方法。
  • agent的目的是：通过选择action，来最大化未来的回报rewards。我们做了标准假设：未来奖励的折扣因子为

    γ，并且定义t时刻打过折的回报是，其中T是游戏结束时的步长。

  • 我们将最优的动作价值函数 action-value function 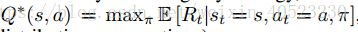     定义为：“在看到一些序列s,然后采取一些动作a”后，获得的最大收益。其中，π是一个策略，用来将序列映射到动作。

  • 最优的动作价值函数遵循一个重要的特征，即Bellman方程。

  • 这是基于以下直觉：如果已知所有可能动作a‘的最优值Q∗(s′,a′)，那么最优策略就是选择出这样一个a'，能够使得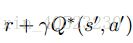的期望值最大。即，下式：

  • 

  • 许多强化学习算法背后的基本思想是：通过使用Bellman方程作为迭代更新，来估计action-value函数的值，                             Qi+1(s; a) =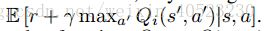。这种值迭代算法收敛于最优actionvalue函数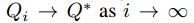。但是在实践中，这种基本方法是完全不切实际的，因为每个序列的action-value函数都是单独估计的，没有任何一般化。取而代之，通常使用“函数逼近器”来估计action-value函数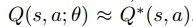，。在强化学习中，这通常是一个线性函数逼近器，但有时也会使用非线性函数逼近器，如神经网络。我们将权值为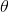的神经网络函数逼近器称为Q-network。Q-Network可以在每一轮迭代i，通过“最小化损失函数Li(θi)的序列”来进行训练。

  • 

  • 其中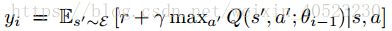，是第i轮迭代的目标target（也就是真实值）。ρ(s，a)是在序列s和动作a上的概率分布，我们称之为“行为分布”。当优化损失函数Li (θi)时，上一轮迭代的参数θi-1当做已知固定值，同时执行s处的a后，r也是已知的，计算出yi，把这个yi当做target。   注意，目标target依赖于网络权值；这与监督学习的目标不同，监督学习的目标target在学习开始之前是固定的。对损失函数求关于权值的微分得到如下梯度

  • 

  • 相比于在上面的梯度中计算全部的期望，采用随机梯度下降法对损失函数进行优化是一种方便的计算方法。如果权重在每一个时间步骤之后更新，并且期望被来自行为分布和游戏模拟器的单个样本所取代，那么我们就会得到熟悉的q-learning算法。

  • 注意，这个算法是无模型的：它直接使用 游戏模拟器 中的样本来解决强化学习任务，没有明确构造的估计值。这也是一种off-policy：它学习了贪婪策略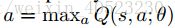，遵循一个“确保对状态空间的充分探索”的行为分布。实际中，行为分部通常根据“ 贪婪策略”来选择：1-的概率选择贪婪策略，的概率选择随机策略。

• 3 . Related Work

  • 强化学习最著名的案例是TD-gammon，这是一个完全通过强化学习和自我游戏来学习的游戏程序，它达到了一个超人级别的水平。TD-gammon使用了一种类似Q-learning的无模型强化学习算法，并使用一个带有一个隐藏层的多层感知器来逼近value函数。

  • 然而，早期TD-gammon的尝试：将同样的方法应用到国际象棋、围棋和西洋跳棋上都不太成功。这导致人们普遍认为TD-gammon方法是一种只适用于西洋双陆棋的特殊情况，可能是因为骰子滚动的随机性有助于探索状态空间，并使value函数特别平滑。

  • 此外，结合无模型强化学习算法，例如具有非线性函数逼近器的q-learning或者indeed with off-policy learning可以导致Q-network发散。随后，强化学习的大部分工作都集中在“具有更好的收敛性保证的线性函数逼近器”上。最近，人们又开始研究将深度学习与强化学习相结合。深度神经网络被用于评估环境  ；利用有限玻尔兹曼机对value函数或者策略进行估计;此外，用梯度时间差分方法部分解决了Q-learning中的发散问题。当用非线性函数近似器对策略进行评估时，这些方法被证明是收敛的。

  • 也许以前与我们的方法最相似的工作是神经拟合Q-learning (NFQ)。但是，它使用的批更新具有“每次迭代的计算成本都与数据集的大小成正比”这一特点，而我们考虑的是随机梯度，每次迭代成本低且可扩展到大型数据集的更新。NFQ还成功地应用于简单的实际控制任务，使用纯视觉输入，首先使用深度自动编码器来学习任务的低维度表示，然后将NFQ应用到这个低纬度表示中。相比之下，我们的方法直接从视觉输入端应用强化学习;因此它可能会学到与action-value有直接关系的特性。Q-learning此前也曾与经验重放和简单的神经网络结合在一起，但从低维度状态开始，而不是原始的视觉输入。

  • [3]介绍了Atari 2600仿真器作为增强学习平台的使用，使用了线性函数逼近和通用视觉特征的标准增强学习算法。随后，通过使用更多的特征，结果得到了改善，并使用拔河哈希将特征随机投射到低维空间[2]中。当使用模拟器的复位工具反复地对确定性序列进行训练时，这些策略能够利用一些Atari游戏中的设计缺陷。

• 4 . Deep Reinforcement Learning

  • 最近计算机视觉和语音识别方面的突破依赖于在非常大的训练集上有效地训练深层神经网络。最成功的方法是直接从原始输入进行训练，使用基于随机梯度下降的轻量级更新。通过向深层神经网络输入足够的数据，通常可以学习到人工特征更好的表示。这些成功激发了我们强化学习的方法。我们的目标是将增强学习算法与直接对RGB图像进行操作的深度神经网络结合起来，利用随机梯度更新有效地处理训练数据。
  • Tesauros的 TD-Gammon架构为这种方法提供了一个起点。这个架构更新网络的参数，这个网络从“算法与环境的交互中”提取估算了value-function。由于这种方法在20年前就能超过最好的人类西洋双陆棋选手，我们很自然地想知道二十年的硬件改进，加上现代深度神经网络架构和可扩展的RL算法是否会取得重大进展。
  • 与TD-Gammon和类似的在线方法形成对比，我们使用一种被称为经验重放的技术，我们在每一个时间步长中存储agent的经验，把每一步的经验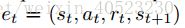存储在数据集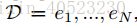中。在算法的内部循环中，我们从存储的样本池中随机抽取e ∼ D，并用Q-learning更新或小批量更新。在执行 经验重放 后，agent根据 贪婪策略 选择并执行一个action。由于使用任意长度的历史作为神经网络的输入可能很困难，取而代之，我们的q函数作用于固定长度的表示，这个表示是由 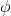函数 提供的。算法1给出了完整算法，我们称之为深度Q-learning。
  • 
  • 这种方法比标准的在线Q-learning[23]有几个优点。
    • 首先，经验的每一步都有可能用于许多权重更新，从而提高数据效率。
    • 第二，直接从连续的样本中学习效率很低，因为样本之间的相关性很强；随机化样本打破了这些相关性，因此减少了更新的方差。
    • 第三，当在策略上学习时，当前参数决定了下一个参数所训练的数据样本。例如，如果函数值最大的动作是左移，则训练样本将由来自左手侧的样本主导；如果最大化的动作切换到右边，那么训练的分布也会改变。因此，可能出现不希望有的反馈回路，且这些参数可能会陷入一种较差的局部最小值，或者甚至是灾难性的。通过使用经验重放，行为分布在它以前的许多状态上是平滑的，避免参数的振荡或发散。
  • 这种方法是有局限性的，因为内存不区分经验的重要程度，并且由于内存大小N有限，总是会用最近的经验覆盖以前的经验。并且，此方法中，均匀采样对回放内存中的所有经验都相同对待。一种更复杂的抽样策略可能会强调：“我们应该对能学到最多的步骤进行采样”，类似于优先处理的排序。

  • 4.1   Preprocessing and Model Architecture

    • 原始的Atari框架（210*160像素，128个颜色）对计算要求太高，因此，我们应用了一个预处理步骤来降低输入的维数。原始帧被预处理，首先将它们的RGB转换成灰度，并将其降采样到110*84的图像。最后的输入：裁剪成一个84*84的图像区域，这个区域大致可以捕捉到游戏区域。最后的裁剪阶段是必需的，因为我们使用的是2D卷积的GPU实现，它期望的是方形输入。对于本文的实验，算法1的函数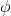将此预处理应用于历史的最后4帧，并将它们堆叠起来生成q函数的输入。
    • 存在几种“用神经网络将Q进行参数化”的方式。由于Q将历史-动作对映射到它们的Q值，历史和动作在以前一些方法已经被用作神经网络的输入。这种架构的主要缺点是：需要单独的前向传递来计算每个操作的q值，这导致计算成本与操作的数量成线性关系。输出对应于输入状态下单个动作的预测值。这种架构的主要优点是：只通过一个前向网络，能够计算给定状态下所有可能动作的q值。我们现在描述了所有7款雅达利游戏的架构。神经网络的输入是一个84*84*4的图像。第一个隐藏层：16个8 × 8 filters with stride 4 ，并进行非线性处理。第二个隐藏层：卷积了32个4 × 4 filters with stride 2，并进行非线性处理。最后的隐藏层是全连接的，由256个整流单元组成。输出层是一个全连接的线性层，对于每个有效动作只有一个输出。在我们考虑的游戏中，有效动作的数量在4到18之间变化。我们将使用我们的方法训练的卷积网络称为深度q网络(Deep Q-Networks, DQN)。

• 5   Experiments

  • 到目前为止，我们已经在七款流行的雅达利游戏上做了实验——梁骑士，突破，耐力，乒乓，Q*bert，海景，太空入侵者。我们在所有7款游戏中使用了相同的网络架构、学习算法和超参数设置，这表明我们的方法足够健壮，可以在各种游戏中工作，而不需要包含特定游戏的信息。当我们在真实的和未经修改的游戏中评估我们的智能体时，我们只在训练中对游戏的奖励结构做了一个改变。由于分数的大小在不同游戏有很大的不同，我们把所有的正回报都固定为1，所有的负回报都是1，而0奖励不变。以这种减少奖励的方式，限制了误差的导数规模，使算法在多个游戏中更容易使用相同的学习速率。同时，它会影响我们智能体的性能，因为它不能区分不同大小的奖励。
  • 在这些实验中，我们使用了RMSProp算法。mini-batch大小为32。在训练过程中，行为策略是贪婪的，从1到0.1线性退火，在第一百万帧中，此后固定为0.1.我们总共训练了1000万帧，并使用了100万张最新帧的重放记忆。
  • 按照以前的方法来玩Atari游戏，我们也使用了一个简单的帧跳过技术。更准确的说，智能体每k帧选择一次，它的最后一个动作在跳过的帧上重复。由于在一个步骤上运行模拟器需要比让智能体选择一个动作要少得多的计算，这种技术允许智能体在不显著增加运行时的情况下，玩大约k次的游戏。我们在所有游戏中都使用k = 4，除了《太空入侵者》，我们注意到使用k = 4会使激光看不见，我们用k = 3使激光可见，这个变化是所有游戏中超参数值的唯一区别。

  • 5.1  Training and Stability

    • 在监督学习中，通过在训练和验证集上评估模型，可以很容易地跟踪模型的性能。然而，在强化学习中，准确地评估一个agent在训练过程中的进展是具有挑战性的。由于我们的评估指标，是智能体在一集或一场游戏中平均收集的总报酬，我们会在训练期间周期性地计算它。平均总回报指标往往非常嘈杂，因为策略权重的微小变化会导致策略访问的状态的分布发生很大变化。图2中最左边的两个图显示了在训练中获得的平均总奖励是如何演变的。这两个平均的奖励图确实相当嘈杂，给人的印象是学习算法没有取得稳定的进展。另一个更稳定的度量标准是策略的动作价值估计函数Q，该函数表示：智能体从任何给定状态执行其策略所能获得的折扣奖励的估计。我们通过在训练开始前运行随机策略来收集一组固定的状态，并跟踪这些状态的最大预测Q的平均值。图2中最右边的两个图显示，最大预测Q的平均值的增长要比智能体获得的平均总回报平稳得多，并且在其他5个游戏中绘制相同的指标也会产生同样平滑的曲线。除了在训练中，对预测Q进行相对平稳的改进之外，我们在任何实验中都没有经历过发散问题。这表明，尽管缺乏理论上的收敛性保证，我们的方法能够以一种稳定的方式，利用强化学习信号和随机梯度下降来训练大型神经网络。

  • 5.2   Visualizing the Value Function

    • 图3显示了游戏Seaquest上的学习到的价值函数的可视化。图中显示，当敌人出现在屏幕左边(点A)时，预测值会发生跳跃。然后，该代理人向敌人发射一枚鱼雷，当鱼雷即将击中敌人时，预计的价值达到峰值（B点）。最后，在敌人消失后(点C)，该值大致下降到原来的值。图3展示了我们的方法能够了解价值函数如何在相当复杂的事件序列中演进。

  • 5.3    Main Evaluation

    • 
    • 我们将我们的结果与RL文献中的最佳表现方法进行了比较。Sarsa算法学习针对Atari任务人工设计的几个不同特征集的线性策略，并且我们展示性能最好的特性集的得分。Contingency算法应用了与Sarsa相同的基本方法，但通过对在智能体控制下的屏幕部分的学习表示来增强功能集。注意，这两种方法都包含了关于视觉问题的重要先验知识，使用背景减法并将128种颜色作为单独的通道。由于许多Atari游戏为每种类型的对象使用一种不同的颜色，所以将每种颜色作为一个单独的通道来处理，就类似于产生一个单独的二进制编码来映射每种对象类型的存在。不同之处在于，我们的智能体只接收原始的RGB屏幕截图作为输入，所以并且必须学会自己检测对象。
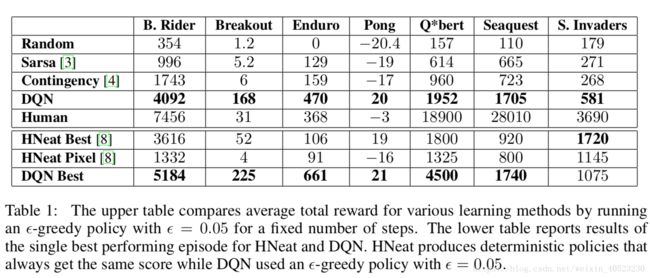
    • 作为智能体的补充，我们还展示了一名专业的人类游戏玩家，以及一项随机选择行动的策略的得分。人类的表现是在玩了大约两个小时的游戏后所获得的平均回报。请注意，我们展示的人类得分比Bellemare等展示的人类得分高得多。对于学习的方法，我们遵循Bellemare等人使用的评估策略并且展示在固定数量的步骤中运行 ε=0.05的 ε贪婪策略所获得的平均分数。表1的前5行显示了所有游戏的平均得分。我们的方法(DQN)在所有七款游戏中都比其他的学习方法有很大的优势，并且它几乎没有包含关于输入的先验知识。
    • 我们还将在表1的最后三行中对演进策略搜索方法进行比较。我们报告了这种方法的两组结果。HNeat Best反映了使用人工设计的对象检测算法获得的结果，该算法输出Atari屏幕上对象的位置和类型。HNeat Pixel 是通过Atari模拟器的特殊8色通道表示得到的，8色通道表示每个通道的对象标签映射。这个方法很大程度上依赖于找到一个具有决定性作用的状态序列。以这种方式学习的策略不大可能推广到随机扰动;因此，该算法仅对得分最高的单集进行评估。与此相反，我们的算法是在贪婪控制序列上进行评估的，因此必须在各种可能的情况下进行泛化。然而，我们表明除了空间入侵者以外的所有游戏，我们的最大结果(第8行)和平均结果(第4行)都获得了更好的性能。
    • 最后，我们证明了我们的方法在突破、耐力和乒乓方面取得了比专家级的人类棋手更好的表现，并且在横梁上接近人类的表现。《Q*bert》、《Seaquest》、《Space Invaders》等游戏，我们在这款游戏上远远比不上人类的表现，它们之所以更加有趣，是因为它们需要网络来找到一种长期扩展的策略。

• 6 . Conclusion

  • 这篇论文介绍了一种新的用于强化学习的深度学习模型，并展示了它对雅达利2600计算机游戏学习复杂控制策略的能力，只使用原始像素作为输入。我们还提出了一种在线Q-learning的变体，它将随机的minibatch与记忆回放相结合，以方便RL的深层网络训练。我们的方法在测试的7个游戏中有6个得到了最优秀的结果，并且没有对网络架构或超参数进行调整。