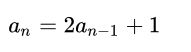※ 汉诺塔 数学意义上的详解 -(递归练习)
-------------------------------------------------2019.4.16日更新
有实验室后辈(学弟)说我之前写的这东西台阶太高了、不够螺旋梯度上升 表示根本听不懂
、然后我还被嘲讽了
...
我尼玛 、我会讲不清楚?
我再给你改一篇、绝对让你听懂、保证给你螺旋梯度、、
我他娘让你螺旋升天 、、(误)
------------------------------------------------------------------
首先,这篇文章中汉诺塔的实现用的是分治递归方法。 对于递归没有基础或者基础薄弱的同学建议先看看这篇文章:https://blog.csdn.net/weixin_41298915/article/details/89315587
然后回到汉诺塔:
“大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。” (百度百科)
换成数学的说明方法:
有三根杆子A,B,C。A杆上有 N 个 (N>1) 穿孔圆盘,盘的尺寸由下到上依次变小。要求按下列规则将所有圆盘移至 C 杆:
- 每次只能移动一个圆盘;
- 大盘不能叠在小盘上面。
(提示:可将圆盘临时置于 B 杆,也可将从 A 杆移出的圆盘重新移回 A 杆,但都必须遵循上述两条规则。)
问:如何移?最少要移动多少次?
在思考用编程语言实现之前我们先来讲讲它的数学解法,(动脑子)好多人都卡在这一步
我惯常默认你们能想的到三个盘子的排法:(不会的见下图)
(图片来自维基百科)
但我发现实际上大多数人其实对它这种排法的来源并不清楚;
所以这次讲解就从最简单的两个盘子的排列讲起,
两个的话,只需要先把小的放到中间(B)、大的放到右面(C),然后再把小的放到大的(C)上面;
只要你能认真读完汉诺塔规则那便肯定能把这一步走出来。
我们不妨把中间的位置叫做缓冲区(B)、右面的位置(C)叫做目标区域,
那上面的过程就可以写成:把小盘放到缓冲区、把大盘放到目标区、再把小的放到目标区。
而刚刚讲的这一个最简单的步骤就是汉诺塔问题的核心;
现在我们来看看三阶的汉诺塔
如上图,它的执行顺序是 先把小的放到C上、再中到B上、再小到中上、再大到C上、再小到A上、再中到大上、再小到中上;
怎么样,是不是觉得很眼熟?
没错,事实上三阶汉诺塔 把小的放到C上、再中到B上、再小到中上 和 小到A上、再中到大上、再小到中上 这两个步骤只是重复了上面二阶汉诺塔排列的操作
假设把大盘看做是不可移动的(底座),那么以移动大盘到C为分割、前一半的步骤只是将B杆当作了目标区,通过缓冲区C把A的盘子移动到了B上;而后一半的动作同理、只是又把C当作了目标区,而把A当作了缓冲区。
用数学方法表示出来就是:
a3 = a2 + 1 + a2
后面四阶同理:
(图片来自维基百科)
可以表示出来是:
a4 = a3 + 1 + a3
通过数学归纳法我们可以很轻易得到这样的方程:
好了,上面就是汉诺塔的底层数学逻辑,现在默认你已经理解(已经掰的够碎了,不会的建议静下心来再看一遍、动手画一画)
接下来就是我们的算法实现过程了:
首先,汉诺塔在只有一个盘子也就是 n = 1 的情况下是没有考虑意义的,这时候它只需要一个步骤、并为后续排序提供奠基值,即递归出口;
而当n到了2以上时,它便已经符合我们总结出的那个规则了,我们需要写一个递归的函数来实现它
具体来说、先让它传入三个参数,分别是 起始区、缓冲区和目标区 ,
void hannoi (int n, char A, char B, char C) // 起始盘、缓冲盘、目标盘 第一轮主函数传入A、B、C;
如果 n = 1 ,便有这样的输出 :
if (n == 1)
cout << "移动圆盘" << n << "从" << A << "到" << C << endl; 而当 n > 1时,便执行刚刚的三个操作:
1.把B当目标区、从A到B迭代上一轮的操作
2.移动最底下的底盘到C
3.把C当目标区,从B再到C迭代上一轮的操作
写出C++就是:
{
hannoi (n-1, A, C, B); // 把N-1个圆环从起点盘移动到(当前)没有任何圆环的过度盘;通过B、C盘在此函数调用中调用位置的互换,来实现把N-1个圆环从A盘到B盘的转移【A → B】。
cout << "移动圆盘" << n << "从" << A << "到" << C << endl; //底盘挪到C
hannoi (n-1, B, A, C); //通过A、B盘在此函数调用中位置的互换,来实现N-1个圆环从B盘到C盘的转移【B → C】。
}
整体C++代码:
#include
using namespace std;
void hannoi (int n, char A, char B, char C) // 起始盘、缓冲盘、目标盘
{
if (n == 1){
cout << "移动圆盘" << n << "从" << A << "到" << C << endl; //把最后一个圆环从起始盘移动到目标盘。
}
else{
hannoi (n-1, A, C, B); // 把N-1个圆环从起点盘移动到(当前)没有任何圆环的过度盘;通过B、C盘在此函数调用中调用位置的互换,来实现把N-1个圆环从A盘到B盘的转移【A → B】。
cout << "移动圆盘" << n << "从" << A << "到" << C << endl;
hannoi (n-1, B, A, C); //通过A、B盘在此函数调用中位置的互换,来实现N-1个圆环从B盘到C盘的转移【B → C】。
}
}
int main()
{
int n;
cin >> n;
hannoi (n, 'a', 'b', 'c');
return 0;
}
(中间有一次在刷智慧树的时候油猴自动更新、网页卡死、、前面半天都白写了、、、生理性头痛 感觉自己可能先要生天了...)
-------------------------(原文)
首先、三个会吧?
小、中、大
小到A上、中到B、小到中上、大到C上、小到A上、中到大上、小到中上。
也就是小到目标上、中到缓冲上、小到中上、大到目标上、小到初始位置、中到大上、小到中上。
这样。
...三个都想不出来的话......
那两个总不可能不会了吧???
小挪到缓冲上、大挪到目标上、小挪到大上
???
三个就假设是两个的进阶版、先把中间当目标位置,都挪到中间、再把大的挪到右面,然后(现在中间是起始位置)目标换回右面、把中间的挪到右面
四个和两个变三个的做法一样、 都挪到中间、大的挪右边、再以左边的为缓冲从中间往右挪实现方法:
#include
using namespace std;
void hannoi (int n, char A, char B, char C) // 起始盘、缓冲盘、目标盘
{
if (n == 1){
cout << "移动圆盘" << n << "从" << A << "到" << C << endl; //把最后一个圆环从起始盘移动到目标盘。
}
else{
hannoi (n-1, A, C, B); // 把N-1个圆环从起点盘移动到(当前)没有任何圆环的过度盘;通过B、C盘在此函数调用中调用位置的互换,来实现把N-1个圆环从A盘到B盘的转移【A → B】。
cout << "移动圆盘" << n << "从" << A << "到" << C << endl;
hannoi (n-1, B, A, C); //通过A、B盘在此函数调用中位置的互换,来实现N-1个圆环从B盘到C盘的转移【B → C】。
}
}
int main()
{
int n;
cin >> n;
hannoi (n, 'a', 'b', 'c');
return 0;
} python实现:
def move(n,a,b,c):
if n==1:
print(a,'->',c)
else:
move(n-1,a,c,b)
move(1,a,b,c)
move(n-1,b,a,c)
------
再不懂随时欢迎留言、保证一一解答