python实现AdaBoost算法
★ AdaBoost的理解:
对于二分类而言,我们通过一个阈值threshVal将数据集划分为两种分类(正类和负类),而这个阈值就是我们所说的分割线,只不过它总是平行于坐标轴(因为我们取的基分类器是单层决策树):
对于上述数据集,一个基分类器即可将其分类,但是对于大多数训练集而言,一个基分类器是不足够的,比如:
在图3中,我们找不到一条平行于坐标轴的直线将数据集正确的划分,因此我们使用了3个基分类器将其分开,由图4看出,3个分类器把数据集分成6个部分,每一部分我们公式
计算出来它是正类还是负类,比如对第①部分:
,所以第①部分是负类(蓝色点就是负类),再比如第⑥部分:
,所以第⑥部分是正类(红色点就是正类)。依次计算这6个部分,画出图来就是:
由图我们可以看出,橘红色部分(②,③,⑥)是正类,绿色部分(①,④,⑤)是负类。
★ AdaBoost 分类器简介:
adaboost 就是把几个弱分类器,通过线性组合,组合成强分类器,它在训练集上有很高的准确率,但是在测试集上效果却没有那么好,因为它是逐步优化分错的样本,所以最终分类误差率会降到很低,这个组合分类器的数学描述是:
①
其中m是分类器个数,也就是当组合m个弱分类器后,误差率能满足我们的要求。
代表着该分类器的重要程度。
★ AdaBoost 算法流程:
(1) 初始化权值,每一个训练样本最开始时都被赋予相同的权值:1/N (N是样本个数),它代表着开始时每个样本的重要性都是相等的。
我们经过每一次的迭代,上述权值会不断变化,但初始时各权值是相等的。
(2) 使用具有权值分布
的训练数据集学习,得到基本分类器(分类器可以选择SVM,决策树等,后面我们选择最简单的单层决策树作为基分类器):
这里
就是第m个基分类器,它的取值只有-1或者+1。
(3) 计算
在训练集上的分类误差率:
其中:
是第m个分类器
的分类误差率,就是分类器
分错的概率。
是第m个分类器
在数据集x上使用的每个样本的权值,跟公式②的
一个意思
是第m个分类器对第i个样本的预测分类。它的取值是-1或+1
是第i个样本真实的分类。对于二分类来说,它的取值也是-1或+1
当括号里面条件为true的时候取值为1,反之,为false的时候取值为0,这里
可不是单位矩阵哈
(4) 计算
的系数
,
代表着该分类器的重要程度,当这个分类器的分类误差率越低的时候,
就越大。
从上式④可以看出,分类误差率
越小,
就越大,对应的分类器就越重要。
(5) 更新每个样本的权值:
其中:
是第m+1个分类器的各样本点权值分布
是第m+1个分类器的样本点权值的更新规则。
是归一化因子,他其实就是分子的和。
⑥
上式的公式⑥是有公式③、④代入得到的。
(6) 线性组合各弱分类器:
得到最终的分类器:
★ AdaBoost 算法的解释:
证明 AdaBoost 的损失函数是指数函数:(可通过前向分布算法来推adaboost,只要证明前向分布算法与adaboost都是加法模型,并当前向分布算法取指数损失函数时就是adaboost,那么就证明了adaboost使用的是指数损失函数)
✿ 首先我们先来看一下前向分布算法:
前向分布算法的加法模型是:
其中,
为基函数,
为基函数的参数,
为基函数的系数,M是基分类器个数由公式⑦可以看出,adaboost也是一个加法模型。
假设前向分布算法的损失函数是
,那么算法的目标函数就是极小化损失函数:
⑩
上式中的N是样本个数。
前向分布算法求解这一优化问题的思想是:因为该学习是加法模型,如果能够从前向后,每一步只学习一个基函数及其系数,逐步逼近优化目标函数式⑩,那么就可以简化该优化问题的复杂度,因此每一步只需优化如下损失函数(即优化每一个基分类器的损失函数):
⑪
当前向分布算法的损失函数
是指数损失函数时,即:
⑫
只需证明该学习的具体操作等价于AdaBoost的具体操作,就可证明AdaBoost也使用的是指数损失函数。假设我们经过m-1次迭代前向分布算法得到
:
⑬
在第m轮迭代得到
,
和
:
⑭
目标是使前向分布算法得到的
和
使得
在训练集上的指数损失函数最小,即:
公式⑮可以表示为:
其中:
。 因为
既不依赖
也不依赖于G,所以与最小化无关。但
依赖于
,随着每一轮迭代而发生改变。
现证使公式⑯达到最小时,
,
,
的取值就是AdaBoost算法得到的
,
,
。
对于任意
,使公式最小的
由下式得到:
⑰
我们要求极小值,所以将上式对
求偏导并令其为0:
⑱
而AdaBoost的
为:
对比公式③、⑲可以看出,AdaBoost的
和前向分布算法的
是一致的。
故求导的原式为:
解上式得:
而AdaBoost的
:
对比公式④、⑳可以看出,AdaBoost的
和前向分布算法的
是一致的。
我们再来推算前向分布算法的每个样本的权值更新,由公式:
㉑
将公式㉑的第一个式子,等式两边同时乘以 -y 再取以e为底数:
㉒
对比公式⑤、㉒,可以看出AdaBoost的
和前向分布算法的
只差一个归一化因子,因而等价。
因此,AdaBoost算法使用的是指数损失函数。
★ 代码实践:
from numpy import * import matplotlib.pyplot as plt import matplotlib from matplotlib.font_manager import * def loadDataSet(): # 加载测试数据 dataMat = mat([[1.,2.1], [1.5,1.6], [1.3,1.], [1.,1.], [2.,1.], [1.1,1.2]]) labelList = [1.0,1.0,-1.0,-1.0,1.0] return dataMat, labelList # 数据集返回的是矩阵类型,标签返回的是列表类型 def stumpClassify(dataMat,dimen,threshVal,threshIneq): # dimen:第dimen列,也就是第几个特征, threshVal:是阈值 threshIneq:标志 retArray = ones((shape(dataMat)[0],1)) # 创造一个 样本数×1 维的array数组 if threshIneq == 'lt': # lt表示less than,表示分类方式,对于小于等于阈值的样本点赋值为-1 retArray[dataMat[:,dimen] <= threshVal] = -1.0 else: # 我们确定一个阈值后,有两种分法,一种是小于这个阈值的是正类,大于这个值的是负类, #第二种分法是小于这个值的是负类,大于这个值的是正类,所以才会有这里的if 和else retArray[dataMat[:,dimen] > threshVal] = -1.0 return retArray # 返回的是一个基分类器的分类好的array数组 def buildStump(dataArr,classLabels,D): dataMat = mat(dataArr) labelMat = mat(classLabels).T m,n = shape(dataMat) numStemp = 10 bestStump = {} bestClassEst = mat(zeros((m,1))) minError = inf # 无穷 for i in range(n): # 遍历特征 rangeMin = dataMat[:,i].min() # 检查到该特征的最小值 rangeMax = dataMat[:,i].max() stepSize = (rangeMax - rangeMin)/numStemp # 寻找阈值的步长是最大减最小除以10,你也可以按自己的意愿设置步长公式 for j in range(-1, int(numStemp)+1): for inequal in ['lt', 'gt']: # 因为确定一个阈值后,可以有两种分类方式 threshVal = (rangeMin+float(j) * stepSize) predictedVals = stumpClassify(dataMat,i,threshVal,inequal) # 确定一个阈值后,计算它的分类结果,predictedVals就是基分类器的预测结果,是一个m×1的array数组 errArr = mat(ones((m,1))) errArr[predictedVals==labelMat] =0 # 预测值与实际值相同,误差置为0 weightedEroor = D.T*errArr # D就是每个样本点的权值,随着迭代,它会变化,这段代码是误差率的公式 if weightedEroor★ 运行结果:
★ 推算上述填充颜色的规律(以至于写出填充颜色的代码):
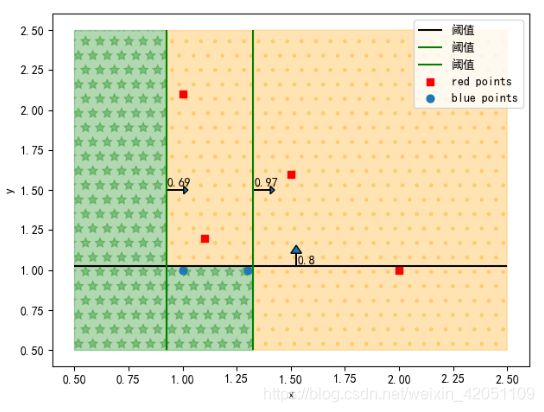
不失一般性,我们随便举一个例子如上图7,共有3条纵向阈值,2条横向阈值,将信息绘制成表格:
纵向阈值 0.4 0.6 0.8 分类方式 gt lt lt
横向阈值 1.2 1.0 分类方式 gt lt 注意:纵向阈值(竖线)按从小达到排序,横向阈值(横线)按从大到小排序,至于原因,可以看图7就知道了。
gt和lt对应上文的两种分类方式,gt箭头就朝左,lt箭头就朝右。可以看出,这3条竖线和2条横线把该区域分成了12个部分,这里分成的区域数就是: (横线条数+1)×(竖线条数+1)。
现在我们判别每一部分是正类还是负类,可以写出每一部分的计算公式,比如我先写出①②③④这个四个部分的计算公式:
①
当然了,上述式子是通过人观察图7,根据箭头指向来判断出加减号,然后写出来的计算式子。那么如何通过代码来代替人的观察以此来写出加减号呢?
其实加号或减号在代码中的体现就是+1或-1。我们把(1.),(2.),(3.),(4.)的符号提出来观察一下:
我把式子③分成左右两部分了(因为左边是竖线阈值提出来的符号,右部分是横线阈值提出来的符号)。gt和lt是字母表示的是分类方式,字母我们不能用于计算,所以我们规定:lt为+1,而gt为-1。(当然这是我自己规定的,你也可以反过来)。因此3条竖线阈值可以写为[-1,1,1],而2条横线阈值可以写为[-1,1]。
我们再来看图7,每一部分都跟这3条竖线和2条横线有关系,比如第①部分:它在竖线阈值0.4的左边,在竖线阈值0.6的左边,在竖线阈值0.8的左边,在横线阈值1.2的上边,在横线阈值1.0的上边。现在我们再次规定:在直线右边或上边的部分为+1,在直线左边或下边的部分为-1。因此由刚才叙述的第①部分与各直线的关系,我们可以写出来第①部分和3条竖线阈值的关系是[-1,-1,-1],与2条横线阈值的关系是:[1,1]。我们把阈值与区域和阈值的关系进行点乘(竖线和横线要分开,然后再合起来),比如还是第①部分:
④
上式④的+号是合并列表的意思,不是加减乘除的+号。对比式子③,可以看出与式子③的第一个式子一致,因此这样考虑是可行的,不信的话,可以根据上述规则写出第②部分的计算式子:
⑤
再把⑤和式子③的第二个式子对比,发现还是一致,现在小伙伴们可以相信这个做法是正确的。
可是还有一个问题:上述区域与竖线阈值(或横线阈值)的关系而写出的表达式使我们用肉眼看出来的,比如你看到第①部分在竖线阈值0.4的左边,你才根据规则写出的-1,可是程序不会肉眼看啊,现在我们再来发现一个规律:先把这些位置关系的表达式写出来,看看有没有规律可循,比如我先把①②③④这个四个区域与竖线阈值的关系写出来,你可以看出端倪:
我们可以看出第一行0个1,3个-1,而第二行1个1,2个-1,第三行2个1,1个-1,第四行3个1,0个-1。而在写代码时,我们遍历行的时候,就是遍历①②③④这四个部分来填充颜色,不正是第①部分j=0;第②部分j=1;第③部分j=2;第④部分j=3。那么上面矩阵的每一行就可以这么来制造,伪代码就是:
for j in range(竖线阈值的条数+1): # 因为看图7,第一行不正好4部分,对应区域①②③④
row_list = [1]*j + [-1]*(竖线阈值的条数)
同样的方法,我们也可以写出①⑤⑨这个3个区域与横线阈值的关系(为啥不继续写①②③④与横线的关系,因为①②③④与横线的关系是一样的,①⑤⑨在图7中是不同列的,他们的关系才是不同的):
我们同样看出了端倪:第一行0个-1,2个1;第二行1个-1,1个1;第三行2个-1,0个1。这正是我们写代码时遍历列,第一列 i = 0,第二列 i=1,第三列 i=2,因此伪代码是:
for i in range(横线阈值的条数+1):
column_list = [-1]*i + [1]*(横线阈值的条数)
因此我们把遍历行和遍历列的伪代码拼在一起,成为遍历3×4个区域,依次填充颜色。
✿ 我们写成伪代码(代码里的+号都是合并列表的意思,不是加减乘除的+号):
for i in range(横线阈值的条数+1):
for j in range(竖线阈值的条数+1):
symbol_list = row_list = [1]*j + [-1]*(竖线阈值的条数) + column_list = [-1]*i + [1]*(横线阈值的条数)
result = sign([alpha值的列表]*symbol_list):
if reslut == 1:
正类(红点)
else:
负类(蓝点)
★ 参考链接:
1. http://www.cnblogs.com/Tang-tangt/p/9557089.html
2. https://zhuanlan.zhihu.com/p/30035094
3. 统计学习与方法, 李航 P138-P146




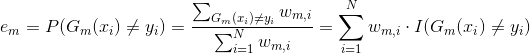
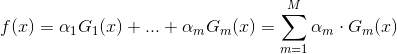
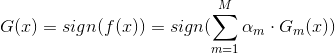
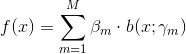
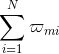
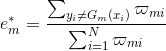


![\begin{matrix} [-1,-1,-1]\\ [\; \; \: 1,-1,-1] \\ [\; \; \: 1,\; \; \: 1,-1] \\ [\; \; \: 1,\; \; \: 1,\; \; \: 1] \end{matrix}](http://img.e-com-net.com/image/info8/42ed457a897f43b3a93ff60a2b6c2b4f.gif)
![\begin{matrix} [\; \; \: 1,\; \; \: 1]\\ [-1,\; \; \: 1] \\ [-1,-1] \end{matrix}](http://img.e-com-net.com/image/info8/4e8db742194544fc897b392fa6db0c97.gif)