LeetCode刷题笔记（10）-BFS广度优先搜索

LeetCode刷题笔记（10）-BFS广度优先搜索

BFS模板：
void BFS()
{
    定义队列;
    定义备忘录，用于记录已经访问的位置；

    判断边界条件，是否能直接返回结果的。

    将起始位置加入到队列中，同时更新备忘录。

    while (队列不为空) {
        获取当前队列中的元素个数。
        for (元素个数) {
            取出一个位置节点。
            判断是否到达终点位置。
            获取它对应的下一个所有的节点。
            条件判断，过滤掉不符合条件的位置。
            新位置重新加入队列。
        }
    }

}

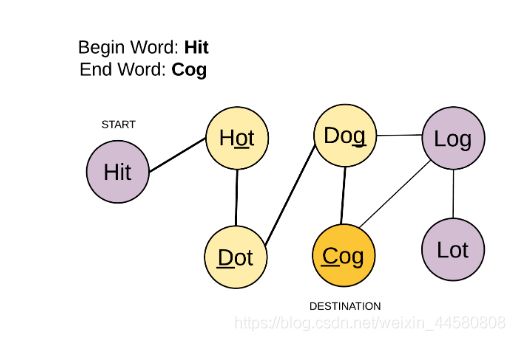
127、单词接龙

给定两个单词（beginWord 和 endWord）和一个字典，找到从 beginWord 到 endWord 的最短转换序列的长度。转换需遵循如下规则：

• 每次转换只能改变一个字母。
• 转换过程中的中间单词必须是字典中的单词。
• 输入:
• beginWord = “hit”,
• endWord = “cog”,
• wordList = [“hot”,“dot”,“dog”,“lot”,“log”,“cog”]
• 输出: 5
• 解释: 一个最短转换序列是 “hit” -> “hot” -> “dot” -> “dog” -> “cog”,

•  返回它的长度 5。
  

// A code block
解题思路：
我们将问题抽象在一个无向无权图中，每个单词作为节点，
差距只有一个字母的两个单词之间连一条边。
问题变成找到从起点到终点的最短路径，
如果存在的话。因此可以使用广度优先搜索方法。
算法中最重要的步骤是找出相邻的节点，也就是只差一个字母的两个单词。
为了快速的找到这些相邻节点，我们对给定的 wordList 做一个预处理，
将单词中的某个字母用 * 代替。
这个预处理帮我们构造了一个单词变换的通用状态。
例如：Dog ----> D*g <---- Dig，Dog 和 Dig 都指向了一个通用状态 D*g。

这步预处理找出了单词表中所有单词改变某个字母后的通用状态，
并帮助我们更方便也更快的找到相邻节点。
否则，对于每个单词我们需要遍历整个字母表查看
是否存在一个单词与它相差一个字母，这将花费很多时间。
预处理操作在广度优先搜索之前高效的建立了邻接表。
算法：
对给定的 wordList 做预处理，找出所有的通用状态。
将通用状态记录在字典中，键是通用状态，值是所有具有通用状态的单词。
将包含 beginWord 和 1 的元组放入队列中，1 代表节点的层次。
我们需要返回 endWord 的层次也就是从 beginWord 出发的最短距离。
为了防止出现环，使用访问数组记录。
当队列中有元素的时候，取出第一个元素，记为 current_word。
找到 current_word 的所有通用状态，
并检查这些通用状态是否存在其它单词的映射，
这一步通过检查 all_combo_dict 来实现。
从 all_combo_dict 获得的所有单词，都和 current_word 共有一个通用状态
，所以都和 current_word 相连，因此将他们加入到队列中。
对于新获得的所有单词，向队列中加入元素 (word, level + 1) 
其中 level 是 current_word 的层次。
最终当你到达期望的单词，对应的层次就是最短变换序列的长度。

 public static int ladderLength(String beginWord, String endWord, List<String> wordList) {
     
        // 给定单词列表中不包括endword，直接返回
        if (!wordList.contains(endWord)) return 0;
        // 题目说明，每个单词长度相同
        int len = beginWord.length();
        // 处理给出的单词字典，转换为全部的通用状态及每个通配词映射的单词集合
        HashMap<String, ArrayList<String>> allComboDict = new HashMap<>();
        // lambda表达式遍历，currWord是当前正在遍历的单词
        wordList.forEach(curWord -> {
     
            // 每个单词能得到len种通配词(每个位置字符都可变为*)
            for (int i = 0; i < len; i++) {
     
                // 得到通配词
                String comboWord = curWord.substring(0, i) + "*" + curWord.substring(i + 1, len);
                // 从通配字典全集中拿到这个通配词对应的单词集合，如果是空(第一次得到通配词时)就创建一个新的
                ArrayList<String> comboWordList = allComboDict.getOrDefault(comboWord, new ArrayList<>());
                // 把当前这个单词加进去，因此从这个单词得到了这个通配词
                comboWordList.add(curWord);
                // 更新一个通配字典全集中这个通配词对应的单词集合
                allComboDict.put(comboWord, comboWordList);
            }
        });
        // 广度优先遍历队列
        // LinkedList implements Deque extends Queue
        Queue<Pair<String, Integer>> queue = new LinkedList<>();
        // 记录已遍历过的单词,为什么不用List，因为之后判断节点是否已遍历过时，ArrayList的contains方法太低效了，它的底层是数组，或者直接用TreeSet也可以
        // ArrayList hasVistedList = new ArrayList<>();
        HashMap<String, Boolean> hasVistedList = new HashMap<>();
        // 开始词作为第一个节点加入队列,深度level是1，标记其已访问
        queue.add(new Pair<>(beginWord, 1));
        // hasVistedList.add(beginWord);
        hasVistedList.put(beginWord, true);
        // 广度优先遍历，逐个取出队列中元素进行操作
        while (!queue.isEmpty()) {
     
            // 队列第一个节点
            Pair<String, Integer> node = queue.remove();
            // 当前节点对应的<单词，层级>
            String currWord = node.getKey();
            int level = node.getValue();
            for (int i = 0; i < len; i++) {
     
                // 从当前单词，得到len个通配词
                String currComboWord = currWord.substring(0, i) + "*" + currWord.substring(i + 1, len);
                // 拿到这个通配词映射的单词集合(也就是从当前单词一次转换能得到哪些单词)
                ArrayList<String> currComboWordList = allComboDict.getOrDefault(currComboWord, new ArrayList<>());
                // 遍历其中是否包含目标单词
                for (String word : currComboWordList) {
     
                    // 包含目标单词，说明当前单词能一次转换到目标单词，经历的步骤数是当前单词的层级 + 1
                    if (word.equals(endWord))
                        return level + 1;
                    // 否则，当前单词能得到这个单词，如果它还没被访问过
                    // if (!hasVistedList.contains(word)){
     
                    // HashMap.containsKey方法效率远高于ArrayList.contains
                    if (!hasVistedList.containsKey(word)){
     
                        // 把这个单词加入到队列中
                        queue.add(new Pair<>(word, level + 1));
                        // 标记它为已访问
                        // hasVistedList.add(word);
                        hasVistedList.put(word, true);
                    }
                }
            }
        }
        return 0;
    }
}

总结：BFS的思想就在于层级的概念，这道题比较难，
合理运用了HashMap的特点，理解起来还是比较费劲的，这道题多看看。

279、完全平方数

• 给定正整数 n，找到若干个完全平方数（比如 1, 4, 9, 16, …）使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
• 示例 1:
• 输入: n = 12
• 输出: 3
• 解释: 12 = 4 + 4 + 4.

解题思路：
正如上述贪心算法的复杂性分析种提到的，调用堆栈的轨迹形成一颗 N 元树，
其中每个结点代表 is_divided_by(n, count) 函数的调用。基于上述想法，
我们可以把原来的问题重新表述如下：

给定一个 N 元树，其中每个节点表示数字 n 的余数减去一个完全平方数的组合，
我们的任务是在树中找到一个节点，该节点满足两个条件：

(1) 节点的值（即余数）也是一个完全平方数。
(2) 在满足条件（1）的所有节点中，节点和根之间的距离应该最小。
算法：

首先，我们准备小于给定数字 n 的完全平方数列表（即 square_nums）。
然后创建 queue 遍历，该变量将保存所有剩余项在每个级别的枚举。
在主循环中，我们迭代 queue 变量。在每次迭代中，
我们检查余数是否是一个完全平方数。如果余数不是一个完全平方数，
就用其中一个完全平方数减去它，得到一个新余数，
然后将新余数添加到 next_queue 中，
以进行下一级的迭代。一旦遇到一个完全平方数的余数，
我们就会跳出循环，这也意味着我们找到了解。
在典型的 BFS 算法中，queue 变量通常是数组或列表类型。
但是，这里我们使用 set 类型，以消除同一级别中的剩余项的冗余。
事实证明，这个小技巧甚至可以增加 5 倍的运行加速。

public class numSquares279 {
     
    public int numSquares(int n ) {
     
        ArrayList<Integer> square_nums = new ArrayList<>();
        for (int i = 1; i * i <= n; i++) {
     
            square_nums.add(i * i);
        }

        Set<Integer> queue = new HashSet<Integer>();
        queue.add(n);
        int level = 0;
        while (queue.size() > 0) {
     
            level += 1;
            Set<Integer> next_queue = new HashSet<Integer>();

            for (Integer remainder : queue) {
     
                for (Integer square : square_nums) {
     
                    if (remainder.equals(square)) {
     
                        return level;
                    } else if (remainder < square) {
     
                        break;
                    } else {
     
                        next_queue.add(remainder - square);
                    }
                }
            }
            queue = next_queue;
        }
        return level;
    }
}

这道题目用了两层循环，对队列中的每个数字进行遍历，
以可能满足条件的square_nums寻找下一层。

1091、最短路径

• 在一个 N × N 的方形网格中，每个单元格有两种状态：空（0）或者阻塞（1）。
• 一条从左上角到右下角、长度为 k 的畅通路径，由满足下述条件的单元格 C_1, C_2, …, C_k 组成：
• 相邻单元格 C_i 和 C_{i+1} 在八个方向之一上连通（此时，C_i 和 C_{i+1} 不同且共享边或角）
• C_1 位于 (0, 0)（即，值为 grid[0][0]）
• C_k 位于 (N-1, N-1)（即，值为 grid[N-1][N-1]）
• 如果 C_i 位于 (r, c)，则 grid[r][c] 为空（即，grid[r][c] == 0）

解题思路：
要找到左上角到右下角的最短路径，最短路径嘛，自然就想到了使用BFS。
在二维平面上，八个方向可以进行移动，使用int[][] directions表示八个方向。比如{1,1}就表示右下方向。二维平面常规做法，使用函数boolean inGrid(int x, int y)判断某个点是否在矩形范围内（防止数组越界）。
首先将成员变量，表示矩形行列数的row, col初始化。然后如果左上角或者右下角为1，一定无法从左上角到右下角，直接返回-1。
然后开始使用队列模拟BFS：
我们需要去判断哪些路径已经走过，并且我们还需要知道走到某一个点时的步数，结合题目规定0是通行，1是不可通行，走过的点也不会再走相当于不可通行。所以我们可以用grid[newX][newY] == 0表示没有访问过的可通行的点。
按照题意，起点也有长度1，所以设置grid[0][0] = 1;，且 pos.add(new int[]{0,0});。
用队列模拟的循环条件!pos.isEmpty() && grid[row - 1][col - 1] == 0，第二个条件不满足时，说明已经有路径到达右下角了，就可以停止搜索。
弹出某个点的坐标，通过int preLength = grid[xy[0]][xy[1]];得到到达该点的长度，然后遍历8个方向，试图访问下一个点，满足inGrid(newX, newY) && grid[newX][newY] == 0则可以访问，然后到达下一个点的路径长度就变为grid[newX][newY] = preLength + 1;，然后这个点grid[newX][newY] != 0了，就不会被重复访问。
循环结束后，可能是搜索完成但没有到达右下角，此时grid[row - 1][col - 1] == 0；也可能是已经找到到达右下角的路径，按BFS，此时grid[row - 1][col - 1]即为答案。所以最后返回grid[row - 1][col - 1] == 0 ? -1 : grid[row - 1][col - 1];
时间复杂度为O(n)O(n)，因为每个元素遍历了一次，n为元素的个数。空间复杂度为O(k)O(k)，k为过程中队列的最大元素个数。

public class shortestPathBinaryMatrix1091 {
     
   public int shortestPathBinaryMartix(int[][] grids){
     
       if(grids==null || grids.length==0 || grids[0].length==0){
     
           return -1;
       }
       int[][] direction = {
     {
     1,-10}, {
     1,1},{
     0,-1},{
     -1,-1},{
     -1,0},{
     -1,1}};
       int m = grids.length,n=grids[0].length;//二维矩阵取行与列的方法
       Queue<Pair<Integer,Integer>> queue = new LinkedList<>();
       queue.add(new Pair<>(0,0));
       int pathLength = 0;
       while (!queue.isEmpty()){
     
           int size = queue.size();
           pathLength++;
           while(size-- > 0){
     
               Pair<Integer,Integer> cur = queue.poll();
               int cr = cur.getKey(), cc = cur.getValue();
               if(grids[cr][cc]==1) continue;
               if(cr == m-1 && cc == n-1) return pathLength;
               grids[cr][cc] = 1;
               for(int[] d :direction){
     
                   int nr = cr + d[0], nc = cc + d[1];
                   if(nr < 0 || nr >= m || nc < 0 || nc >= n){
     
                       continue;
                   }
                   queue.add(new Pair<>(nr,nc));
               }
           }
       }
       return -1;
   }
}

这道题我理解的不是很好，不过我发现Pair<>键值对在这几道题中重复使用。
这道题目还有一个值得学习的点就是二维数组的处理，特点的在遍历完某一个点之后令grids[cr][cc] = 1;