DFS、BFS与回溯法
目录
- 基本概念
- 通用模板
- 例子
-
- Leetcode 257. Binary Tree Paths(easy)
- Leetcode 107. Binary Tree Level Order Traversal II(easy)
- Leetcode 40. Combination Sum II(medium)
- Leetcode 199. Binary Tree Right Side View(medium)
-
- dfs解法
- bfs解法
- Leetcode 133. Clone Graph(medium)
-
- bfs解法
- dfs解法
- Leetcode 207. Course Schedule(medium)
-
- dfs解法
- bfs解法
- Leetcode 99. Recover Binary Search Tree(hard)
基本概念
深度优先搜索,一种用于遍历或搜索树或图(树是特殊的图)的算法。 优先沿着树的深度遍历树的节点,尽可能深的搜索树的分支。
广度优先搜索,优先遍历当前节点的所有子节点,再逐层向下遍历。通常需要使用队列进行辅助。
回溯法,本质上就是dfs的思想,可以说是dfs的一种应用,主要的区别在于回溯法需要显式地删除当前步骤的结果,回退至上一步。
通用模板
void dfs(Node node){
if(满足节点条件)
return;
// 对该节点进行操作
doSomething();
// 遍历下一个节点
dfs(node.next);
}
void bfs(Node node){
Queue<Node> q = new LinkedList<>();
q.offer(node);
while(!q.isEmpty()){
Node n = q.poll();
// 对当前节点进行操作
doSomething();
// 将当前节点的子节点加入队列中
q.offer(n.子节点);
}
}
void backtracking(Node node){
if(满足节点条件)
return;
// 对该节点进行操作
doSomething();
// 遍历下一个节点
backtracking(node.next);
// 删除当前结果
deleteNow();
}
例子
Leetcode 257. Binary Tree Paths(easy)
题目描述

分析:因为要输出所有的路径,因此适合采用dfs,每次遍历一条路径,在遍历过程中,需要记录下每一个节点,当遍历到叶节点时存入到结果链表中即可。
class Solution {
// 用于保存结果
private List<String> list = new ArrayList<>();
public List<String> binaryTreePaths(TreeNode root) {
dfs(root, "");
return list;
}
private void dfs(TreeNode root, String s){
// 边界条件
if(root == null)
return;
// doSomething()
// 保存下每个节点
StringBuffer sb = new StringBuffer(s);
if(sb.length() == 0)
sb.append(root.val);
else
sb.append("->").append(root.val);
// 到达叶结点时
if(root.left == null && root.right == null){
list.add(sb.toString());
return;
}
// 遍历下一个节点
if(root.left != null)
dfs(root.left, sb.toString());
if(root.right != null)
dfs(root.right, sb.toString());
}
}
Leetcode 107. Binary Tree Level Order Traversal II(easy)
题目描述

分析:因为题目要求按层输出结果,所以优先想到使用bfs进行搜索。题目要求最后结果需从下向上,则在输出链表中将答案插在链表头部即可。
class Solution {
public List<List<Integer>> levelOrderBottom(TreeNode root) {
List<List<Integer>> res = new LinkedList<>();
if(root == null)
return res;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
List<Integer> list = new ArrayList<>();
// 按层处理
int n = queue.size();
while(n-- != 0){
TreeNode node = queue.poll();
if(node != null){
list.add(node.val);
queue.add(node.left);
queue.add(node.right);
}
}
if(!list.isEmpty())
res.add(0,list);
}
return res;
}
}
Leetcode 40. Combination Sum II(medium)
题目描述

分析:因为对于每一个target都需要遍历一下candidates数组,而当前candidates的值与下一个值之间没有关系,因此需要删除链表中当前的结果,即回溯的思想。
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
Arrays.sort(candidates);
List<List<Integer>> res = new ArrayList<>();
backtrack(candidates, target, 0, res, new ArrayList<>());
return res;
}
private void backtracking(int[] candidates, int target, int start, List<List<Integer>> res, List<Integer> list){
if(target < 0)
return;
if(target == 0){
res.add(new ArrayList<Integer>(list));
return;
}
for(int i = start; i < candidates.length; i++){
if(i > start && candidates[i] == candidates[i-1])
continue;
int num = candidates[i];
list.add(num);
backtracking(candidates, target-num, i+1, res, list);
// deleteNow();
list.remove(list.size()-1);
}
}
}
Leetcode 199. Binary Tree Right Side View(medium)
dfs解法
分析:因为输出的是每一行最右边的节点,因此从根节点的右节点开始往下遍历,每一个右节点的右节点就是我们所需要的,如果右节点缺失,则将左节点保存下来。
class Solution {
private List<Integer> list = new ArrayList<>();
public List<Integer> rightSideView(TreeNode root) {
dfs(root, 1);
return list;
}
// index用于记录下一个需要保存的是树中的第几行
private void dfs(TreeNode root, int index){
// 边界条件
if(root == null)
return;
// doSomething()
// 满足该条件,说明是最右边的节点,否则是该行的其他节点,则不需要保存
if(list.size() < index)
list.add(root.val);
// 遍历下一个节点
dfs(root.right, index+1);
dfs(root.left, index+1);
}
}
bfs解法
分析:相比dfs的解法,bfs更容易优先想到,因为题目要求是按行输出。输出最右侧的节点,则只需要从左节点遍历,取出队列最后一个元素,或者从右节点遍历,取出队列第一个元素。
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> res = new ArrayList<>();
if(root == null)
return res;
LinkedList<TreeNode> q = new LinkedList<>();
q.add(root);
while(!q.isEmpty()){
res.add(q.getLast().val);
int n = q.size();
for(int i = 0; i <n; i++){
TreeNode node = q.poll();
if(node.left != null)
q.add(node.left);
if(node.right != null)
q.add(node.right);
}
}
return res;
}
}
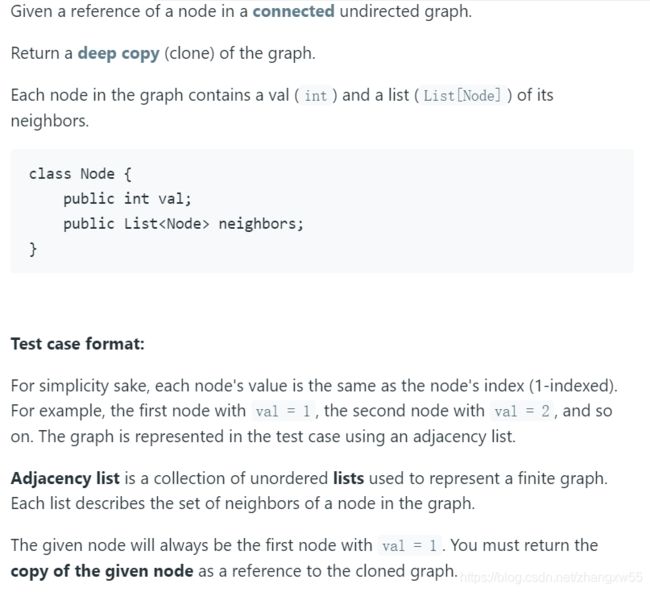
Leetcode 133. Clone Graph(medium)
bfs解法
分析:主要思想就是将当前节点的相邻节点放入队列中,依次遍历复制。但考虑到会出现使用散列表来记录值和节点之间的关系,只需要将未存在的相邻节点加入队列即可,对于已经存在的节点,可以通过散列表直接访问。
class Solution {
// bfs
public Node cloneGraph(Node node) {
if(node == null)
return null;
Node copy = new Node(node.val);
HashMap<Integer, Node> map = new HashMap<>();
map.put(copy.val, copy);
Queue<Node> q = new LinkedList<>();
q.add(node);
while(!q.isEmpty()){
Node n = q.poll();
// 遍历当前节点的所有相邻节点
for(Node neighbor : n.neighbors){
if(!map.containsKey(neighbor.val)){
map.put(neighbor.val, new Node(neighbor.val));
q.add(neighbor);
}
// 复制节点
map.get(n.val).neighbors.add(map.get(neighbor.val));
}
}
return copy;
}
}
dfs解法
分析:大致思想与bfs相同,但是搜索方式是一直遍历该节点的相邻节点,直到节点为空,或者已经访问过。
class Solution{
private HashMap<Integer, Node> map = new HashMap<>();
public Node cloneGraph(Node node) {
// 边界条件
if(node == null)
return node;
if(map.containsKey(node.val))
return map.get(node.val);
// doSomething()
Node newNode = new Node(node.val);
map.put(node.val, newNode);
for(Node n : node.neighbors){
// dfs
newNode.neighbors.add(cloneGraph(n));
}
return newNode;
}
}
Leetcode 207. Course Schedule(medium)
dfs解法
分析:无论是用哪种方法进行搜索,首先都需要构造出有向图,这里用链表来构造节点之间的方向关系。题目的根本目的就是判断有向图中是否出现环,若出现则返回false,因此用一个布尔数组visited来记录是否访问过该节点,若之前已经访问,则返回false。考虑到公共节点的存在,因此使用boolean数组dp来记录已经访问过的情况。
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
// 构造有向图
ArrayList[] graph = new ArrayList[numCourses];
for(int i = 0; i<numCourses; i++){
graph[i] = new ArrayList();
}
for(int i=0; i<prerequisites.length; i++){
graph[prerequisites[i][1]].add(prerequisites[i][0]);
}
// dfs
boolean[] visited = new boolean[numCourses];
boolean[] dp = new boolean[numCourses];
for(int i=0; i<numCourses; i++){
if(!dfs(graph, i, visited, dp))
return false;
}
return true;
}
private boolean dfs(ArrayList[] graph, int index, boolean[] visited, boolean[] dp){
if(visited[index])
return dp[index];
else
visited[index] = true;
for(int i=0; i<graph[index].size(); i++){
if(!dfs(graph, (int)graph[index].get(i), visited, dp)){
dp[index] = false;
return false;
}
}
dp[index] = true;
return true;
}
}
bfs解法
分析:首先补充一下入度的概念。
入度(in-degree) :以某顶点为弧头,终止于该顶点的弧的数目称为该顶点的入度。
入度为0的节点即有向图中的起点,也就是本题中最先修的课程。在构造有向图时记录下每个节点的入度,然后将入度为0的节点(即起点)放入队列中,使用变量count来记录入度为0的节点数目。每次循环从队列头取一个节点,然后查询该节点的相邻节点,并将其节点的入度-1,每次将入度变为0的节点放入队列中,同时count++。一直循环,直到队列为空。
若该图是拓扑有序的,则所有的节点最终入度都会为0,即count==numCourse,否则说明图中有环,输出false。
class Solution {
public boolean canFinish(int numCourses, int[][] prerequisites) {
ArrayList[] graph = new ArrayList[numCourses];
int[] degree = new int[numCourses];
Queue<Integer> q = new LinkedList<>();
int count = 0;
// 构造有向图
for(int i = 0; i<numCourses; i++){
graph[i] = new ArrayList<Integer>();
}
for(int i=0; i<prerequisites.length; i++){
degree[prerequisites[i][1]]++;
graph[prerequisites[i][0]].add(prerequisites[i][1]);
}
// bfs
for(int i=0; i<degree.length; i++){
if(degree[i] == 0){
q.add(i);
count++;
}
}
while(!q.isEmpty()){
int course = q.poll();
for(int i = 0; i<graph[course].size(); i++){
int pointer = (int)graph[course].get(i);
degree[pointer]--;
if(degree[pointer] == 0){
q.add(pointer);
count++;
}
}
}
return numCourses == count;
}
}
Leetcode 99. Recover Binary Search Tree(hard)
题目描述

分析:目的是要找出平衡二叉树中的两个错误节点,可以采用二叉树的中序遍历,在遍历过程中找到错误节点,最后在主函数中对两个错误节点的值进行交换即可。
class Solution {
TreeNode change1 = null;
TreeNode change2 = null;
TreeNode preElement = new TreeNode(Integer.MIN_VALUE);
public void recoverTree(TreeNode root) {
traverse(root);
// 交换
int tmp = change1.val;
change1.val = change2.val;
change2.val = tmp;
}
private void traverse(TreeNode root){
// 边界条件
if(root == null)
return;
// 遍历下一个节点,doSomething()
traverse(root.left);
if(preElement.val > root.val){
change2 = root;
if(change1 == null){
change1 = preElement;
}else
return;
}
preElement = root;
traverse(root.right);
}
}