计算机系统基础:数据的表示和存储
文章目录
- 数据的表示和存储
- 信息的二进制编码
- 定点数的表示
- C语言支持的基本数据类型
- 编译器处理常量时的默认类型
- 浮点数的表示及范围
- IEEE754
- 非数值数据的编码表示
- 多媒体信息的表示
- 数据宽度和存储容量单位
- 数据的基本宽度
- 数据量的度量单位
- 数据类型宽度
- 数据的存储和排列顺序
数据的表示和存储
信息的二进制编码
数据:
数值数据:无符号整数、有符号整数;浮点数;(可以在数轴上表示出来,可比较大小的)
非数值数据:逻辑数(包括01序列),字符等
计算机内部所有信息都使用二进制进行编码,原因:
- 具有两个稳定态的物理器件容易制造(电位高/低,脉冲有/无,正/负极,表示1和0)
- 二进制编码,计数,运算规则简单,也易于电路实现
- 与逻辑值真/假对应,便于逻辑运算
- 易使用逻辑电路实现二进制算术运算
真值和机器数:
- 机器数:计算机内部用0和1编码的01序列
- 真值:机器数所表示的真实的值
如 char 型变量 c 的真值为-128,其机器数为1000 0000
要确定一个数值数据的值,必须先确定三个要素:
- 进制(最基本的表示方式)
- 定、浮点表示(解决小数点问题)
- 编码方式(解决正负号问题)
进制:
十进制,二进制,八进制,十六进制
定/浮点表示:
计算机中并没有小数点的直接表示,只能约定小数点的位置,
由此产生定点数(定点整数、定点小数),
浮点数(可用一个定点小数和一个定点整数表示,小数点的位置用一个数值表示)
编码方式:
计算机中也没有正负号的直接表示,因此用一位二进制数表示正负,
并且使用原码、补码、反码(少见)、移码等编码方案表示真值
定点数和浮点数
定点数:小数点位置约定在固定位置
浮点数:小数点位置约定为可浮动的数
任何实数X,可以写为 X = (-1)S × M × RE,
其中,S 取值为0或1,决定 X 的符号;M 是一个二进制定点小数,称为数 X 的尾数;
E 是一个二进制定点整数,称为数 X 的阶或指数,指示尾数中的小数点位置;
R 是进制的基数(现代计算机为2,早期为4和16);
只要表示 S、M 和 E 三个信息,就可以确定 X 的值,称为浮点数

因此浮点数也是用定点数表示的
因此数值的表示问题就是定点数的表示问题
定点数的表示
定点数的进制、小数点位置都已确定,还需要确定的是编码方式
原码:最高位为符号位,0表示正数,1表示负数,其余位表示数值
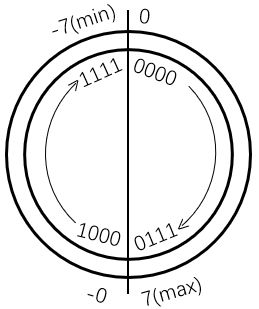
看起来像把整个编码空间平分,正负数的映射各占一半
原码的问题:
- 0的表示不唯一,0:0000 000;-0:1000 0000;
- 无法用加法实现减法,需要时时考虑符号
- 要额外考虑符号位,不利于硬件设计
- 特别当 a < b 时,实现 a - b 比较困难
从50年代开始,整数都采用补码进行表示(浮点数的尾数用原码定点小数表示)
移码(增码):将每一个数值加上一个偏置常数(Excess/bias),或者说二进制表示的数减去偏置常数
通常编码位数为 n 时,bias 取 2n-1 或 2n-1-1(IEEE 754)
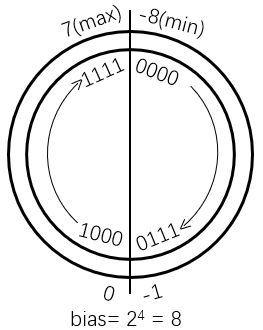
即,将所能表示的数从小到大依次映射到编码空间
移码的特性:当 bias 取 2n-1 时,移码和补码只有第一位不同
移码用来表示浮点数的阶:便于浮点数加减运算时的对阶操作(比较大小),
例:1.01×2-1 + 1.11×23,运算时,要将较小的 1.01×2-1 转换为 23 的表示
此处的阶使用移码进行存储,通过比较 0111(-1) < 1011(3),得到指数的大小关系
补码:补码的概念基于模运算,在模运算系统中,mod 模数 的结果相同的数是等价的(同余的数等价)
负数的补码等于模数加上该数,或者将数值位按位取反再加1
正数的补码等于该数本身
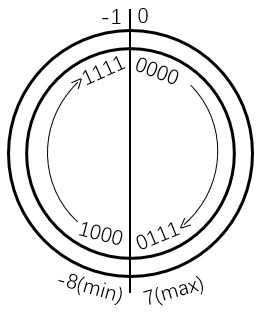
即编码空间分为两部分,非负数与负数首尾相接,且 min = -max-1,因为负数部分不再表示0
减去一个数相当于加上这个数的相反数的补码
例:7 - 7 = 7 + (-7) = 0111 + 1001 = 0000
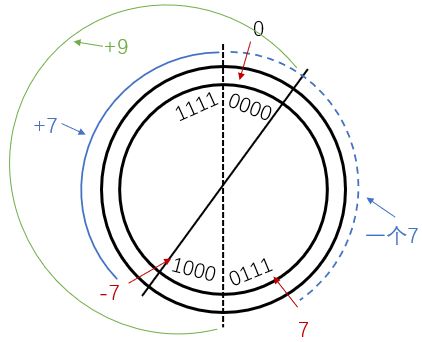
或者说逆时针减7相当于顺时针加上-7对 24 的补码9
补码的便利:统一了加操作与减操作
变形补码:使用两位作为符号位,后一个符号位可表示数据
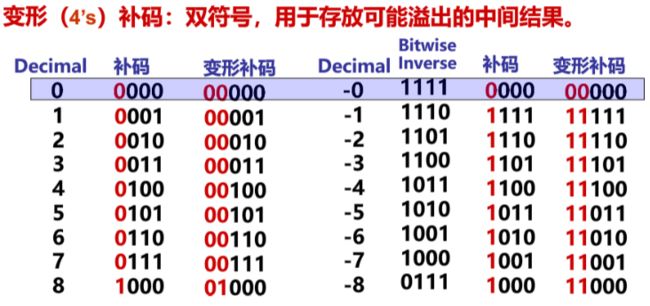
溢出判断:
单符号位:0表示整数,1表示负数
最高有效位有进位而符号位无进位,上溢
最高有效位无进位而符号位有进位,下溢
双符号位 / 模4补码 / 变形补码:00 表示正数,11表示负数
01上溢,10下溢
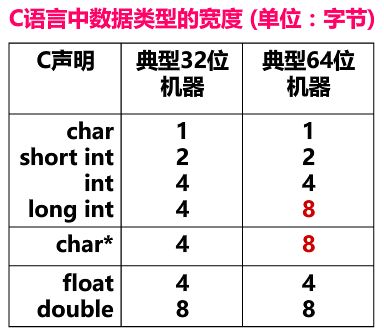
C语言支持的基本数据类型
(无符号)整数和浮点数,无符号整数没有符号位,所有位都用来表示数据
int x = -1;
unsigned u = 2147483648;
printf("x=%u=%d\n",x,x);
printf("u=%u=%d",u,u);
结果为
x=4294967295=-1
u=2147483648=-2147483648
由机器码解释,x = 0xFFFF,u = 0x8000
因此 x 作无符号数解释时,x = 232-1;u 作有符号数解释时,为 -231
编译器处理常量时的默认类型
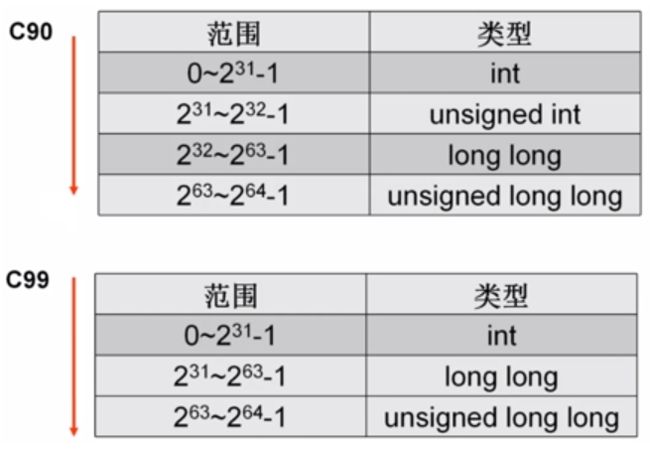
Integer Promotion:当表达式中存在无符号数与有符号数的运算时,有符号数按无符号数处理
因此,ISO C90标准的某些情况下,表达式 -2147483648 < 2147483647 的结果为0
因为 -2147483648 被当做 -2147483648u 、-(unsigned)2147483648 处理,且对无符号数取负是无效的

MSVC的报错信息(GCC可以通过):
![]()
最终两边按照无符号数比较大小,结果为0
但如果写为 -2147483647-1 < 2147483647,等式左边就会正常解析为 int 型,得到结果为1
浮点数的表示及范围
前面说过,实数 X 表示为类似科学计数法的形式 (-1)S× M × 2E,确定S、M 和 E 即可表示一个实数
以 32 位浮点数为例,

第 0 位符号位;1~8 位表示阶码E(移码存储,偏置常数128);9~31 位为 23 位的二进制原码小数 xxxx
约定尾数 M 的整数位始终为1(为 0 则 E 的变化范围变小了),完整的尾数为 1.xxxx,这种尾数的整数部分始终为1的形式称为规格化形式(Normalized form)
这样,最大正数 = 1.1111 1111…111 × 2127 = (1-2-24) × 2128
最小正数 = 1.1111 1111…111 × 2-128 = (1-2-24) × 2-129
由于表示正负数的 M 是相同的,符号仅由 S 位控制,所以正负数的表示范围是关于0对称的

下溢附近的值可近似表示为0
机器0:尾数 M 全零
浮点数表示范围比定点数大,但是编码个数没有变多,因此数之间更稀疏、且不均匀、不准确
IEEE754
早期计算机有各自定义的浮点数格式,因此在不同计算机之间进行程序移植时,需要考虑浮点数格式之间的转换
因此1985年IEEE制定了浮点数标准IEEE 754,现在所有通用计算机都采用该标准表示浮点数
IEEE 754 中,阶码的全0和全1用来表示特殊值,且偏置常数选择 2阶码位数-1-1,
(若选择 2阶码位数-1,以32bit为例,阶数范围为-127~126,偏置常数-1后,阶数范围为-126~127,扩大了数的表示范围)
对于单精度浮点数(single)和双精度浮点数(double),bias分别为127,1023
single:1+8+23 = 32 bits double:1+11+52 = 64 bits
例:float型变量的机器数为 BEE00000H
1011 1110 1110 0(repeats 20) → 1 0111 1101 110(repeats 21) = -1.11×2125-127B = -111/24B = -7/16 = -0.4375
全0阶码、全1阶码表示的特殊值:
- 阶码全0,尾数全0,表示0,按符号位,分为+0、-0
- 阶码1~254,尾数任意,表示规格化数(E,[-126,127])
- 阶码全1,尾数全0,按符号位分为±∞
所以,浮点数除以0的结果是 ±∞,而不会出现异常 - 阶码全1,尾数非0,表示NaN,非数值
- 阶码全0,尾数非0,表示非规格化数,(-1)S × 0.xxxx × 2-126,填补0与±2-126间的空白
非规格化非在,现在整数位约定为0了

很容易看出,规格化数是不均匀的,阶码全0,尾数非0表示的非规格化数是均匀的
有些十进制数是无法精确地按照这种编码方式表示的,比如61.420001,此时计算机中存储的是最接近的可表示数
非数值数据的编码表示
逻辑数据:真/假恰好映射为1/0,按照逻辑运算规则运算
西文字符:字符数量较少,常用编码为ASCII码,1个字节,略
汉字及国际字符的编码表示:数量巨大,总数超过六万
- 输入码:对汉字用相应按键进行编码表示,用于输入,比如拼音码
- 内码:用于在系统中进行存储、查找、传送等处理的01序列
- 字模点阵或轮廓描述:描述汉字字模点阵或轮廓,用于显示/打印
西文字符没有输入码,内码即ASCII码,同样有用于显示/打印的字模点阵或轮廓描述 - GB2312-80字符集
- 包括字母,数字和各种符号,包括英文、俄文、日文平假名与片假名、罗马字母,汉语拼音等共678个
- 一级常用汉字,共3755个,按汉语拼音排列
- 二级常用汉字,共3008个,较少使用,按偏旁部首排列
- 汉字的区位码
- GB2312-80编码表由94行、94列组成,行号为区号,列号为位号,各占7位
- 区位号确定汉字在码表中的位置,共14位,区号在左,位号在右
- 汉字的国标码
- 每个汉字的区号位号各自加上32(20H),及该字的国标码
- 为方便处理,在区号,位号前各加一位0,构成一个字节
多媒体信息的表示
图形、图像、音频、视频等信息在机器内部也用0和1表示
只不过多媒体信息用复杂的数据结构描述或编码方式编码,本质上都是01序列
数据宽度和存储容量单位
数据的基本宽度
比特(bit,位):是计算机中处理、存储、传输信息的最小单位
字节(byte):二进制信息最基本的计量单位;
现代计算机中,存储器按字节编址;
字节是最小的可寻址单位;
若以字节为一个排列单位,LSB标识最低有效字节,MSB标识最高有效字节
字(word):表示被处理信息的单位,用来度量数据类型的宽度;
两个字称为双字(DWORD),同理还有QWORD
字长:字的位数称为字长,指数据通路的宽度;
字长等于CPU内部总线宽度、运算器的位数、通用寄存器的宽度,即计算机能直接处理的二进制数据的位数;
字长概念还可以细分为:
- 机器字长:即一般提到的字长概念,也是CPU单次可以处理的最大数据长度
- 指令字长:一个指令字中包含的二进制代码的位数
- 存储字长:一个存储单元存储二进制代码的长度
字和字长的宽度可以一样,也可以不同
如x86体系结构,字的宽度都是16位,而IA-32(Intel Architecture 32-bit)的字长为32位;AMD64架构的字长为64位;
对于MIPS 32体系结构,字与字长都是32位;
数据通路:指CPU内部数据流经的路径及路径上的部件,主要是CPU内部进行数据运算、存储和传输的部件,这些部件的宽度基本上要一致,才能相互匹配;
数据量的度量单位
经常使用的容量单位有B(Byte)、KB、MB、GB、TB,其间换算大小为1024
通信中的带宽使用的单位有:
千比特/秒 kb/s、兆比特/秒 Mb/s、千兆比特/秒 Gb/s、兆兆比特/秒 Tb/s,其间换算大小为1000
同理,千字节/秒 KBps,兆字节/秒 MBps
数据类型宽度
- 不同机器上同一数据类型的宽度可能不同
- 为不同数据类型分配的字节数随ISA(指令体系结构)、机器字长和编译器的不同而不同
数据的存储和排列顺序
有 int a = 10,a 在计算机中的表示是 0x 00 00 00 0A,占四个字节
假设 &a 得到结果0x00004725,
这个地址是变量 a 所占空间的起始位置,及 a 存放在 0x00004725 ~ 0x00004728,
那么从 0x00004725 ~ 0x00004728,数据存放的顺序是00 00 00 0A 还是 0A 00 00 00呢?
这两种顺序就是以下两种存储方式
| 数据 | 00 | 00 | 00 | 0A |
|---|---|---|---|---|
| 大端方式 | 4725 | 4726 | 4727 | 4728 |
| 小端方式 | 4728 | 4727 | 4726 | 4725 |
| 有效字节 | MSB (最高有效字节) |
LSB (最低有效字节) |
小端:低位放在低字节 (x86架构)
大端:低位放在高字节 (MIPS、IBM 360/370等)
C语言 union 的存放顺序是所有成员从低地址开始,利用该特性来检测CPU的大/小端方式
int main(){
union{
int a;
char b;
}num;
num.a = 0x12345678;
if(num.b==0x78){
printf("小端 num.b=0x%x",num.b);
}else{
printf("大端 num.b=0x%x",num.b);
}
return 0;
}
下表中地址 高 → 低
| 变量a | 12 | 34 | 56 | 78 |
|---|---|---|---|---|
| 大端方式 | 变量b | |||
| 小端方式 | 变量b |
大/小端存储方式举例
假设某机器中,某指令的地址为1000
该指令的汇编形式为 mov AX,0x12345(BX) ,若操作码mov为40H,
寄存器 AX 和 BX 的编号分别为0001B和0010B,立即数占32位
(立即寻址方式指令中给出的数称为立即数)
则按大/小端存储顺序,有下面两种情况
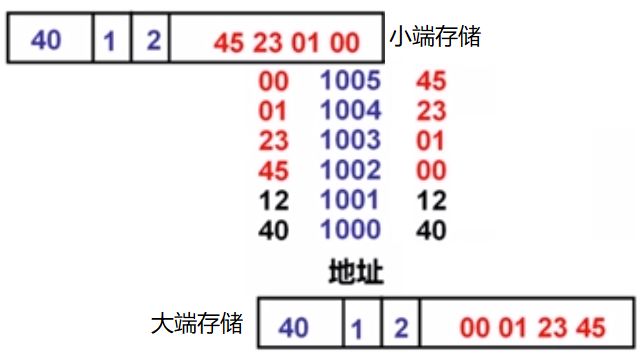
也就是说,只需要考虑指令中立即数的顺序
并且可以看出,在内存中,一行指令的存储是由指令地址开始按字节向高地址存放的
因此,在存放方式不同的机器间进行程序移植或者数据通信时,要注意顺序的转换
比如音、视频和图像等文件格式或处理程序都涉及到字节顺序问题,其中常见的格式如下:
小端存储:GIF,PC Paintbrush,Microsoft RTF,
大端存储:Adobe Photoshop,JPEG,Mac Paint,
2019/8/2
2020/3/5 修正规格化数的定义