计算机系统基础

C 语言相关内容省略，复习自用，仅供参考~

概述

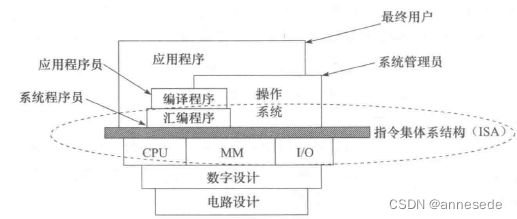
冯·诺伊曼结构

存储程序工作方式：将事先编好的程序和原始数据送入主存后才能执行程序，程序被启动执行后，计算机能在不需要操作人员干预下自动完成逐条指令取出和执行的任务。

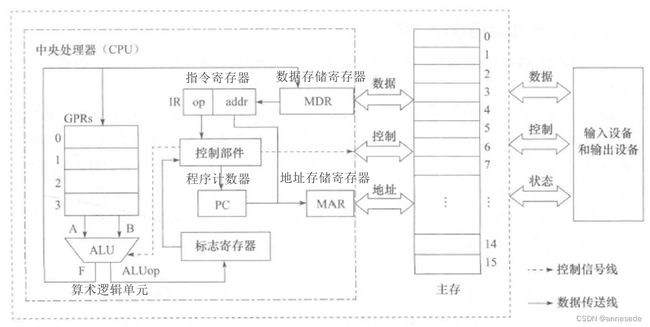
程序执行过程：主存取指令 $\to$ 指令译码 $\to$ PC 自增 $\to$ 取操作数并执行 $\to$ 结果送往主存或寄存器。

层次结构

性能评价

单位时间完成的工作量：吞吐率，带宽；作业提交开始到完成所需的时间：响应时间，执行时间，等待时间或时延。

用户 CPU 时间 $=$ 平均时钟周期数 $\times$ 时钟周期 $=$ 平均指令条数 $\times$ CPI $\times$ 时钟周期.
时钟周期（ns） $=1/$ 时钟频率（GHz）；$1$ GHz = $10^3$ MHz $=10^9$ Hz；$1$ s = $10^9$ ns.
CPI（执行一条指令所用的时钟周期） $=$ 平均时钟周期数 $÷$ 平均指令条数.
MIPS（平均每秒执行百万条指令数）$=1/$ 时钟周期（ns） $÷$ CPI $\times 10^{-6}$.

CPI 越低，时钟频率越高（即时钟周期越低）时，用户 CPU 时间越低（即CPU执行速度越快）。
峰值 MIPS 在 CPI 最低处。

整体改进后速度提升倍数 $=1/($ 改进部分时间比例 $/$ 改进部分速度提升倍数 $+$ 未改进部分时间比例 $)$.

数据

整数

进制转换：${b_n...b_0.b_{-1}...b_{-m}}_{(R)}={{\sum }_{i=-m}^n{b}_n{R}^n}_{(10)},m,n>0$.
2 进制 $\iff$ 16 进制：4 位一组。
小端存储：$A_1{A}_2|B_1{B}_2|C_1{C}_2|D_1{D}_2\to {D_1{D}_2{C}_1{C}_2{B}_1{B}_2{A}_1{A}_2}_{(16)}$.
字长：ALU 内部的数据宽度。
补码：正数符号位为 0，数值为自身；负数符号位为1，数值为按位取反后末位加 1。
求反：$-y=(\sim y)+1$，其中 $\sim$ 为按位取反。

加法器标志寄存器	ZF 零标志	OF 溢出标志	SF 符号标志	CF 进/错位标志
0	结果不为 0	结果未溢出（有符号）	结果为正	结果最高位发生进/错位；结果未溢出（无符号）
1	结果为 0	结果发生溢出（有符号）	结果为负	结果最高位无进/错位；结果发生溢出（无符号）

减法时，$x-y=x+((\sim y)+1)$ 中加法进位记为 $C$，则 $CF=!C$，其中 $!$ 为逻辑非。

异号相加，同号相减时，永远不会溢出。
正溢出：正数 $+$ 正数 $\to$ 负数，即正数 $-$ 负数 $\to$ 负数。
负溢出：负数 $+$ 负数 $\to$ 正数，即负数 $-$ 正数 $\to$ 正数。

浮点数（IEEE 754）

单精度值类型	符号（1位）	阶码（8位，偏置127）	尾数（23位）	值
规格化非零数	0 或 1	$0<e<255$	任意	$(-1{)}^s\times 2^{e-127}\times (1.f)$
正零	0	0	0	$+0$
负零	1	0	0	$-0$
正无穷大	0	全 1，即 255${}_{(10)}$	0	$+\infty$
负无穷大	1	全 1	0	$-\infty$
非规划化数	0 或 1	0	非 0	下溢，$(-1{)}^s\times 2^{-126}\times (0.f)$
非数	0 或 1	全 1	非 0	$NaN$

• 浮点数加减法
  对阶：小阶向大阶对齐，隐藏位还原到尾数。
  尾数加减：定点原码加减，注意符号。
  规格化：右规，尾数右移，阶码加 1；左规，尾数左移，阶码逐次减 1。
  尾数舍入：保护位 $+$ 舍入位 $+$ 粘位；就近舍入（0 舍 1 入），正向舍入，负向舍入，向 0 舍入。
  溢出判断：右规时会发生阶码上溢；左规时会变为非规格化数。

汇编（IA-32）

基础

• AT&T 格式
  指令形式：“op src,dst”，即 dst $\leftarrow$ dst op src.
  长度后缀：b $\to$ 8bit；w $\to$ 16bit；l $\to$ 32bit；q $\to$ 64bit.
  数字：“$number”.
  寄存器操作数：“%register”.
  存储器操作数（寻址方式）：“offset ( %base, %index, scale )”，即 %base $+$ %index $\times$ scale $+$ offset.
  指令类型：传送（数据传送/地址传送/标志传送/IO）；定点算术运算（加减乘除/自增自减/取负/比较）；按位运算（逻辑/移位）；控制转移（无条件转移/条件转移/条件设置/条件传送/调用返回/内中断）。
• IA-32 寄存器
  通用寄存器（32bit）：EAX 累加器，EBX 基址寄存器，ECX 计数寄存器，EDX 数据寄存器，ESP 栈指针寄存器，EBP 基址指针寄存器，ESI 源变址寄存器，EDI 目标变址寄存器。
  专用寄存器（32bit）：EIP 指针指令寄存器，EFLAGS 标志寄存器。
  段寄存器（16bit）：CS 代码段，SS 堆栈段，DS 数据段，ES FS GS 附加段。

C语言逆向

• 栈帧：每个未运行完的函数对应一个栈帧，保存了栈底（EBP）旧值、（被）调用者保存寄存器、传入参数、返回地址、局部变量。
  • 准备：形成新栈底（push, mov）；生成栈帧（sub 或 and）；保存现场（push）。
  • 过程：分配局部变量（auto）；处理具体逻辑；发生函数调用时（准备参数，call）；EAX 准备返回值。
  • 结束：出栈/销毁（leave 或 pop）；取返回地址返回（ret）。

Intel i386 System V ABI：EAX ECX EDX 为调用者保存寄存器；EBX ESI EDI 为被调用者保存寄存器。

• 地址传入：保存地址，再由地址传值。
• 选择结构 switch 语句：分段比较跳转实现；跳转表实现（生成索引数组）。
• 循环结构 for 语句：计数寄存器增/减步长，比较跳转实现。
• 连续内存（数组、字符串、结构体、联合体）：首地址确定。

// 内存对齐，对齐到 4 字节时
// 即 #pragma pack(4)
#include 
int main() {
    typedef struct {
        char sch1;
        char sch2;
        int si;
        short ss;
        double sd;
    } Align;
 
    char ch;
    int i;
    short s;
    double d;

    printf("%llu\n", sizeof(Align));
    printf("%llu\n", sizeof(ch) + sizeof(ch) + sizeof(i) + sizeof(s) + sizeof(d));
    return 0;
}

链接

ELF 文件格式：ELF 头 $+$ .text 节（目标代码）$+$ .rodata 节（只读数据）$+$ .data 节（已初始化全局变量）$+$ .bss 节（未初始化全局变量，占位符）$+$ .symtab 符号表（函数名和非局部变量名）$+$.rel.text 节（重定位）$+$ .rel.data 节（重定位）$+$ .debug 节（调试符号表） $+$ .line 节（-g 选项）$+$ .strtab 节（符号及节名）$+$ 节头表。
可读写数据段： .data 节（已初始化全局变量）$+$ .bss 节（未初始化全局变量，占位符）。

符号分类：全局 （非 static）；外部（extern）；本地（static）。
符号解析：强符号为函数名和已初始化全局变量名；弱符号为未初始化全局变量名；本地符号无强弱。
强符号只能定义一次；同时有强弱符号，符号类型以强符号为准，弱符号指向同一处地址；多个弱符号，任选其一。

例题

• 有符号整数表示（字长 16bit）
  0F 80 $\to$ 1000 0000 0000 1111 (补) $\to$ -32753${}_{(10)}$.
• 有符号整数减法（字长 8bit）
  A3H - 3AH $\to$ 1010 0011 (补) $-$ 0011 1010 (补) $=$ 1010 0011 (补) + 1100 0110 (补) $=$ 0110 1001 (补) $\to$ 69H; 标志 CF $=$ 0, OF $=1$, SF $=$ 0, ZF $=$ 0; 负溢.
• 单精度浮点数表示（大端）
  3FB00000H $\to$ 1.011B $\to$ 1.375 ${}_{(10)}$.
  C2FA4000H $\to -$ 1.111101001B $\to$ -125.125 ${}_{(10)}$.
• 单精度浮点数加法（大端）
  3FB00000H $+$ C2FA4000H $\to$ 对阶 0.00000101100 ${}_{(2)}+-$ 1.111101001 ${}_{(2)}$; 阶码 10000101 ${}_{(2)}\to$ 尾数加减 $-$ 1.11101111000 ${}_{(2)}\to$ 规格化 1 $|$ 1000 0101 $|$ 1110 1111 0000 0000 0000 000 $\to$ 尾数舍入(无) $\to$ C2F78000H.
• 链接（gcc -m32）

// main.c
#include 
int d = 100;
int x = 200;
int y = 300;
void p1(void);

int main() {
  y = 0;
  p1();
  printf("d=%d, x=%d, y=%d\n", d, x, y);
  return 0;
}

// p1.c
double d;
short y;
void p1(void) {
  d = 1.0;
  y = -100;
}

gcc -m32 -o linktest main.c p1.c
./linktest
>>> d=0, x=1072693248, y = 65436

$d=$ 1.0 (double, 64 bit) $\to$ 00 00 00 00 $|$ 00 00 F0 3F (小端)$\to x=$ 3FF00000H (大端), $d=$ 0 $\to x=$ 1072693248, $d=$ 0.
$y=$ -100 (short, 16bit)$\to$ 11111111 00110110 (补) $\to$ 10 01 11 00 11 11 11 11 $|$ 00 00 … (小端) $\to$ 65436${}_{(10)}$.