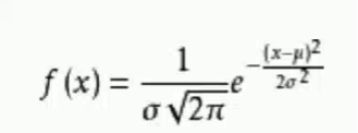《机器学习笔记（三）：多元线性回归与正态分布最大似然估计》

回归问题普遍讨论的是多元线性回归，考虑多个特征可以得到更精确的模型，这其中涉及中心极限定理，正态分布，概率密度函数和最大似然估计。

(一)背景——多元线性回归

1.概念

本质上就是算法（公式）变换为了多元一次方程组
y = F(x) = w1x1 + w2x2 + w3x3 + … + wnxn + w0*x0
W = （w0,w1…,wn）T
X = （x0,x1…,xn）T
这里W是n行的列向量，X也是n行的列向量

故也可以写为

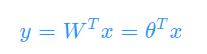
这里的W代表着权重（weight），举个例子
好瓜 = 0.5色泽 + 0.2根蒂 + 0.3敲声
在这诸多因素中，各个因素的系数代表权重，显然色泽在判断瓜的好坏这个模型中是更加重要的因素。

上述y是样本的预测值，若Y代表样本的真实值，error为误差

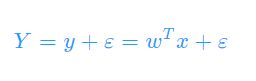
2.多元线性回归的流程*

假设有m个样本，每个真实样本与预测值都存在误差error，我们已知的数据集DataSet中有m*n的矩阵X和列向量真实值Y。

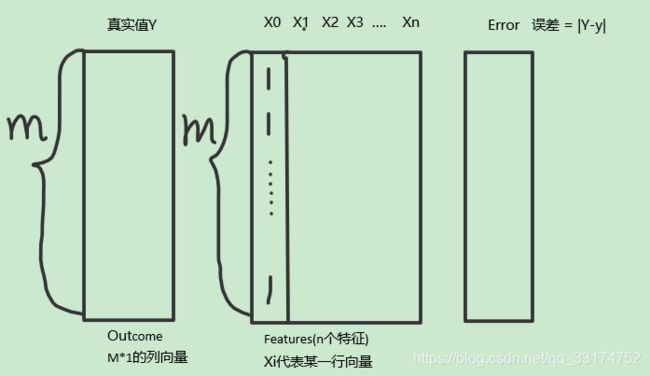
给出一组X矩阵和一列真实值Y，可以求解出
（w0，w1，…，wn）各权重，即求解出模型，当有新的X输入时，带入方程内可求得预测值y。
而 |Y-y| 就是误差error，这是个及其重要的概念。

联系上篇讲到的最小二乘法，就是要拿到所有样本的误差error，再代入损失函数求解，误差最小的时刻就是最优解模型。

求模型即求参数，那么，具体如何求参数呢？？？引入 “最大似然估计”概念

（二）最大似然估计

1.概念

最大似然估计是一种统计方法，用来求一个样本集（DataSet）的相关概率密度函数的参数。
当确定一个DataSet的正态分布时，即可对应一个正态分布的概率密度函数的Fuction。

2.反向求解

最大似然估计求参数的前提是该数据集符合某个正态分布。
当我们不确定这个DataSet符合何种正态分布，就可以用已知的DataSet去尝试，看它最符合哪一种正态分布，哪个正态分布所对应的概率密度最大，即这个数据集最匹配哪个正态分布。

3.概率密度函数

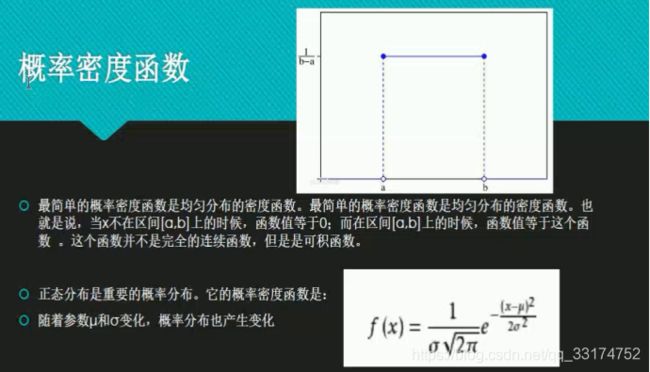
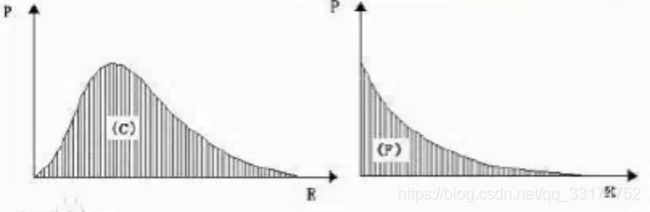
这里要理解一下，概率密度函数求出的并不是概率，而是概率密度。上面两张图，均是概率密度函数，其阴影部分面积的值是概率。求概率最大的情况，即求概率密度最大的情况，这个思想会在后面公式推导中有重要应用。

（三）中心极限定理

中心极限定理是概率论中讨论随机变量序列部分与分布渐进于正态分布的一类定理，这组定理是数理统计学和误差分析的理论基础，指出了大量随机变量累计分布函数逐点收敛到正态分布的积累分布函数的条件。

一定要假设是随机变量，只有随机变量才会服从正态分布

所以要假设数据集中每行X之间都是相互独立的，即符合中心才极限定理，才能去找这个DataSet对应的正态分布，于是能利用最大似然估计去解出这个正态分布对应的概率密度函数的参数。

Exp.举个例子，如下图即为德国足球运动员身高符合的正态分布的模型，大部分德国足球运动员身高都回归到1.8m左右，较矮的（1.6m）和较高的（2m）都比较少。

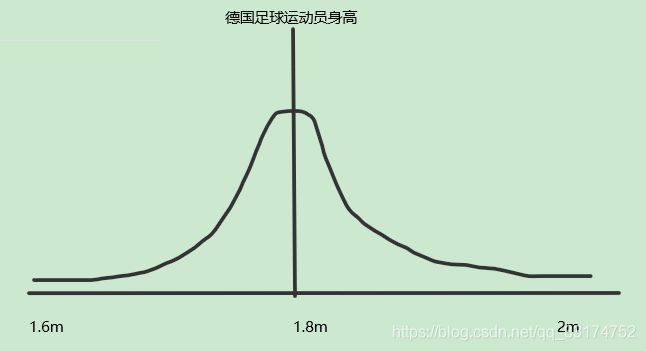
做线性回归用”试“的方法，通常要迭代找到数据集对应最合适的正态分布。

联系最小二乘法，

设中心点为样本预测，”好“的模型就是指样本真实值要”回归“到预测值附近。

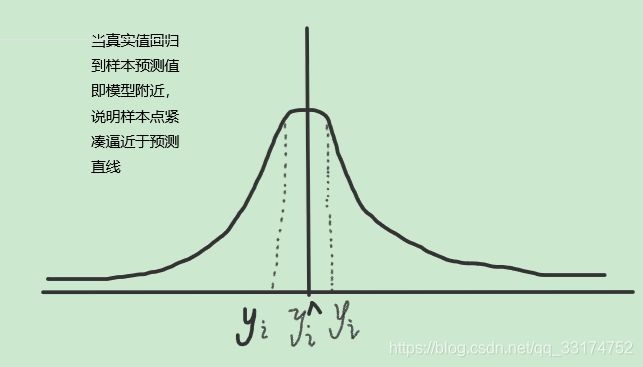
/********我是分割线************/

好啦，对于定理基本理解先到这里，接下来我们讨论如何使用概率密度函数来推导最小二乘法损失函数。

/********我是分割线************/

（四）**公式推导

1.将误差ERROR带入概率密度函数

A：
正态分布是重要的概率分布，其概率密度函数是

μ和σ可以唯一决定一个正态分布，x由数据集里面给出

B：
下式yi表示样本真实值，error代表样本点与模型的误差，中间项为预测值，后面需要用到此式将error替换为其他项。

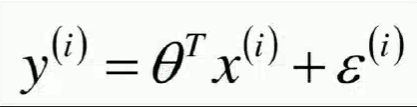
C：
***在机器学习中，我们把误差error看作是随机变量，即正态分布中真实值Y到预测值中间轴y的距离，即（x-μ）。将公式中的误差error = （x-u）带入概率密度函数，得到下式。

再将误差error替换为真实值和预测值，即x，y和theta

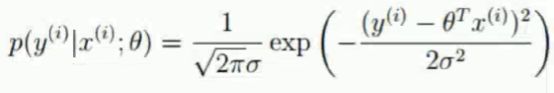
我是分割线

上式含义是m个样本中的一条数据的概率密度，也称一个似然。当我们把一组数据集DataSet所有行都带入一个正态分布中，得到的总概率最大，即这个数据集与这个正态分布最吻合。

前提：AB两个时间相互独立。联合概率公式：P（AB） = P(A)P(B)

首先假设各行数据均为随机变量，我们要做的就是把一组数据集DataSet所有行的似然都相乘得到总似然，在总似然最大时，就得到了该数据集最吻合的正态分布模型最优解

这里我们其实还做了一个等价，我们需要的是概率最大的情况，之前有提到，就等价于求概率密度最大的时刻，因为概率是概率密度函数的面积，需要求积分，不好求，所以引入这个等价。

我是分割线

2.最大总似然估计

A：
将单条样本似然相乘得到总似然，L（θ）中的L就代表着likelyhood，即似然。

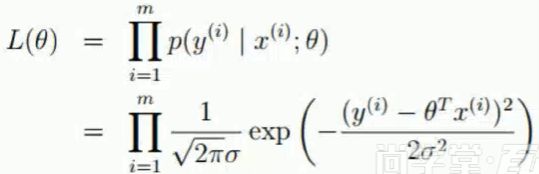
B：
我们的目的是要找到最大总似然，可上式是m个式子连乘，不易找其最大值，要将相乘变成相加，想到用对数处理：
L（θ）取对数得到l（θ），
累乘号变为累加号，
再将exp前面的系数分离，最后得到两项，
前面一项不含x，y，θ，只含σ和m
后面一项含x，y，θ，σ

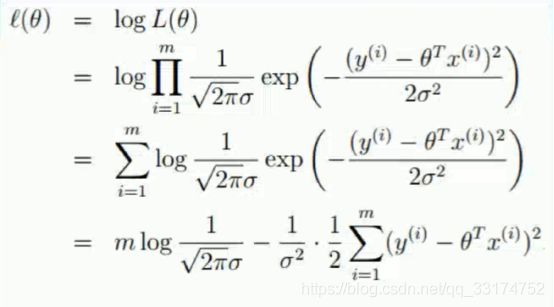
C：
显然，要求上式的最大值，即求下式J（θ）的最小值，hθ（xi）就代表了模型预测值（θ）Txi。
至此，把求数据集最吻合某个正态分布模型的参数转化为求J（θ）的最小时的情况

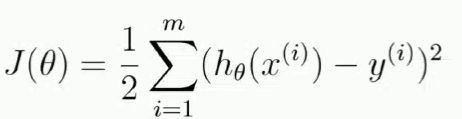
总结

欸？？大家有没有一些眼熟呢，J（θ）是不是和最小二乘法的目标函数非常之相像呢！！！

答案是肯定的，嗯，还有最小二乘法公式中误差的绝对值为何要加平方也算推导出来了。

至此我们已经根据公式推导出了最小二乘法的损失函数了，当损失函数最小时，我们就能得到该数据集最吻合的正态分布对应的概率分布函数的总似然最大的情况，也就是我们想要的最优解。然而，我们目前的方法只能迭代的去尝试各种不同的正态分布去选择最优解，有没有可以不用迭代，直接根据已知条件推出最优解的方法呢？

有，那就是根据损失函数直接推导出解析解。

如何推导出解析解以及其代码实现和对于梯度下降法的初步应用会在下一篇《机器学习笔记（四）：多元线性回归解析解推导及其代码实现与梯度下降法初步》中讨论。

BTW，在杭州过年冷的我到怀疑人生0.0