线性回归 最大似然估计及二乘法
作者:知乎用户
链接:https://www.zhihu.com/question/20447622/answer/23848605
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
最大似然估计:现在已经拿到了很多个样本(你的数据集中所有因变量),这些样本值已经实现,最大似然估计就是去找到那个(组)参数估计值,使得前面已经实现的样本值发生概率最大。因为你手头上的样本已经实现了,其发生概率最大才符合逻辑。这时是求样本所有观测的联合概率最大化,是个连乘积,只要取对数,就变成了线性加总。此时通过对参数求导数,并令一阶导数为零,就可以通过解方程(组),得到最大似然估计值。
最小二乘:找到一个(组)估计值,使得实际值与估计值的距离最小。本来用两者差的绝对值汇总并使之最小是最理想的,但绝对值在数学上求最小值比较麻烦,因而替代做法是,找一个(组)估计值,使得实际值与估计值之差的平方加总之后的值最小,称为最小二乘。“二乘”的英文为least square,其实英文的字面意思是“平方最小”。这时,将这个差的平方的和式对参数求导数,并取一阶导数为零,就是OLSE。
发布于 2014-03-27
司马懿
经济学、博弈论 话题的优秀回答者
谢邀,这个问题下的答案很多是直接从机器学习领域过来回答的,很有启发性,让我了解了在别的领域是如何理解这两种方法的。论及本质,其实两者只是用不同的度量空间来进行的投影,如同
@颢卿
的答案所提到的那样,OLS的度量是L2 norm distance,而极大似然的度量是Kullback-Leibler divergence.
不过这种高度抽象的统一框架,主要功能就是让人听起来很优雅很爽,满足了人对形式美的追求,缺点也很明显:
- 不在概率论方面下一些功夫不太能真正理解
- 无法直接拿过来应用
所以在大多数情况下,我们介绍这两种方法的时候,可能并不需要讲解这么抽象的东西。好,下面我们开始说人话^_^
设想一个例子,教育程度和工资之间的关系。我们观察到的数据无非就是一个教育程度,对应着一个工资。我们希望的自然是找到两者之间的规律:如果把教育程度的初中、高中、大学、研究生及博士定义为1234的话,我们希望找到类似于工资=1000 +2000x教育程度 的这种规律,其中1000和2000是我们需要从数据里面发现的,前者称之为底薪,后者称之为教育增量薪水。
如果我们就观察到两个数据,那解起来很简单,直接把两个数据带进去,二元一次方程组,就得到底薪和教育程度增量薪水之间的关系。这个在图上就体现为两点决定一条直线:
<img src="https://pic2.zhimg.com/50/v2-fae27da14b1efdeb88c87b1f40b0ff3d_hd.jpg" data-caption="" data-rawwidth="390" data-rawheight="233" class="content_image" width="390">
但是如果现在有三个数据,怎么办呢?如果这三个点不在一条线上,我们就需要作出取舍了,如果我们取任意两个点,那么就没有好好的利用第三个点带来的新信息,并且因为这三个点在数据中的地位相同,我们如何来断定应该选用哪两个点来作为我们的基准呢?这就都是问题了。这个时候我们最直观的想法就是『折衷』一下,在这三个数据,三条线中间取得某种平衡作为我们的最终结果,类似于图中的红线这样:
<img src="https://pic3.zhimg.com/50/v2-faae8e8d26791cc11245c91ee48eb5ce_hd.jpg" data-caption="" data-rawwidth="403" data-rawheight="233" class="content_image" width="403">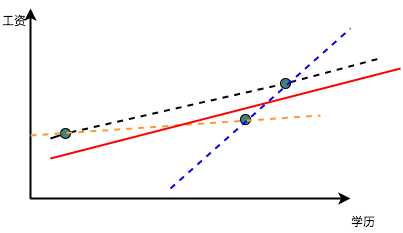
那怎么取平衡呢?那我们现在必须引入误差的存在,也就是我们要承认观测到的数据中有一些因素是不可知的,不能完全的被学历所解释。而这个不能解释的程度,自然就是每个点到红线在Y轴的距离。
但是我们尽管痛苦的承认了有不能解释的因素,但是我们依然想尽可能的让这种『不被解释』的程度最小,于是我们就想最小化这种不被解释的程度。因为点可能在线的上面或者下面,故而距离有正有负,取绝对值又太麻烦,于是我们就直接把每个距离都取一个平方变成正的,然后试图找出一个距离所有点的距离的平方最小的这条线,这就是最小二乘法了,简单粗暴而有效。
而极大似然则更加的有哲理一些。还用上面的例子,我们观察到了三个点,于是我们开始反思,为什么我们观察到的是这三个点而不是另外三个?大千世界,芸芸众生,这么多人都有不同的工资,不同的学历,但是偏偏这三个点让我给观察到了。这肯定说明了某种世界的真相。
什么世界的真相呢?因为我们观察到了这三个点,反过来说,冥冥之中注定了这三个点被我们观察到的概率可能是最大的。所以我们希望找到一个特定的底薪和教育增量薪水的组合,让我们观察到这三个点的概率最大,这个找的过程就是极大似然估计。
具体的做法很简单,因为底薪和教育增量薪水虽然我们不知道,但是它一定存在,所以是个固定的值,能够随机变动的就是我们观察不到的神秘误差,那么给定一组底薪和教育增量薪水,必然存在一个唯一的误差与之对应,共同组合成了我们看到的数据。比如说,我们观察到一个人是:
高中毕业(学历变量=2) 工资 4500,如果我们假定工资=1000 +2000x教育程度的话,那么理论上工资应该是5000,而我们观察到了4500,所以这个时候误差为500。而误差=500,根据我们假设的误差的概率函数,总是存在一个概率与之相对应的(这个概率的分布我们可以假设)。而极大似然估计,就是把我们观察到每个样本所对应的误差的概率乘到一起,然后试图调整参数以最大化这个概率的乘积。
其背后的直觉是:假想有一个神秘的超自然力量,他全知全能,自然也知道真实的数据背后的规律。他在你抽样之前先做了一次复杂的计算,把无数个可能的抽样中,最可能出现的那个抽样展示给你。于是你根据这个抽样,逆流而上,倒推出来了数据背后的真实规律。
总结一句话,最小二乘法的核心是权衡,因为你要在很多条线中间选择,选择出距离所有的点之和最短的;而极大似然的核心是自恋,要相信自己是天选之子,自己看到的,就是冥冥之中最接近真相的。^_^
编辑于 2017-11-07
渣君
债市小渣毛
说的通俗一点啊,最大似然估计,就是利用已知的样本结果,反推最有可能(最大概率)导致这样结果的参数值。
例如:一个麻袋里有白球与黑球,但是我不知道它们之间的比例,那我就有放回的抽取10次,结果我发现我抽到了8次黑球2次白球,我要求最有可能的黑白球之间的比例时,就采取最大似然估计法: 我假设我抽到黑球的概率为p,那得出8次黑球2次白球这个结果的概率为:
P(黑=8)=p^8*(1-p)^2,现在我想要得出p是多少啊,很简单,使得P(黑=8)最大的p就是我要求的结果,接下来求导的的过程就是求极值的过程啦。
可能你会有疑问,为什么要ln一下呢,这是因为ln把乘法变成加法了,且不会改变极值的位置(单调性保持一致嘛)这样求导会方便很多~
同样,这样一道题:设总体X 的概率密度为
已知 X1,X2..Xn是样本观测值,求θ的极大似然估计
这也一样啊,要得到 X1,X2..Xn这样一组样本观测值的概率是
P{x1=X1,x2=X2,...xn=Xn}=f(X1,θ)f(X2,θ)…f(Xn,θ)
然后我们就求使得P最大的θ就好啦,一样是求极值的过程,不再赘述。
发布于 2014-03-29
另外一篇http://www.cnblogs.com/monoSLAM/p/5257589.html