GAN的原理（二）

Basic Idea of GAN
我们开始讲一下真正的GAN的原理，前面都是概要性的叙述，接下来要讲GAN是怎么回事，
判别器与生成器之间他们互相对抗的结构他们是发生了什么样的事情，为什么可以产生真实的图像。

我们从极大似然估计开始
首先我们有一个真实图片集的分布Pdata(X),X就是个真实图片，把其所有的pixel串起来可以想象成一个向量，这个向量的几何的分布就是Pdata。我们需要生成一些也在这个分布内的图片，如果直接就是这个分布的话，应该很难做到吧。
如果我们要生成一张image,我们需要找一个distribution，这个分布是受控于一组parameter?。我们要找一个分布，这个分布就是?_? (?;?) ，其受到一组参数?所操控的，这个?决定了这个?_? (?;?) 长什么样子，
我们为什么要找一个PG与Pdata很像呢？？那是因为这个Pdata我们不太容易从它里面做sample，可以这么说这个Pdata是我们手上已经有的，他就代表我们手上的image，那你现在你要多sample一张Pdata，其实有点麻烦，必须从新画一张动漫图。?_? (?;?) 里的?受我们操控，现在我们有?_? (?;?) 我们想画多少张图就可以画多少张图。
?_? (?;?) 可以是高斯混合模型，那么?可以是每个高斯分布的平均值和方差。
我们就是要找到一个?让PG跟Pdata越接近越好。怎么做这件事情呢？如果是高斯混合模型的话，我们从Pdata里面去sample一堆的训练数据，比如sample出来x1,x2,xm，举例来说其分布就像右边的图像，接下来我们有办法去计算，给我们这些参数?,假设这些参数?是已经给定的，sample出Xi这些的几率，假设这些都是可以计算的。
接下来呢就可以定义一些东西就像likelihood，意思就是说给我们一个?我们就定义出PG，这个PG产生这一堆x1…xm，它的可能性有多大就是likelihood。
likelihood就写成了我们把sample出来的每一个Xi都去计算?_? (?;?) ，再乘起来就是我们的likelihood，
我们想要最大化这个似然，等价于让gen生成那些真实图片的概率最大，就变成了一个最大似然估计的问题了，给我们一组参数?我们可以计算likelihood，找一个参数?^∗ 可以让likelihood越大越好。
如果是高斯混合模型，那么你要找的平均值和方差，假设有三个mixture，找到的mean就是这三点找到的方差就是蓝色的圈圈这个样子。

这个极大似然我们可以对其做一下转换，我们可以把likelihood前面取一个log不会影响我们找出来的?，我们可以把log相乘变成相加然后取log，因为我们x1…xm都是从Pdata（x）中sample出来的n批data
我们从pdata的分布里面sample X。从这个X去计算产生的几率所产生的期望值，我们没有办法对?_(?~?_???? )做积分，接下来从每个Pdata中sample X，再从X中去计算这个log 几率这件事情，如果你把它取积分的话，我们要做的事情其实就是积分所有的x,然后呢算这个Pdata的X，再乘上log的?_? (?;?)，后面可以剪掉这一项，这一项只跟Pdata有关，跟?完全无关，所以剪掉这一项并不会影响你找出来的?，之所以剪掉这一项是为了我们要把极大似然这件事情化简成minmize KLdivergence的形式了。KLdivergence是描述两个概率分布之间的差异。
接下来我们把都是积分的部分放在一起，乘在log后面的东西也一样也都是Pdata，就可以将其提出来。
在maximum likelihood的事情就是要找到一个参数?，根据这个?所定义出来的PG，它和我们的Pdata的KLdivergence越接近越好。
PG到底是什么？PG就是高斯混合模型，是有限制的。它不能model所有的Pdata，事实上使用高斯混合模型去产生image，最早作出的图像都很模型，因为高斯混合模型没有真正的办法去逼近Pdata，不能去真正的模拟，所以会很模糊。
GAN的好处是我们可以由一个非常复杂的PG，非常一般化的PG。

如何拥有一个非常一般化的PG呢，就是把你的PG用一个NN来定义，也就是我们的?可以用一个神经网络参数来定义，假设这个神经网络的参数已给出，那个这个G就是一个function，input是一个向量Z，通常这个Z是低维的向量，Z这个向量丢到G里面它的output就是一张image。NN是怎么定义这个分布的呢？input这个Z是一个分布的话，那这个NN的output就可以把它看做是一个distribution。假设这个Z是从高斯分布里面sample出来的，把这个sample出来的Z通过G得到一组X，这个X就是另外一组distribution。，会不会产生的distribution很接近normal，这样就跟我们刚才说的跟高斯混合模型差不多。这个不用担心神经网络只要有非线性激活函数，就可以拟合任意的函数，那么分布也是一样的，所以可以用正太分布或者高斯分布取样去训练一个神经网络，学习到一个很复杂的分布。即使是input一个非常简单的分布，他也可以变得非常的复杂。
这个网络的distribution要是写成式子应该长什么样？？方程。。。
x出现的几率从网络取样X的几率，假设参数?已经给定了，+积分所有可能的z，每个Z出现的几率不一样，乘上Z的prior,每个Z通过functionG得到x，如果等于就是1不等于就是0，用I下标来表示，这样写没办法算likelihood，之前高斯混合模型给出X就可以轻易算出这个X出现的几率，但是我们使用NN，给一个X，即使知道这个prior的分布长什么样，但是这个G是个很复杂的function要求出X的几率变得很困难，就卡在这里了。gan最大的贡献就是解决了这个问题，在没有办法算likelihood的情况下我们应该如何调整生成器的参数?，让生成器的产生的分布接近data的分布呢。

我们假设有个GEN G，就是一个function，不是网络也没有关系，现在都用神经网络来表达，输入是Z,输出是X，我们要先定义好一个预先的分布，然后可以定义出一个PG，怎么算PG？？
GISC也是一个function，inputX, output是一个标量，这个判别器的左右是衡量PG与Pdata有多相近，现在有个G，我们不会算likelihood，我们不知道这个G所定义的PG与Pdata KLdivergence是多少，突然来了一个判别器，这个判别器会算PG与Pdata之间另外的divergence，怎么计算两个分布之间的divergence？就是让它解下面这个方程
先定义一个function先定义一个V(G,D)。这个function就是有一个gen一个disc会output一个数值，
要找到跟data分布最接近的?^∗ 其实就是下面这个式子找出来的，我们需要找一个?去max????，一个?需要minmize

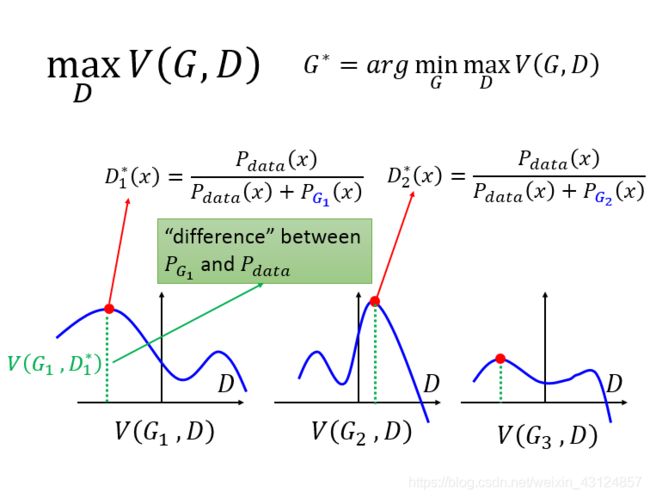
我们先看右上角画红线的地方，这个地方是说我们要找一个D,这个D可以maxmizeV（G,D）假设说现在的G只有三个选择，就是G1,G2，G3这个GEN是由network 的参数决定的，参数不同就不同的G
定住G1去改变D就会得到不同的数值，。。。。
如果G就是G1的话，那么maxV(G,D)就是这个红点的数值
接下来我们要minmize这个划红线的部分，划红线的部分受G1的影响，我们要minmize这个划红线的部分大家认为是G1,G2，G3？？解出来的就是G3。找到的是
先不要关V怎么来的，就写成这样，当我们把V写成这样的话，给定一个gen,maxV就是这个gen的PG跟data之间的某种divergence,差异。红点到X轴之间的高就是G1跟data之间的差距，G3与data之间的差距最小，所以G3就是我们要找的gen
接下来就要说为甚是这样子了。

第一个说明是事情是给定一个G的时候，假设我们已经定义好V了，到底哪个D* 可以让V最大，这个式子被maximizing，这个式子是假设我们从Pdata里去sample X出来放入这个D里面，这个D是个function，然后求出其log的期望值再加上从PG里面去sample X，再取log（1-D）的期望值。给定G就是给定了PG的分布，哪一个D可以让V值最大，就把它做展开，Pdata的几率乘上logD，加上积分PG的几率乘上LOG(1-D)。
积分里面的东西放一起我们就得到了中括号里面的东西。
假设D（x）可以是任何function，D(X)output可以是任何数值，在这个前提之下，我们应该怎么设置D可以让V最大，我们如何可以让中括号里面的值最大？？

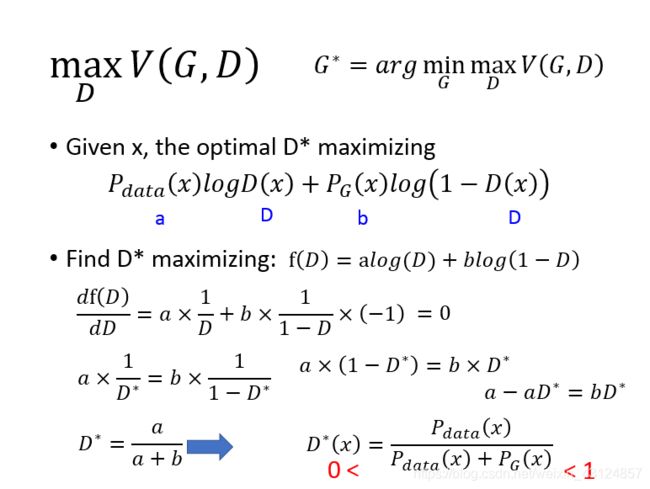
为了简化我们Pdata我们用a表示，logD（x）我们用D表示，PG我们用b表示。data分布是给定的，其是一个值，PG也是给定的。现在我们可以调动的就是D。
为了找到极值，我们先做微分，把这个式子对D做微分，极值令它等于0.。。。
最后最好的D的output这个值是介于0-1之间的，即使是神经网络我们可以加上sigmoid让其边到0-1之间。

给定了G后的哪一个D是最好的，当给定G1时候红点的D就是最好的值，就是?_1^∗ (?)产生的。
现在我们已经知道?_1^∗ (?)可以让值最大，接下来我们要求出这个高是多少，要求高我们要把?_1^∗ (?)带到V(G,D)function里面去，跟G1一起求出V(G,D)，这个值就是在衡量PG1与Pdata之间的某种divergence。

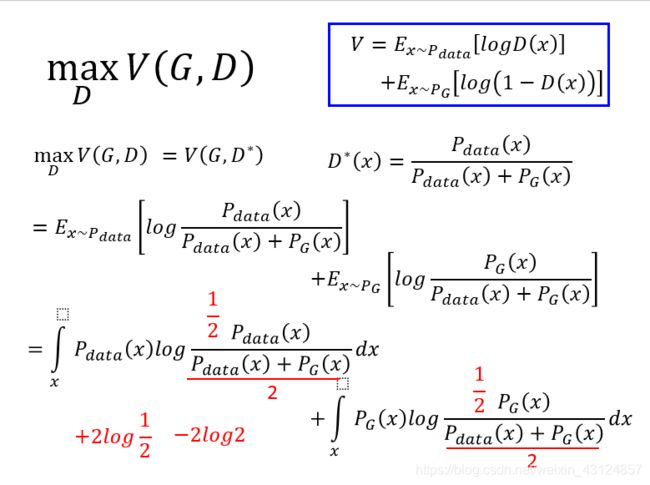
我们知道?^{∗，然后带到max┬?⁡?(?,?)，计算?(?,?}∗ )，G是给定的?^{∗会受到G的影响。反正关系就是这个式子?}∗ (?)=(?_???? (?))/(?_???? (?)+?_? (?) )。
怎么求V呢我们使用V的定义?=?_(?∼?_???? ) [????(?)]+?_(?∼?_? ) [???(1−?(?))]，把?^∗带到里就是?_(?∼?_???? ) [??? (?_???? (?))/(?_???? (?)+?_? (?) )]+?_(?∼?_? ) [??? (?_? (?))/(?_???? (?)+?_? (?) )]，
把求期望值改成积分，∫17_?▒〖?_???? (?)??? (?_???? (?))/(?_???? (?)+?_? (?) )〗 ??+∫17_?▒〖?_? (?)??? (?_? (?))/(?_???? (?)+?_? (?) )〗 ??。
接下来把分子分布上下都除以1/2，我们可以吧1/2这一项拿出来

第一项就Pdata与（Pdata和PG ）的平均的的KL divergence。第二项就是PG与（Pdata和PG ）的平均的的KL divergence。
我们知道KL是非对称的。但是这个divergence是对称的这个divergence叫做Jensen-Shannon divergence。

总结一下，我们有一个G一个D。定好了一个V的值function，是个data是有关系的。
我们要找一下?^∗，是??? min┬?⁡max┬?⁡?(?,?) 问题的解，找一个D让?(?,?)的值最大，跟JSD的大小是一致的，JSD的值最大为log2，最小为0。?(?,?)最大值就是0最小值就是−2log2
找一个G可以让max┬?⁡?(?,?)最小，?_? (?)=?_???? (?)情况下其值最小。接下来就是解min┬?⁡max┬?⁡?(?,?) 这个问题。

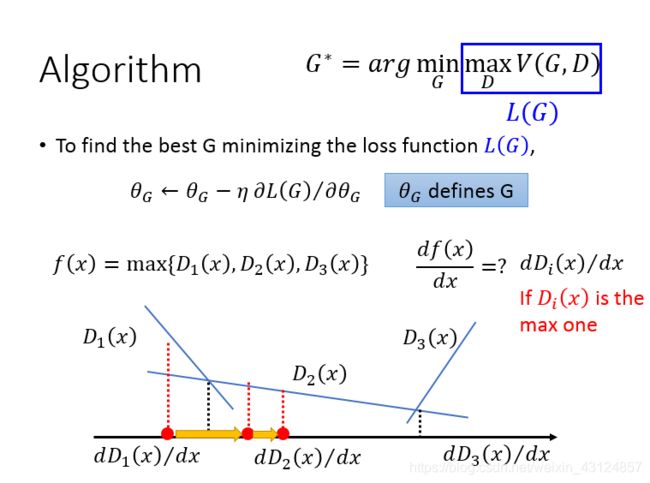
如何解？我们先把蓝色框里的东西写成L（G），蓝色框里的东西只跟G有关。找到最好的G就是需要minimizing loss function ?(?)
是?_?对??(?)的偏微分，去updata我们的参数

假设?(?)=max {?_1 (?),?_2 (?),?_3 (?)}对??(?)/?? 值是多少，?_1 (?)的值是那条直线。。。。微分值取决于X落在哪个区域就用哪个区域的D求最大值。

所以如何找个G能够minmaxV，有一个初始的G0，哪一个D可以让V最大。
接下来计算?_?对V 的点，updata我们的G 生成G1 ，

有个小小的问题就是给定一个G0把D0带到Vfunction里面，我们可以量出JS divergence.我们Updata G0,将G0变为G1,我们定住这个?_0^{∗的情况下，让V1∗≈?_1^∗ 很接近。所以不好更新?太多。如果updata跨步太大步会使损失函数不减反而增。}

本文的PPT是使用台湾大学李宏毅老师公开课的PPT。