钢管下料问题模型求解
文章目录
- 钢管下料问题模型求解
-
- 一、问题描述
- 二、问题分析
- 三、实验原理
- 四、运行结果
- 五、源代码
钢管下料问题模型求解
关键词:钢管下料
Python、Lingo
一、问题描述
某钢管零售商从钢管厂进货,将钢管按照顾客得要求切割后售出,从钢管厂进货时得到得原料钢管都是19m。
- 现有一客户需要
50根4m、20根6m和15根8m的钢管。问应如何下料最节省? - 零售商如果采用的不同切割模式太多,将会导致生产过程的复杂化,从而增加生产和管理成本,所以零售商规定采取的切割模式不超过
3种。此外,该客户除需要(1)中的三种钢管外,还需要10根5m的钢管,问应如何下料最节省?
二、问题分析
问题一:
①要使下料最节省,根据实际需要,可选择总余量最小和所用原料钢管根数最少作为目标。在余料没有什么用途的情况下通常选择所用总根数最少为目标。
②对于每种切割模式必须合理,即每根钢管剩余原料必须小于4m。
问题二:
①本题的目标为利润扣除废料之后净利润最大。废料分为两种,一种是余料,一种是不能匹配的罐底瓶盖、底。
②在该题中,易拉罐个数为整数,但是由于生产数目巨大,故可看作实数。
三、实验原理
问题一: 钢管的切割模式
用
python或枚举法列出所有合理的切割模式
| 4m钢管数 | 6m钢管数 | 8m钢管数 | 余料/m | |
|---|---|---|---|---|
| 模式一 | 4 | 0 | 0 | 3 |
| 模式二 | 3 | 1 | 0 | 1 |
| 模式三 | 2 | 0 | 1 | 3 |
| 模式四 | 1 | 2 | 0 | 3 |
| 模式五 | 1 | 1 | 1 | 1 |
| 模式六 | 0 | 3 | 0 | 1 |
| 模式七 | 0 | 0 | 2 | 3 |
问题二: 钢管切割模式
用
python或枚举法列出所有合理的切割模式
四、运行结果
问题一:
python求解
fun: 25.0
message: ‘Optimization terminated successfully.’
nit: 4
slack: array([0., 0., 0.])
status: 0
success: True
x: array([ 5., 0., 5., 0., 0., 15., 0.])
问题二:
python求解
lingo求解
Local optimal solution found.
Objective value: 28.00000
Objective bound: 28.00000
Infeasibilities: 0.000000
Extended solver steps: 145
Total solver iterations: 9131
五、源代码
问题一:
python
# -*- coding: utf-8 -*-
from scipy import optimize as op
import numpy as np
b_list=[]
c_list=[]
for i in range(5):
for j in range(4):
for k in range(3):
if 16<=4*i+6*j+8*k<=19:
a_list = [] #存储一种情况
a_dict = {
} #存储一种情况的数据
a_dict["x"]=i
a_dict["y"]=j
a_dict["z"]=k
a_list.append(a_dict)
b_list.append(a_list)
f=np.array([1,1,1,1,1,1,1])
a=[];b=[];c=[]
for k1 in range(7):
a.append(b_list[k1][0]["x"])
for k2 in range(7):
b.append(b_list[k2][0]["y"])
for k3 in range(7):
c.append(b_list[k3][0]["z"])
a=np.asarray(a);b=np.asarray(b);c=np.asarray(c)
A=np.array([a,b,c])
b=np.array([50,20,15])
x=op.linprog(f,-A,-b)
print(x)
lingo
MODEL:
sets:
v1/1..7/:c,x;
v2/1..3/:b;
link(v2,v1):A;
endsets
data:
c=1,1,1,1,1,1,1;
A=4,3,2,1,1,0,0
0,1,0,2,1,3,0
0,0,1,0,1,0,2;
b=50,20,15;
enddata
min=@sum(v1(i):c(i)*x(i));
@for(v2(i):@sum(v1(j):A(i,j)*x(j))>b(i));
@for(v1(i):@gin(x(i)));
end
问题二:
python
# -*- coding: utf-8 -*-
#from scipy import optimize as op
import numpy as np
import cvxpy as cp
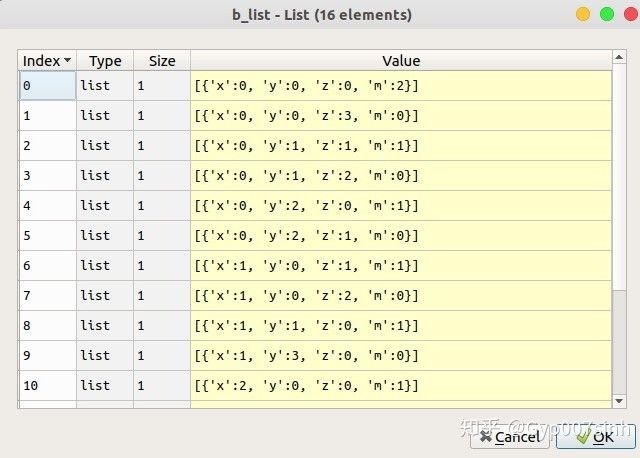
b_list=[]
d_list=[]
e_list=[]
lst=[]
for i in range(5): #该模式下切4m长的段数
for j in range(4): #该模式下切5m长的段数
for k in range(4): #该模式下切6m长的段数
for l in range(3): #该模式下切8m长的段数
if 16<=4*i+5*j+6*k+8*l<=19:
a_list = [] #存储一种情况
a_dict = {
} #存储一种情况的数据
a_dict["x"]=i
a_dict["y"]=j
a_dict["z"]=k
a_dict["m"]=l
a_list.append(a_dict)
b_list.append(a_list) #合理的切割模式
'''最多三种切割方式'''
for m1 in range(len(b_list)):
for m2 in range(len(b_list)):
for m3 in range(len(b_list)):
if m1!=m2!=m3 and m1>m2 and m1>m3 and m2>m3:
c_list=[]
b_dict={
}
b_dict["r"]=b_list[m1][0]
b_dict["s"]=b_list[m2][0]
b_dict["t"]=b_list[m3][0]
c_list.append(b_dict)
d_list.append(c_list)
n=3 #求解的变量个数
for q in range(len(d_list)):
f=np.array([1,1,1]) #目标函数的系数矩阵
a=[];b=[];c=[];d=[]
#系数矩阵第一行
a.append(-d_list[q][0]["r"]["x"])
a.append(-d_list[q][0]["s"]["x"])
a.append(-d_list[q][0]["t"]["x"])
#系数矩阵第二行
b.append(-d_list[q][0]["r"]["y"])
b.append(-d_list[q][0]["s"]["y"])
b.append(-d_list[q][0]["t"]["y"])
#系数矩阵第三行
c.append(-d_list[q][0]["r"]["z"])
c.append(-d_list[q][0]["s"]["z"])
c.append(-d_list[q][0]["t"]["z"])
#系数矩阵第四行
d.append(-d_list[q][0]["r"]["m"])
d.append(-d_list[q][0]["s"]["m"])
d.append(-d_list[q][0]["t"]["m"])
a=np.asarray(a);b=np.asarray(b);c=np.asarray(c)
A=np.array([a,b,c,d]) #约束条件的系数矩阵
B=np.array([-50,-10,-20,-15])
#创建x,个数是3
x=cp.Variable(n,integer=True)
#目标函数
objective=cp.Maximize(cp.sum(f*x))
#约束条件,其中A是4×3,x是3×1,A*x=b(b为4×1的矩阵)
constriants=[0<=x,A*x<=B]
#求解问题
prob=cp.Problem(objective,constriants)
prob.solve(solver=cp.CPLEX)
lst.append(x.value)
e_list.append(prob.value)
print(min(e_list))
lingo
model:
title cutting-stock problem;
sets:
!定义基本集合needs及其属性length,num;
needs /1..4/:length,num;
!定义基本集合cuts及其属性x;
cuts /1..3/:x;
!定义派生集合patterns及其属性r;
patterns(needs,cuts):r;
endsets
data:
length=4 5 6 8;
num=50 10 20 15;
capacity=19;
enddata
min=@sum(cuts(i):x(i));
!满足需求的约束;
@for(needs(i):@sum(cuts(j):x(j)*r(i,j))>num(i));
!合理切割模式的约束;
@for(cuts(j):@sum(needs(i):length(i)*r(i,j))<capacity);
@for(cuts(j):@sum(needs(i):length(i)*r(I,j))>capacity-@min(needs:length));
!人为增加的约束;
@sum(cuts:x)>26;@sum(cuts:x)<31;
@for(cuts(i)|i#lt#@ size(cuts):x(i)>x(i+1));
@for(cuts:@gin(x););
@for(patterns:@gin(r););
end
)<capacity);
@for(cuts(j):@sum(needs(i):length(i)*r(I,j))>capacity-@min(needs:length));
!人为增加的约束;
@sum(cuts:x)>26;@sum(cuts:x)<31;
@for(cuts(i)|i#lt#@ size(cuts):x(i)>x(i+1));
@for(cuts:@gin(x););
@for(patterns:@gin(r););
end