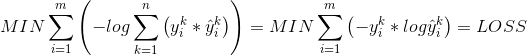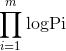深度学习中，逻辑回归(交叉熵)，softmax损失函数的推导，以及sigmoid, relu, tanh, softmax函数的用处

sigmoid, relu, tanh, softmax函数的用处

其中作为激励函数的有:

(1) g(z) = sigmoid(z) =   

(2) g(z) = relu(z) = max(0, x)

(3) g(z) = tanh(z) = 

以上激励函数作用为构造非线性模型，如:z = W^Tx + b是一个线性模型，当引入a = g(z)时，就构造出了非线性模型，用来拟合实际中的实际问题。

作为分类：

(1)sigmoid函数：用于2分类与多分类问题。

(2)softmax函数：用于多分类问题

逻辑回归(交叉熵)损失函数的推导（以二分类举例）

LOSS = ∑-y_i * log(y_hat_i) - (1 - y_i) * log(1 - y_hat_i), 其中y_hat_i = g(z_i) = sigmoid(z_i) 值介于0,1之间

对于样本x_i, 二分模型判定其为1的概率为p1_i = y_hat_i     (注：p1_i指的是第i个样本预测判定其为1的概率)

对于样本x_i, 二分模型判定其为1的概率为p0_i = 1 - y_hat_i     (注：p0_i指的是第i个样本预测判定其为0的概率)

为使得模型拟合程度最高，即对y_hat_i其值越靠近真实值y_i越好。也就是说：比如y_i = 1时，让p1_i = y_hat_i = g(z_i)越趋向于

1越好，当y_i = 0时，让p0_i = 1 - y_hat_i = 1 - g(z_i)，比如y_hat_i = 0.05是靠近0的，故p0_i = 1 - 0.05 = 0.95，即判定为0的概率的0.95.

为此我们将p1_i与p0_i合并在一起：p_i = y_i * y_hat_i + (1 - y_i) * (1 - y_hat_i)   (其中y_i为0或1)，即当y_i为0时p_i = p0_i;为1同理

为使得模型最有效，只需对于所有样本使得p_i（就是偏向第i个样本其真实类别的概率）最大即可。运用极大似然

取对数，只需 最大即可,将p_i带入化简的：其中

logPi = log[y_i * y_hat_i + (1 - y_i) * (1 - y_hat_i)]

          = log[y_i *sigmoid(z_i) + (1 - y_i) * (1 - sigmoid(z_i))]

          = log[1 + y_i * (e^z_i - 1)] - log[1 + e^z_i]

          = 

          = y_i * z_i - log(1 + e^z_i)    (合并）

而-loss = y_i * log(y_hat_i) + (1 - y_i) * log(1 - y_hat_i)

             = y_i * log(sigmoid(z_i)) + (1 - y_i) * log(1 - sigmoid(z_i))

             = y_i * z_i - log(1 + e^z_i)

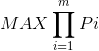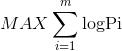即：logPi == -loss, 而我们为使得模型最有效只需等价于 ,即最小化 =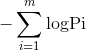 

 

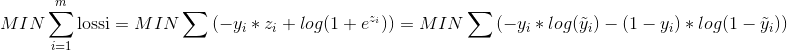
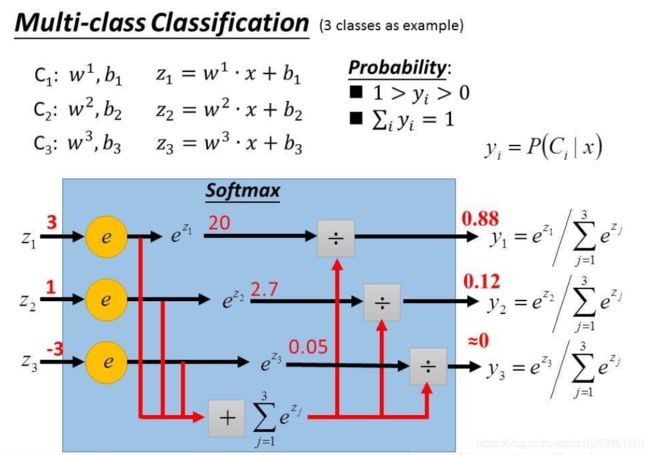
softmax损失函数的推导（以n分类举例）

 

设对于样本x_i设其有n类即y_i = 1, 2, ..., n.

我们采用one hot的方式进行标识：比如

就拿以上例子，为使得模型有效，我们举一个合适的预测分类的one hot: 0.01 0.05 0.01 0.92 0.01

y_i_k_hat :标是对y_i的预测one hot形式第k分量的值，比如以上例子k = 4时，y_i_k_hat = 0.92   ()

为使得y_i_hat向量尽可能接近y_i向量，对于x_i， p_i = ∑y_i_k * y_i_k_hat (其中k从1到n), 上式子标是对于x_i，预测其为y_i的概率。比如y_i = 4时，y_i_k == 0 （k = 1,2,3,5）, y_i_k = 1 (k = 4)

为使得模型最有效，只需对所有样本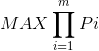即可，等价于 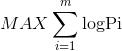,即最小化 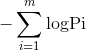=