【数据结构与算法（六）】——树（复杂的树）

这是第六天，昨天是周天，做了课程相关实验，收获还是蛮多的，但是过程很曲折，做了很多不必要的工作。
树的最常见的相关算法就是使用递归，因为对于一整个树，其左子树或右子树同样是一个完整的树。
直接或间接的遍历考查，所以要将复杂的题简单化。而且对于树，最最需要小心的是指针的操作，树中有大量的指针操作。在每次使用指针的时候，都要问自己这个指针有没有可能是nullptr，如果有可能的话，那该怎么处理。
画图！画图！画图让思路清晰
接下来，每天四道算法题，不太多也不太少

树（进阶）

树的更复杂的算法，对一些简单遍历或者排序的变形；还有一些特别的树，堆或者红黑树之类的。

题目

树的子结构

输入两棵二叉树A和B，判断B是不是A的子结构。

思路：

1、主要分为两步：①在树A中找到和树B一样的根节点；②判断树A的该“根”节点的子树的结构是否和树B一样
2、第一步在树A中找到和树B的根节点一样的节点，这其实就是树的遍历，可以使用递归的方式
3、第二步判断树A中以R为根节点的子树是不是和树B有相同的结构。同样用递归（所以说不是到达这一步就不用怕段根节点是否相同了，你第一次进来不用判断，但是后面的递归进来之前是没有判断传进来的两个值是否相等的）：如果节点R的值和树B的根节点不相同，则以R为根节点的子树和树B肯定不具有相同的结构；

//从树A中找结构为树B的子树
//第二步：在树A中找到与B的子树一样的结构的子树
bool DoesTree1HaveTree2(BinaryTreeNode* rootA, BinaryTreeNode* rootB)
{
    //递归结束的条件就是B走到尽头啦
    if (rootB == nullptr)
        return true;
    if (rootA == nullptr)   //B还没有结束A就结束了，当然就没有找到一样的子树了
        return false;   
    if (rootA->value != rootB->value)
        return false;
    //找到一样的根节点了，继续判断它的左子树和右子树
    return DoesTree1HaveTree2(rootA->leftNode, rootB->leftNode) && DoesTree1HaveTree2(rootA->rightNode, rootB->rightNode);
}

//第一步：遍历树A，找到与树B的根节点一样的节点
//函数返回的时候，rootA指针指向的内存没有改变，内存里面的东西也没有改变
bool HasSubTree(BinaryTreeNode* rootA, BinaryTreeNode* rootB)
{
    bool result = false;
    if (rootA != nullptr&&rootB != nullptr) {
        if (rootA->value == rootB->value)
            result = DoesTree1HaveTree2(rootA, rootB);
        //如果没有找到一样的根节点或者找到一样的根节点后它的子树和B不一样就继续往左子树找
        if (!result)
            result = HasSubTree(rootA->leftNode, rootB);
        //在左子树中还是没有找到符合条件的子树就往右子树找
        if (!result)
            result = HasSubTree(rootA->rightNode, rootB);
    }
}

测试用例：
1、树A和树B的头节点有一个或者两个都是空指针（空树）
2、在树A或树B中所有节点都只有左子节点或右子节点
3、正常的树（树B不是或者是树A的子树）
这里有一个要注意的东西就是关于double、float类型的值是否相等的比较。计算机内表示小数时都有误差。判断两个小数是否相等，只能判断它们之差的绝对值是不是在一个很小的范围内。如果两个树的差很小，就可以认为它们是相等的。double类型比较使用的函数为

//double类型比较，float类型也相似
bool doubleIsEqual(double num1, double num2)
{
    if (num1 - num2<0.0000001 || num1 - num2>-0.0000001)
        return true;
    else
        return false;
}

二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。假设输入的数组的任意两个数字都不相同

思路：以{1，4，3，6，9，8，5}为例

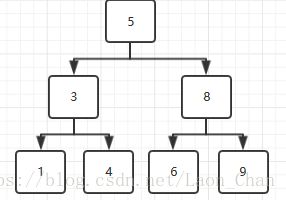
1、在二叉搜索树中，分为两个部分：第一部分左子树节点的值，它们都要比它们的根节点的值要小；第二部分右子树节点的值，它们都要比它们根节点的值要大
2、在后序遍历序列中，最后一个数值就是整棵树的根节点的值。在例子中，5是最后一个数，所以5是根节点的值。在这个数组中，前3各元素1，4，3都要比5小，所以1，4，3是整棵树的以5为根的左子树的节点；后三个元素6，9，8都比5大，所以6，9，8都是以5为根的右子树中的节点
3、用递归的方法同样可以确定子数组对应的树的结构，在{1，4，3}子数组中，3是最后一个数，所以3是左子树的根节点；1比3小，所以1是以3为根节点的左子树的节点；4比3大，所以4是以3为根节点的右子树的节点。右子树对应的子数组{6，9，8}方法类似
4、再来分析一个数组{7，2，5，3}。后序遍历的最后一个元素3是根节点。由于第一个元素7大于3，所以在对应的树结构没有右子树，即7后面的数2和5都是以3为根节点的树的右子树中的节点。但是我们经过判断，其中的元素2小于3，这不符合二叉搜索树中“右子树的节点都大于根节点”这一个规则，所以数组{7，2，5，3}不是一个二叉搜索树的后序遍历序列

bool isSequenceBST(int sequence[], int length)
{
    //这是一个空序列空数组,直接就可以退出此次判断了
    if (sequence == nullptr ||  length <= 0)
        return false;
    //如果不是空序列则继续
    int root = sequence[length - 1];//根是最后一个元素
    //在二叉搜索树中左子树的节点都小于根节点,找到小于根节点的最后一个元素
    int i;
    for (i = 0; i < length - 1; i++)
        if (sequence[i] > root)
            break;      //注意是break，只是为了找到最后一个左子树节点
    //在二叉搜索树中右子树的节点都大于根节点，接着左子树的最后一个元素之后的元素判断
    //看之后的所有元素是否都大于根节点，如果小于的话说明这个树不是搜索二叉树
    int j;
    for (j = i; j < length - 1; j++)
        if (sequence[j] < root)
            return false;
    //判断左子树是不是二叉搜索树
    bool left = true;   //为什么一开始就true？因为要是没有左子树就直接不用判断啦，就直接是true了
    if (i > 0)
        left = isSequenceBST(sequence, i);
    bool right = true;
    if (i != length - 1)
        right = isSequenceBST(sequence + i, length - i - 1);//length-i-1是减去左子树和根节点

    return (left&&right);
}

测试用例：
1、输入一个后序遍历序列有对应的二叉树（二叉树有左右节点；所有节点都左子节点或右子节点；只有一个节点的二叉树）
2、输入的后序遍历序列没有对应的二叉树
3、输入一个空的序列，sequence=nullptr
无论是后序遍历序列还是前序遍历、中序遍历序列的处理，都要首先分析序列的特点，比如前序遍历序列的第一个节点就是根节点。之后最好画图或者举一个特殊的容易看得懂的例子进行分析，在开始coding还要想一下测试用例，特别的序列和特别的树都要想到，即特殊的输入和特殊的输出

二叉树中和为某一值的路径

输入一棵二叉树和一个整数，打印出二叉树中节点值的和为输入整数的所有路径。从树的根节点开始往下一直到叶节点所经过的节点形成一条路径。

思路：

1、举个例子理解题目的意思：输入的二叉树如下图所示，输入的整数为13，那么打印出来的路径有两个{5，8}和{5，6，2}

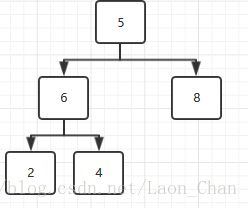
2、路径必须是从根节点出发最后达到叶节点。这样，根节点就是输出的路径的起始节点，所以要从根节点开始遍历
3、当用前序遍历的方式访问到某一个节点时，我们把该节点添加到路径上，并累加该节点的值。如果该节点为叶节点，并且路径中节点值的和刚好等于输入的整数，则当前路径符合要求，可以把它打印出来。如果当前节点不是叶节点，则继续访问它的子节点
4、访问到叶节点后，访问结束，递归函数将自动回到它的父节点，因此我们在函数退出之前要删除路径上的当前节点并将和减去当前节点的值，以确保返回父节点时路径刚好是从根节点到父节点
5、可以看出，保存路径的数据结构是一个栈，因为路径要与递归调用状态一致，而递归调用就是一个压栈和出栈的过程。

void FindPath(BinaryTreeNode* root, int expectedSum)
{
    if (root != nullptr)
        return;
    std::vector<int> path;//为什么不用stack？后面会说
    int currentSum = 0;
    FindPath(root, expectedSum, path, currentSum);
}

void FindPath(BinaryTreeNode* root, int expectedSum,std::vector<int>& path, int currentSum)
{
    currentSum += root->value;
    path.push_back(root->value);
    //如果是叶节点，并且路径上节点值的和等于输入的期望值。打印出当前路径
    bool isLeaf = root->leftNode == nullptr&&root->rightNode == nullptr;
    if (currentSum == expectedSum && isLeaf) {
        cout<<"找到一条路径："<std::vector<int>::iterator it;   //这里就说明了为什么不用stack
        for (it == path.begin(); it != path.end(); it++)
            cout << *it << "\t";
        cout << endl;
    }
    //如果不是叶节点，则继续遍历它的子节点
    if (root->leftNode != nullptr)
        FindPath(root->leftNode, expectedSum, path, currentSum);
    if (root->rightNode != nullptr)
        FindPath(root->rightNode, expectedSum, path, currentSum);

    //在返回到父节点前，在路径上删除当前节点？？？这是啥？
    //遍历到叶节点之后要返回到父节点，从最最最上面一层，也就是叶节点-叶节点的父节点-……
    //开始一层层进入到最后一层后再叶开始一层层剥开，递归要画图
    path.pop_back();
}

为什么不用栈？在stack中只能得到栈顶元素，而我们在打印路径的时候需要的只是得到路径上的所有节点，而不删除它们，因此用stack会使得每次打印完一条路径之后，就得完完全全从根节点重新开始。
测试用例：
1、二叉树中有一条符合要求的路径
2、二叉树中没有符合要求的路径
3、二叉树的根节点为nullptr

二叉树的深度

输入一棵二叉树的根节点，求该树的深度。从根节点到页节点依次经过的节点（含根、叶节点）形成树的一条路径，最长路径的长度为树的深度

思路：

如果一棵树只有一个节点，那么它的深度就是1。如果根节点只有左子树没有右子树，那么树的深度就是其左子树的深度加1；同样如果只有右子树而没有左子树，那么树的深度就是其右子树的深度加1.如果既有左子树又有右子树，那么树的深度应该就是左右子树中深度较大的那个值加1。又是树，又是遍历，所以就可以用递归的方法来解决这个问题了——要想得到一整棵树的深度，就必须计算其右子树和左子树的深度并进行比较之后加1，而计算左/右子树的深度，又得从其对应的子树计算得到较深的一个值，所以就是递归了。从子树—》树

//起始递归的思想很简单的，为什么有时候我会把它想得那么复杂；要准确分析退出递归的条件
//递归从根往叶调用函数，之后从页往根返回
//只要不是空指针，每次返回都会累加。
int depthTree(BinaryTreeNode* root)
{
    if (root == nullptr)
        return 0;
    int depthLeft = depthTree(root->leftNode);
    int depthRight = depthTree(root->rightNode);

    return (depthLeft > depthRight) ? (depthLeft + 1) : (depthRight + 1);
}

平衡二叉树

输入一棵二叉树的根节点，判断该树是不是平衡二叉树。如果某二叉树中任意节点的左、右子树的深度相差不超过1，那么它就是一棵平衡二叉树。【概念】

思路：

1、因为是所有节点的左右子树的深度都要计算到，所以可以使用上面的计算树的深度的函数，每次计算得到当前节点的两个子树的深度后都要进行比较，如果不符合要求就可以退出递归了，整个递归退出过程都是返回false。

bool isBalanced(BinaryTreeNode* root)
{
    //节点不存在，不存在平不平衡这个问题
    if (root == nullptr)
        return true;
    //要判断这个节点是否平衡，必须分别得到左右子树的深度
    int depthLeft = depthTree(root->leftNode);
    int depthRight = depthTree(root->rightNode);
    int diff = depthLeft - depthRight;
    if (diff >= 1 || diff <= -1)
        return false;
    //之后再一个一个遍历其他节点，计算、比较、判断
    return isBalanced(root->leftNode) && isBalanced(root->rightNode);
}

2、上面的方法代码很简洁，但是需要多次遍历同一个节点，在判断父节点的时候要分别计算子树深度，这是第一次遍历；之后在判断该节点的时候，又要再一次调用depthTree函数对下面的节点进行再一次遍历
如果使用后序遍历的方式遍历二叉树的每一个节点，那么在遍历到一个节点之前我们就已经遍历了它的左、右子树。只要在遍历每个节点的时候记录它的深度（某一个节点的深度等于它到叶节点的路径的长度），就可以一边遍历一边判断该节点是不是平衡的。

//只有一次遍历：因为每次遍历都记录了遍历的树的深度，所以等到计算它的父节点的树的深度只要加1就好了
bool isBalanced(BinaryTreeNode* root,int* pDepth)
{
    if (root == nullptr) {
        *pDepth = 0;
        return 0;
    }

    int left, right;
    if (isBalanced(root->leftNode, &left) && isBalanced(root->rightNode, &right)) {
        int diff = left - right;
        if (diff <= 1 || diff >= -1) {
            *pDepth = 1 + (left > right) ? left : right;
            return true;
        }
    }
    //如果调用isBalanced的时候有返回过false，说明就不需要进入比较了，因为说明已经有一个节点事不平衡的了
    return false;
}

主要是使用引用记录了其左右子树的深度，至于所说的后序遍历？应该只是用到了后序遍历的思想，递归的话就你要知道你左右子树的深度，就得先知道你的左子节点对应的左右子树的深度，所以这样就是必须得先遍历左子树和右子树，左子节点又得先遍历左子树和右子树，然后记录深度这样，最重要的还是弄懂递归到底在干嘛
测试用例：
还是从特殊输入和输出入手，还有就是注意空指针、空树
1、平衡二叉树
2、非平衡二叉树
3、二叉树所有节点都没有左/右子树
4、二叉树只有一个节点
5、空树