博弈中的对抗搜索问题
博弈（Game）
- 多智能体环境下，智能体之间存在合作和竞争关系；
- 数学领域中的“博弈”： 把任何多智能体环境看成是一种博弈游戏，如果其中每个智能体对其它智能体的影响是“显著的”，这些影响可以是合作或竟争。
- 人工智能领域中的“博弈”： 确定性的、有完整信息的，轮流行动的，两个游戏者的零和游戏。
- 博弈的抽象本性成为AI研究者感兴趣的对象
AI中研究的博弈，即如何根据当前的棋局，选择对自己最有利的一步棋 ？
博弈的特点：
双方的智能活动，任何一方都不能单独控制博弈过程，而是由双方轮流实施其控制对策的过程。
博弈问题的表示：
用博弈树来表示，它是一种特殊的与或图。节点代表博弈的格局（即棋局），相当于状态空间中的状态，反映了博弈的信息。 与节点、或节点隔层交替出现。
为什么与节点、或节点隔层交替出现？
假设博弈双方为：MAX和MIN
在博弈过程中，规则是双方轮流走步。在博弈树中，相当于博弈双方轮流扩展其所属节点。
从MAX方的角度来看：所有MIN方节点都是与节点
理由： 因为MIN方必定选择最不利于MAX方的方式来扩展节点，只要MIN方节点的子节点中有一个对MAX方不利，则该节点就对MAX方不利，故为“与节点”。
从MAX方的角度来看：所有属于MAX方的节点都是“或节点”
理由： 因为扩展MAX方节点时，MAX方可选择扩展最有利于自己的节点，只要可扩展的子节点中有一个对已有利， 则该节点就对已有利。
在博弈树中，先行一方的初始状态对应树的根节点，而任何一方获胜的最终格局为目标状态，对应于树的终叶节点（可解节点或本原问题）。但是，从MAX的角度出发，所有使MAX获胜的状态格局都是本原问题，是可解节点，而使MIN获胜的状态格局是不可解节点。
博弈的例子：
- 一字棋
- 跳棋
- 中国象棋
- 围棋
- 五子棋
博弈中的优化决策(Optimal decisions)
- 问题的表述：两名游戏者MAX和MIN，MAX先行，然后两人轮流出招，直到游戏结束。
- 在游戏的最后，给优胜者奖分，给失败者罚分。
- 该问题可以形式化成为下面的搜索问题：
初始状态：包括棋盘局面和确定该哪个游戏者出招；
后继函数：返回(move, state)的一个列表；（move是合法招数，state是招数move所导致的状态）
终止测试：判断游戏是否结束；结束的状态称为终止状态
目标函数：对终止状态给出一个数值。
例：井子棋游戏
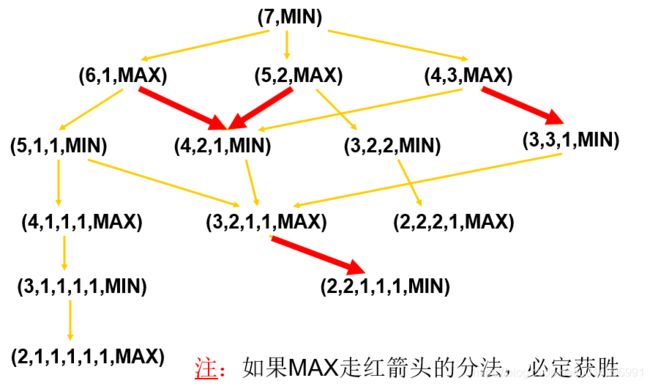
例：Grundy博弈-分配物品问题
如果有一堆数目为N的钱币，由两位选手轮流进行分配，要求每个选手每次把其中某一堆分成数目不等的两小堆，直至有一选手不能将钱币分成不等的两堆为止，则判定这位选手为输家。
用数字序列加上一个说明来表示一个状态：
(3, 2, 1, 1, MAX)
数字序列：表示不同堆中钱币的个数
说明：表示下一步由谁来分，即取MAX或MIN
现在取N＝7的简单情况，并由MIN先分
对于比较复杂的博弈问题，只能模拟人的思维“向前看几步”，然后作出决策，选择最有利自己的一步。即只能给出几层走法，然后按照一定的估算办法，决定走一好招。
决策过程
- 将当前状态作为初始状态，建立一个深度为h的搜索树，h（horizon，称为视野）是在有限时间内能够考虑到的最大深度
- 对所有叶节点状态进行评价
- 由叶节点回推至根节点，选择其中最好的一个动作决策（假设对手MIN的应对总是给MAX带来最坏的结果）
极大极小算法 Minimax algorithm
评价函数 Evaluation Function
- 函数 e: 状态 s 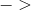数值 e(s)
- e(s) 即为估计状态s对于MAX来说“好”的程度的启发式信息
- e(s) > 0 意味着状态s对于MAX来说是有利的 (数值越大越有利)
- e(s) < 0意味着状态s对于MIN来说是有利的
- e(s) = 0 意味着状态s是中立的
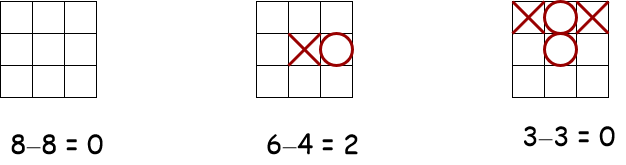
例: 井字棋
e(s) = 对MAX开放的行，列，对角线数量 - 对MIN开放的行，列，对角线数量
值的回推
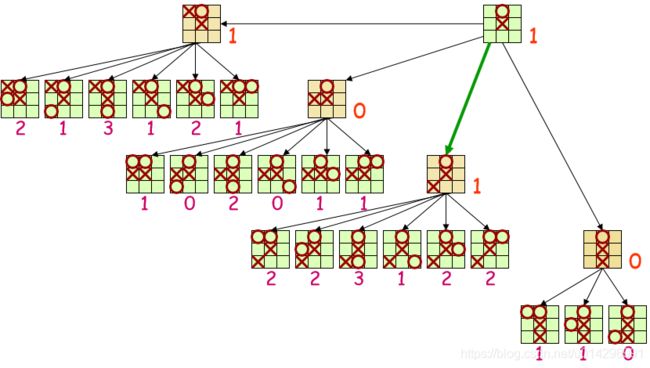
深度为2的搜索树
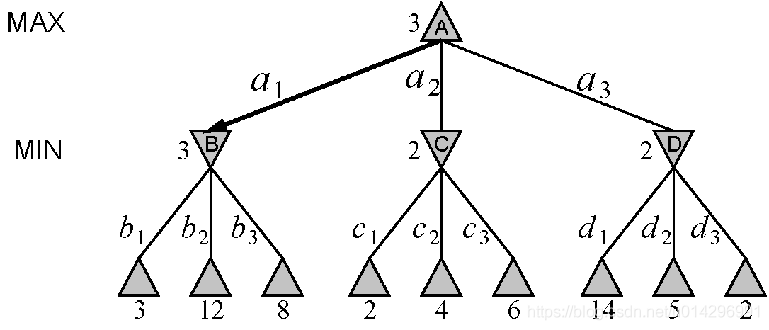
MiniMax反推过程
- 假设评价值越高，对Max越有利；评价值越低，对Min越有利；
- 反推过程中，对每一个节点赋予一个值，这个值是在对方不犯错误的情况下，自己能够获得的最大受益。
MiniMax决策过程
- 在Max步中，Max选择能够得到MiniMax值最大的状态的行动；
- 在Min步中，Min选择能够得到MiniMax值最小的状态的行动。
- 这样便完成了博弈中的决策过程。
反推与决策过程示例
极大极小算法
- 从当前状态（MAX走棋）开始，扩展博弈树到深度h （视野: 因为需要在时间限制内做出决策）
- 对博弈树的每一个叶节点计算评价函数值
- 由叶节点开始至根节点计算回推值： (a)MAX节点取得其后继的最大评价值 (b)MIN节点取得其后继的最小评价值
- 选择能够得到最大回推值的走棋
伪代码：
function MINIMAX-DECISION(state) returns an action
inputs: state, current state in game
return the a in Actions(state) maximizing MIN-VALUE(RESULT(a,state))
function MAX-VALUE(state) returns a utility value
if TERMINAL-TEST(state) then return UTILITY(state)
v <- -INF
for a,s in SUCCESSORS(state) do v<-MAX(v,MIN-VALUE(s))
return v
function MIN-VALUE(state) returns a utility value
if TERMINAL-TEST(state) then return UTILITY(state)
v <- INF
for a,s in SUCCESSORS(state) do v<-MIN(v,MAX-VALUE(s))
return v 博弈过程 (MAX)：
到达最终状态前重复以下步骤
- 采用极大极小方法选择一步走棋
- 按1的决策走棋
- 观察MIN的应对走棋
注意：每一回合建造深度为h的博弈树仅为选择当前的一步走棋，下一个回合重复所有的步骤（上一回合中深度为h-2的子树可以拿来重复使用）
α-β 剪枝(α-β pruning)
极大极小搜索过程由两个完全分离的步骤组成：
- 用深度优先算法生成一棵博弈搜索树。
- 估计值的倒推计算。
缺点：这种分离使得搜索的效率比较低。
还能做得更好吗？
是的 ! 能够做得更好 !
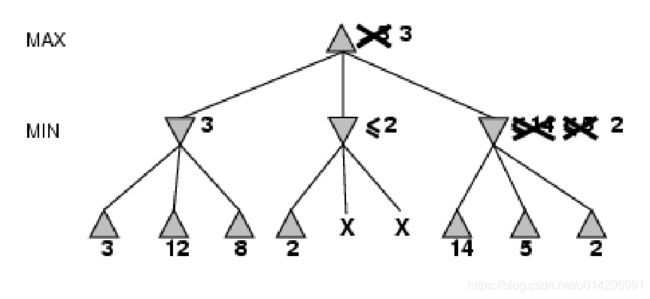
例子：
改进：在博弈树生成过程中同时计算端节点的估计值及倒推值，以减少搜索的次数，这就是α-β过程的思想，也称为α-β剪枝法。
α-β 剪枝：
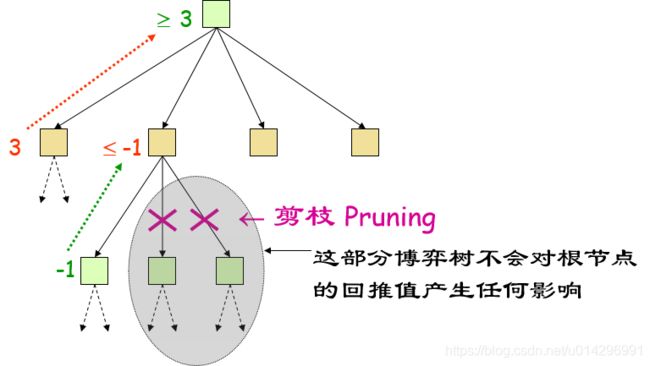
- 剪枝：剪掉那些不影响最后决策的分支。
- 一般原则：考虑某节点n，如果游戏者在n的上层的任何节点有一个更好的选择m，那么再计算的MiniMax值就与n无关，即n可以被剪裁掉。
α-β 剪枝的思想：如果m比n好，我们就不会走到n。
例：
α-β
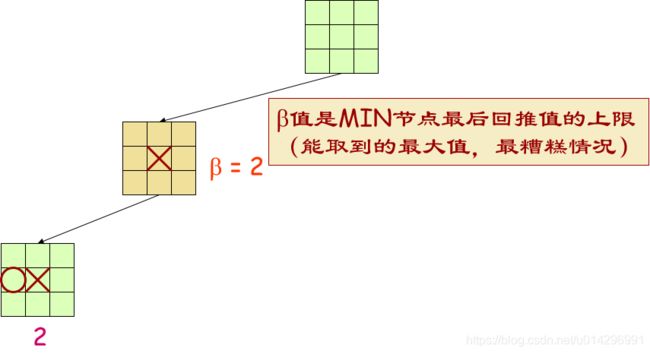
- α＝到目前为止我们在路径上的任意选择点发现的MAX的最佳选择
- β＝到目前为止我们在路径上的任意选择点发现的MIN的最佳选择
α-β 剪枝：
- 当某个节点的值比目前MAX的α值或MIN的β值更差时，裁掉该节点剩下的分支。
- 剪枝不影响最后得到的结果。
- α-β剪枝的效率很大程度上取决于检查后继的顺序
伪代码：
function ALPHA-BETA-DECISION(state) returns an action
inputs: state, current state in game
return the a in ACTIONS(state) maximizing MIN-VALUE(RESULT(a,state))
function MAX-VALUE(state,alpha,beta) returns a utility value
inputs: state, current state in game
alpha, the value of the best alternative for MAX along the path to state
beta, the value of the best alternative for MIN along the path to state
if TERMINAL-TEST(state) then return UTILITY(state)
v <- -INF
for a,s in SUCCESSORS(state) do
v<-MAX(v,MIN-VALUE(s,alpha,beta))
if v >= beta then return v
alpha <- MAX(alpha,v)
return v
function MIN-VALUE(state,alpha,beta) returns a utility value
same as MAX-VALUE but with roles of alpha,beta reversed处理搜索树中的重复状态
- 在游戏中重复状态的频繁出现往往是因为调换—导致同样棋局的不同行棋序列的排列
例如，[a1, b1, a2, b2]和[a1, b2, a2, b1]都结束于同样的棋局，其中[b1, b2]是[b2,b1]的调换。
- 解决办法：第一次遇见某棋局时将对它的评价存储在哈希表中（该哈希表称为调换表）。
实战：https://blog.csdn.net/u014296991/article/details/105618765
不完整的实时决策(Imperfect, real-time decisions)
- α-β算法依然要搜索至少一部分空间直到终止状态，这样的搜索不现实。
- 用可以估计棋局效用的启发式评价函数EVAL代替评估终止节点的效用函数。
- 用可以决策什么时候运用EVAL的截断测试取代终止测试。
如何设计评价函数？
- 应该以和真正的效用函数同样的方式对终止状态进行排序。
- 评价函数的计算不能花费太多的时间。
- 对于非终止状态，评价函数应该和取胜的实际机会密切相关。
- 在计算能力有限情况下，评价函数能做到最好的就是猜测最后的结果
- 大多数评价函数的工作方式是计算状态的不同特征，那么对状态的一个合理评价是加权平均值
国际象棋中EVAL通常取为加权线性函数（假设每个特征的贡献独立于其它特征的值）
截断搜索
- 用 CUTOFF-TEST(state, depth) 来进行截断测试，如果满足则返回 EVAL(state)；
- 使用迭代深入搜索：当时间用完时，程序就返回目前完成最深的搜索所选择的招数。
- 由于评价函数的近似性，截断搜索可能导致错误。
截断搜索的改进
- 需要更为复杂的截断测试：
评价函数应该只用于那些静止的棋局（近期不会出现大的变化的棋局），非静止的棋局可以进一步扩展直到静止的棋局，这种额外的搜索称为静止搜索。
期望搜索和MTD(f)
- 普通的Alpha-Beta搜索对某个局面最终的“最小-最大”值没有假设。看上去它考虑到任何情况，但是，如果你有一个非常好的主意(例如由于你在做迭代加深，从而想到前一次的结果)，你就会找出那些和你预期的差得远的路线，预先把它们截断。
- Alpha-Beta搜索的一个变种，开始时用从负无穷大到正无穷大来限定搜索范围，然后在期望值附近设置小的窗口
- 设想发表在一个网站上：http://theory.lcs.mit.edu/~plaat/mtdf.html
- 具体实现称为MTD(f)搜索算法，只有十多行
残局库 Endgame Databases
- 残局库在很多棋类游戏中扮演着非常重要的角色。例如九人Morris，西洋跳棋。
- 要让某种棋类完全可解，通常要借助于残局库——从起始局面开始向前搜索，结合残局库，就能解出这盘棋。
- 在盘面上棋子数量很少的情况下，残局库才能实现。国际象棋5子残局—7.05GB存储空间，6子残局库—1.2TB！
残局库类型
- 如果残局库中某个特定的局面是赢棋、输棋还是和棋是确定的，称为“胜负和”（WLD）残局库；
- 如果知道多少步以后棋局会结束，称为“杀棋步数”（DTM，Distance to Mate）残局库；
- 如果只知道多少步以后会转换为另一种类型的局面，就称为“转换步数”（DTC，Distance to Conversion）残局库。
残局库生成
- 基本算法称为“后退式分析”(Retrograde Analysis)，由Ken Thompson首先使用
- 从某个已知棋局结果的状态回退（eg：白方被将死），推测前一步黑方是如何走棋达到该状态的
注：主要内容来自巢文涵老师的人工智能课