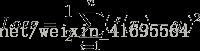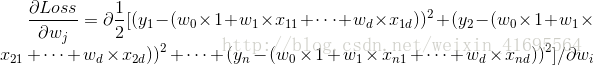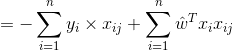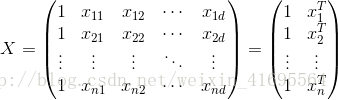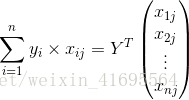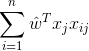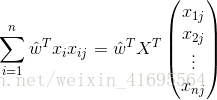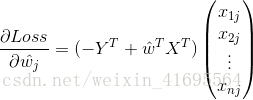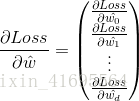机器学习笔记（三）——Logistic Regression 的原理以及代码实现

        假设现在有一些数据点，我们用一条直线对这些点进行拟合（该线称为最佳拟合直线），这个拟合过程就称作回归。利用Logistic 回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类。这里的“ 回归“一词源于最佳拟合，表示要找到最佳拟合参数集，其背后的数学分析将在下面介绍。训练分类器的做法就是寻找最佳拟合参数，使用的是梯度下降法，本文首先阐述Logistic 回归的定义，然后推导回归系数的迭代公式，最后给出一个Logistic 回归的实例，使用python 3.6编写代码，根据肿瘤的形状数据来预测肿瘤的良恶性。

一、Sigmoid函数的介绍

        Logistic Regression是线性回归，但最终是用作分类器：它从样本集中学习拟合参数，将目标值拟合到[0,1]之间，然后对目标值进行离散化，实现分类。

        为什么叫Logistic呢？因为它使用了Logisitic函数（又称为Sigmoid函数），这个Sigmoid函数将分类任务的真实标记和线性回归模型的预测值联系起来。Sigmoid函数具体的计算公式如下：

首先我们来看一下Sigmoid函数在不同坐标尺度下的两条曲线图，下面是绘制曲线图的python代码：

import numpy as np
import matplotlib.pyplot as plt

def sigmoid( inx ):
    """
    这是sigmoid函数
    """
    return 1.0/(1+np.exp(-inx))

x_value = np.linspace(-6,6,20)
y_value = sigmoid( x_value )
xx_value = np.linspace(-60,60,120)
yy_value = sigmoid( xx_value )
  #numpy模块中的linspace()函数与arange()函数非常相似。它的前两个参数同样是用来指定序列的起始和结尾，
  #但是第三个参数不再表示相邻两个数字之间的距离，而是用来指定我们想把由开头和结尾两个数字所指定的范围分成几个部分。
fig = plt.figure()
ax1 = fig.add_subplot(211)
ax1.plot( x_value,y_value )
ax1.set_xlabel('x')
ax1.set_ylabel('sigmoid(x)')
ax2 = fig.add_subplot(212)
ax2.plot( xx_value,yy_value )
ax2.set_xlabel('x')
ax2.set_ylabel('sigmoid(x)')
plt.show()

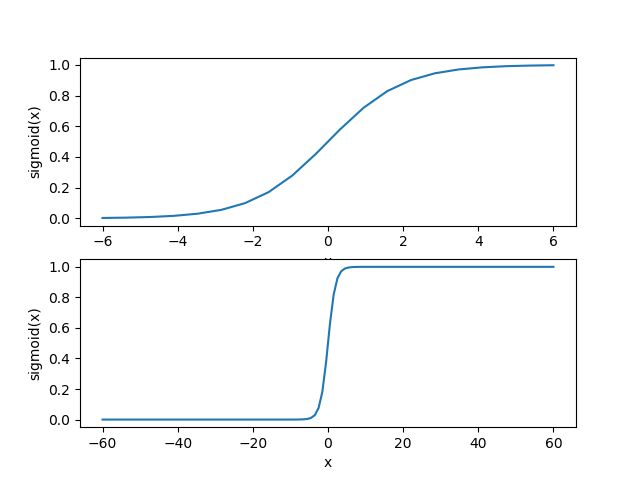
         得到两种坐标尺度下的Sigmoid函数图，如下所示，其中上图的横坐标为-6到6，这时的曲线变化较为平滑；下图横坐标的尺度足够大，可以看到，在x=0点处Sigmoid函数看起来很像单位阶跃函数。而这种类似于阶跃函数的效果正是我们想要的，考虑二分类任务，其输出标记为0和1，而Sigmoid函数将z值转化为一个接近0或1的y值，并且其输出值在z = 0附近变化很陡。

       Sigmoid函数的输入记为z，暂且又下面公式表出：

其中表示示例在属性上面的取值。因此，为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计。

        为了使得分类器尽可能地精确，我们需要找到最佳参数（系数），然而，为了找到最佳参数（系数），需要用到最优化理论的一些知识。

二、线性回归的基础

        给定包含个示例的数据集，其中，其中是在第1个属性上的取值（括号中的‘;’表示这是一个列向量，‘，’表示这是行向量，下同），。”线性回归“试图学得一个线性模型以尽可能准确地预测实值输出标记。

        线性模型试图学得一个通过属性的线性组合来进行预测的函数，即

一般用向量形式写出

 

其中

。

为了便于讨论，我们把和吸收入向量形式，变成的形式。 因此，我们重新得到

 

其中

        如何确定和呢？显然关键在于如何衡量和之间的差别。均方误差（亦称为平方损失）是回归任务中最常用的性能度量，因为它求导方便，做梯度优化的时候计算便捷。误差形式如下

         显然此公式是二次方程，有最小值，当它取最小值得时候，所对应的就是最佳拟合参数。求解使最小化的过程，称为线性回归模型的最小二乘”参数估计“。

三、梯度下降法求解优化问题

       梯度下降法基于的思想是；要找到某函数的最小值，最好的方式就是沿着该函数的梯度方向的反方向搜寻。

        其步骤是，先随机给赋值，然后沿着公式一阶偏导的反方向计算下降量值，多次重复，最终会让公式收敛到一个极小值。用向量来表示的话，梯度下降法的迭代公式如下：

其中，是步长，即每次迭代的移动量的大小。

由于涉及到矩阵的计算，比单变量情形要复杂一些，下面我们做一个简单的讨论：

 我们先来求解，推导过程如下：

                 

                                                

        前面我们为了便于讨论，已经把和吸收入一个向量当中，相应的，把数据集表示为一个大小的矩阵，其中每行对应于一个示例，该行后个元素对应于示例的个属性值，第一个元素恒置为1，即

再把标记也写出向量形式，因此上面推导过程最后一步可以写为

同理，可以表示为

所以，误差的一阶偏导可以写成 

  

综上所述，我们把写成矩阵的形式，如下所示

                                                                                      

 

结合   以及转置矩阵的运算规律和，得到以梯度下降法计算最优的迭代公式为：

四、Logistic Regression的代码实现

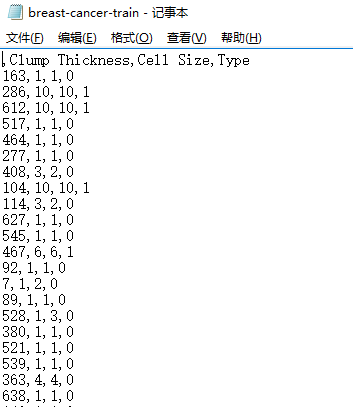
        上一节我们用梯度下降法推导出的迭代公式，现在我们结合实例来实现逻辑回归。本节将使用Logistic Regression来预测肿瘤的良恶性问题。这里的数据包含699个样本数据，我们把样本数据分为训练集（524个样本）和测试集（175个样本），并以csv的格式存在两个不同的文件中，如下所示：

部分数据如下所示：

接下来我们编写两个加载数据集的函数，一个用来加载训练集，另一个用来加载测试集，代码如下所示：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif']=['simHei']
#这句话用来设置 matplotlib.pyplot模块绘制的图中正常显示中文字体
plt.rcParams['axes.unicode_minus']=False
#这句话用来设置 matplotlib.pyplot模块绘制的图中正常显示负号

###################################
#####   theme:逻辑回归实战    #####
####     author：行歌      #######
####    time：2018.3.11    ######
################################

def loadTrainDataSet(file_name):
    """
    此函数用来向csv格式的文件中加载训练数据，并以数组的形式输出训练集和类别标签。
    输入： file_name1是训练集所在的相对地址
    输出： trainDateArr是训练数据集（524*3的数组形式）
          trainLabelArr是训练集的类别标签（1*524的数组形式）
    """
    trainData = pd.read_csv(file_name)
    trainDate_1 = trainData[['Clump Thickness','Cell Size']].values
    trainLabelArr = trainData[['Type']].values.ravel()
    bias_item_train =  np.mat([1.0]*trainDate_1.shape[0]).T
    trainDateArr = np.hstack((bias_item_train,trainDate_1)).A
    return trainDateArr, trainLabelArr


def loadtestDataSet(file_name):
    """
    此函数用来向csv格式的文件中加载测试数据，并以数组的形式输出测试集和类别标签。
    输入： file_name1是测试集所在的相对地址
    输出： testDateArr是测试数据集（175*2的数组形式）
          testLabelArr是测试集的类别标签（1*175的数组形式）
    """
    testData = pd.read_csv(file_name)
    testDateArr_1 = testData[['Clump Thickness','Cell Size']].values
    testLabelArr = testData[['Type']].values.ravel()
    bias_item_test = np.mat([1.0] * testDateArr_1.shape[0]).T
    testDateArr = np.hstack(( bias_item_test,testDateArr_1)).A
    return testDateArr, testLabelArr

加载完数据我们打印一下训练集和类别标签，如下所示：

训练集数组的第一列全为1.0，它们对应线性回归方程中的偏置项，前面我们讲过。

接下我们编写函数来根据输入的训练集来计算回归系数，代码如下：

def sigmoid( inx ):
    """
    这是sigmoid函数
    """
    return 1.0/(1+np.exp(-inx))


def calculate_regression_coefficient( DateArr, LabelArr ):
    """
    此函数用来计算线性回归中的回归系数
    输入： DateArr是数组形式的样本集
          LabelArr是样本集对应的类别标签 
    输出: weight_vector是回归系数向量
    """
    m, n = DateArr.shape
    LabelArr =  LabelArr.reshape(m,1)
    alpha = 0.001
    max_iterations = 500
    weight_vector = np.ones((n,1))
    for i in range( max_iterations ):
        h = sigmoid( np.dot(DateArr, weight_vector) )
        error = ( LabelArr - h )
        weight_vector = weight_vector + alpha *  np.dot(DateArr.T, error)
    return weight_vector

将训练集代入其中，可以得到回归系数如下所示：

现在我们已经得到回归系数，也就意味着我们得到逻辑回归模型了，于是，我们编写函数预测测试集样本的类别，并与真实类别相比较，计算出错误率或者正确率，同时将测试集样本在散点图中展出，根据回归系数，画出不同类别数据之间的分隔线。代码如下所示：

def classifyVector(inx,weight_vector ):
    """
    此函数以回归系数和特征向量作为输入来计算对应的Sigmoid值。如果Sigmoid值大于0.5，则函数返回1，否则返回0
    """
    prob = sigmoid( np.sum(inx * weight_vector))
    if prob > 0.5:
        return 1.0
    else:
        return 0.0


def calculata_errorRate( testDateArr, testLabelArr, weight_vector ):
    """
    这个函数根据测试集的样本，计算分类错误率 
    """
    prob_Arr = sigmoid(np.dot( testDateArr,weight_vector ))
    label_result = np.zeros((prob_Arr.shape[0],1))
    label_result[np.nonzero(prob_Arr > 0.5)[0]] = 1.0
    total_error = 0.0
    for i in range(len(label_result)):
        if label_result[i] != testLabelArr[i]:
            total_error += 1
    errorRate = total_error/ len(label_result)
    return  errorRate


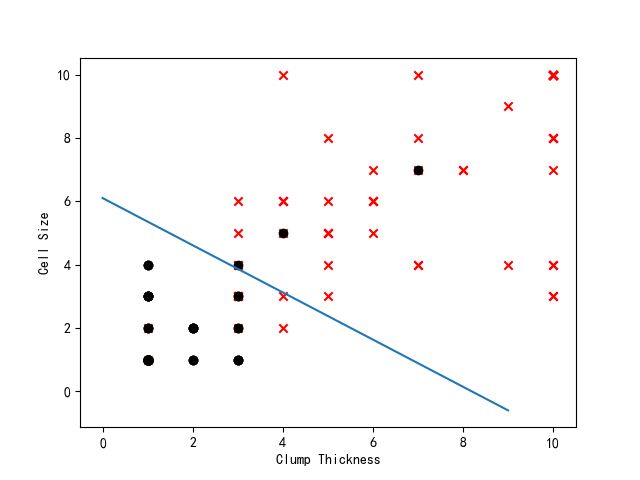
def draw_testDate_scatterGraph(testDateArr, testLabelArr,weight_vector):
    """
    此函数首先将测试数据集按照类别划分为正类和负类两个数据集，然后以散点图的形式将它们展现出来。
    输入： testDateArr 测试数据集（175*2的数组形式）
           testLabelArr 测试数据集对应的类别标签（1*175的数组形式）
    输出： 散点图
    """
    positive_index = np.nonzero( testLabelArr ==1 )
    testDateArr_positive = testDateArr[positive_index]
    negative_index = np.nonzero( testLabelArr == 0 )
    testDateArr_negative = testDateArr[negative_index]
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(testDateArr_positive[:,1], testDateArr_positive[:,2], marker='x', c='red')
    ax.scatter(testDateArr_negative[:, 1], testDateArr_negative[:, 2], marker='o', c='black')
    ax.plot(np.arange(0,10),(-np.arange(0,10)*weight_vector[1]-weight_vector[0])/weight_vector[2])
    plt.xlabel('Clump Thickness', fontsize=10)
    plt.ylabel('Cell Size', fontsize=10)
    plt.show()

接下来，我们编写主函数：

if __name__ == '__main__':
    trainDateArr, trainLabelArr = loadTrainDataSet('breast-cancer-train.csv')
    testDateArr, testLabelArr = loadtestDataSet('breast-cancer-test.csv')
    weight_vector = calculate_regression_coefficient( trainDateArr, trainLabelArr )
    draw_testDate_scatterGraph(testDateArr,testLabelArr,weight_vector)
    errorRate = calculata_errorRate( testDateArr, testLabelArr, weight_vector )
    print('错误率：%f' % errorRate)
    print('正确率：%f' % (1-errorRate))

通过运行，我们得到结果如下：

正确率93%，这已经很不错啦！

至此，我们的 Logistic Regression就学习完毕啦！

参考文献：

[1]   周志华 《机器学习》

[2]   Peter Harrington 《机器学习实战》

本博文为作者原创，作品之著作权属本人所有，未经许可禁止转载。