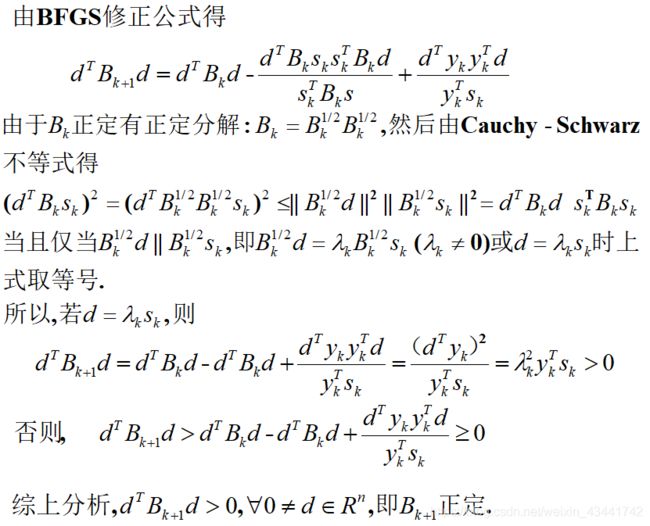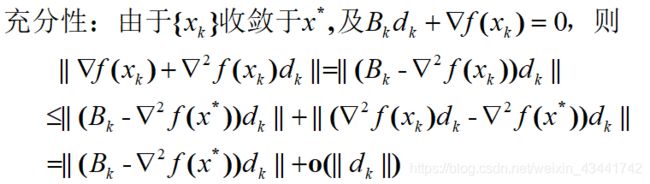深入浅出最优化(4) 拟牛顿法
1 拟牛顿法的数学基础
对于牛顿法,我们保留其快速收敛性,同时克服牛顿法黑森矩阵需要正定的问题以及避免计算黑森矩阵以减少计算量,我们提出了拟牛顿法。
假定当前点为 x k + 1 x_{k+1} xk+1,若我们用已得到的 x k , x k + 1 x_k,x_{k+1} xk,xk+1及其一阶导数信息 g k , g k + 1 g_k,g_{k+1} gk,gk+1,构造一个正定矩阵 B k + 1 B_{k+1} Bk+1作为 G k + 1 G_{k+1} Gk+1的近似。这样根据牛顿法下降方向的产生公式 ∇ 2 f ( x k + 1 ) d k + 1 = − ∇ f ( x k + 1 ) \nabla^2f(x_{k+1})d_{k+1}=-\nabla f(x_{k+1}) ∇2f(xk+1)dk+1=−∇f(xk+1),近似可以得到 B k + 1 d k + 1 = − g k + 1 B_{k+1}d_{k+1}=-g_{k+1} Bk+1dk+1=−gk+1。设 H k + 1 = B k + 1 − 1 H_{k+1}=B_{k+1}^{-1} Hk+1=Bk+1−1,则可以得到 d k + 1 = − H k + 1 g k + 1 d_{k+1}=-H_{k+1}g_{k+1} dk+1=−Hk+1gk+1。
B k + 1 B_{k+1} Bk+1的得出是很理想的,我们希望它能根据已得到的 x k , x k + 1 x_k,x_{k+1} xk,xk+1及其一阶导数信息 g k , g k + 1 g_k,g_{k+1} gk,gk+1用纯迭代的方法得到,而避免黑森矩阵的计算。但想要求得这样的 B k + 1 B_{k+1} Bk+1,首先要知道什么样的 B k + 1 B_{k+1} Bk+1可以作为 G k + 1 G_{k+1} Gk+1的近似矩阵。这个限制条件是保证 x k x_k xk与 x k + 1 x_{k+1} xk+1满足梯度的割线方程。我们知道目标函数梯度函数上两点间的割线方程为 ∇ f ( x k ) − ∇ f ( x k + 1 ) = G k + 1 ( x k − x k + 1 ) \nabla f(x_k)-\nabla f(x_{k+1})=G_{k+1}(x_k-x_{k+1}) ∇f(xk)−∇f(xk+1)=Gk+1(xk−xk+1),那么作为近似的 B k + 1 B_{k+1} Bk+1也必须使得这个方程成立,即 ∇ f ( x k ) − ∇ f ( x k + 1 ) = B k + 1 ( x k − x k + 1 ) \nabla f(x_k)-\nabla f(x_{k+1})=B_{k+1}(x_k-x_{k+1}) ∇f(xk)−∇f(xk+1)=Bk+1(xk−xk+1)。
记 y k = ∇ f ( x k ) − ∇ f ( x k + 1 ) y_k=\nabla f(x_k)-\nabla f(x_{k+1}) yk=∇f(xk)−∇f(xk+1), s k = x k − x k + 1 s_k=x_k-x_{k+1} sk=xk−xk+1,则有拟牛顿方程 B k + 1 s k = y k B_{k+1}s_k=y_k Bk+1sk=yk和第二拟牛顿方程 s k = H k + 1 y k s_k=H_{k+1}y_k sk=Hk+1yk。
2 B k + 1 B_{k+1} Bk+1的计算方法
2.1 BFGS修正公式
给定初始正定矩阵 B 0 B_0 B0,之后有 B k + 1 = B k + Δ k B_{k+1}=B_k+\Delta_k Bk+1=Bk+Δk,假设 Δ k \Delta_k Δk是秩为2的矩阵,则根据矩阵分解有 Δ k = a k u k u k T + b k v k v k T \Delta_k=a_ku_ku_k^T+b_kv_kv_k^T Δk=akukukT+bkvkvkT,其中 a k , b k a_k,b_k ak,bk是任意常数, u k , v k u_k,v_k uk,vk是任意向量,则 B k + 1 = B k + a k u k u k T + b k u k u k T B_{k+1}=B_k+a_ku_ku_k^T+b_ku_ku_k^T Bk+1=Bk+akukukT+bkukukT,代入拟牛顿方程得到 a k u k u k T s k + b k u k u k T s k = y k − B k s k a_ku_ku_k^Ts_k+b_ku_ku_k^Ts_k=y_k-B_ks_k akukukTsk+bkukukTsk=yk−Bksk。不妨设 u k = y k , v k = B k s k u_k=y_k,v_k=B_ks_k uk=yk,vk=Bksk,则 a k = 1 u k T s k = 1 y k T s k , b k = 1 v k T s k = − 1 s k T B k s k a_k=\frac{1}{u_k^Ts_k}=\frac{1}{y_k^Ts_k},b_k=\frac{1}{v_k^Ts_k}=-\frac{1}{s_k^TB_ks_k} ak=ukTsk1=ykTsk1,bk=vkTsk1=−skTBksk1。得到BFGS修正公式:
B k + 1 = B k − B k s k s k T B k s k T B k s k + y k y k T y k T s k B_{k+1}=B_k-\frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k}+\frac{y_ky_k^T}{y_k^Ts_k} Bk+1=Bk−skTBkskBkskskTBk+ykTskykykT
这个公式可以保证每步产生的 B k B_k Bk的正定。(证明见附录1)
2.2 DFP修正公式
H k = B k − 1 H_k=B_k^{-1} Hk=Bk−1,有根据第二你牛顿方程 s k = H k + 1 y k s_k=H_{k+1}y_k sk=Hk+1yk,和BFGS公式使用同样方法推导可得: H k + 1 = H k − H k y k y k T H k y k T H k y k + s k s k T s k T y k H_{k+1}=H_k-\frac{H_ky_ky_k^TH_k}{y_k^TH_ky_k}+\frac{s_ks_k^T}{s_k^Ty_k} Hk+1=Hk−ykTHkykHkykykTHk+skTykskskT
3 拟牛顿法的步骤
- 给定初始点 x 0 ∈ R n x_0\in R^n x0∈Rn, B 0 B_0 B0或 H 0 H_0 H0,精度 ϵ > 0 \epsilon>0 ϵ>0,令 k = 0 k=0 k=0
- 若满足终止准则,则得解 x k x_k xk,算法终止
- 解线性方程组 B k d k + ∇ f ( x k ) = 0 B_k d_k+\nabla f(x_k)=0 Bkdk+∇f(xk)=0,得解 d k d_k dk,或计算 d k = − H k g k d_k=-H_kg_k dk=−Hkgk
- 由线性搜索计算步长 α k \alpha_k αk,令 x k + 1 = x k + α k d k x_{k+1}=x_k+\alpha_kd_k xk+1=xk+αkdk
- 用修正公式得到 B k + 1 B_{k+1} Bk+1或 H k + 1 H_{k+1} Hk+1,使其满足拟牛顿方程, k = k + 1 k=k+1 k=k+1,转2
4 性能评估
- 收敛性:因为保证了 B k B_k Bk正定,则根据古典牛顿法的条件,每一步均会产生下降方向,所以满足收敛性
- 收敛速度:若在最优解处梯度为0、黑森矩阵正定,则当且仅当 lim k → ∞ ∣ ∣ ( B k − ∇ 2 f ( x ∗ ) ) ∣ ∣ ∣ ∣ d k ∣ ∣ = 0 \displaystyle\lim_{k→∞}\frac{||(B_k-\nabla^2f(x^*))||}{||d_k||}=0 k→∞lim∣∣dk∣∣∣∣(Bk−∇2f(x∗))∣∣=0时,算法超线性收敛。(证明见附录2)
- 二次终止性:显然满足,而且因为无需步长搜索,每步步长为1,对于二次函数可以一次取到最优解
- 计算量:小,只需计算两点梯度即可
- 储存空间:大,对于n元目标函数,需要储存一个大小为n*n的矩阵
5 实战测试
对于第一节中提出的最小二乘问题, x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4的初值均在 [ − 2 , 2 ] [-2,2] [−2,2]的范围内随机生成,总共生成100组起点。统计迭代成功(在1000步内得到最优解且单次步长搜索迭代次数不超过1000次)的样本的平均迭代步数、平均迭代时间和得到的最优解及残差平方和最小值。
BFGS:
| 平均迭代步数 | 平均迭代时间 | 最优解 | 残差平方和最小值 |
|---|---|---|---|
| 18.1 | 0.28s | x 1 = 0.1891 x 2 = 0.2820 x 3 = 0.1463 x 4 = 0.1744 x_1=0.1891~x_2=0.2820~x_3=0.1463~ x_4=0.1744 x1=0.1891 x2=0.2820 x3=0.1463 x4=0.1744 | 1.5939 × 1 0 − 4 1.5939\times10^{-4} 1.5939×10−4 |
DFP:
| 平均迭代步数 | 平均迭代时间 | 最优解 | 残差平方和最小值 |
|---|---|---|---|
| 102.05 | 1.86s | x 1 = 0.1689 x 2 = 1.0273 x 3 = 0.3685 x 4 = 0.4585 x_1=0.1689~x_2=1.0273~x_3=0.3685~ x_4=0.4585 x1=0.1689 x2=1.0273 x3=0.3685 x4=0.4585 | 2.6031 × 1 0 − 4 2.6031\times10^{-4} 2.6031×10−4 |
代码实现
BFGS:
import numpy as np
from Function import Function #定义法求导工具
from lagb import * #线性代数工具库
from scipy import linalg
n=4 #x的长度
def myFunc(x):
return #目标方程
k=0
x=np.zeros(n) #初始值点
e=0.001
sigma=0.4
rho=0.55
beta=1
tar=Function(myFunc)
B=np.array(np.eye(n))
while tar.norm(x)>e:
a=1
d=-np.linalg.solve(B,tar.grad(x))
if not (tar.value(x+a*d)<=tar.value(x)+rho*a*dot(turn(tar.grad(x)),d) and \
dot(turn(tar.grad(x+a*d)),d)>=sigma*dot(turn(tar.grad(x)),d)):
a=beta
while tar.value(x+a*d)>tar.value(x)+rho*a*dot(turn(tar.grad(x)),d):
a*=rho
while dot(turn(tar.grad(x+a*d)),d)<sigma*dot(turn(tar.grad(x)),d):
a1=a/rho
da=a1-a
while tar.value(x+(a+da)*d)>tar.value(x)+rho*(a+da)*dot(turn(tar.grad(x)),d):
da*=rho
a+=da
x1=x+a*d
if tar.norm(x1)<e:
print(k+1)
x=x1
break
s=x-x1
y=tar.grad(x)-tar.grad(x1)
B=B-muldot(B,s,turn(s),B)/muldot(turn(s),B,s)+dot(y,turn(y))/dot(turn(y),s)
x=x1
k+=1
print(k)
DFP:
import numpy as np
from Function import Function #定义法求导工具
from lagb import * #线性代数工具库
from scipy import linalg
n=4 #x的长度
def myFunc(x):
return #目标方程
k=0
x=np.zeros(n) #初始值点
e=0.001
sigma=0.4
rho=0.55
beta=1
tar=Function(myFunc)
H=np.array(np.eye(n))
while tar.norm(x)>e:
a=1
d=-dot(H,tar.grad(x))
if not (tar.value(x+a*d)<=tar.value(x)+rho*a*dot(turn(tar.grad(x)),d) and \
dot(turn(tar.grad(x+a*d)),d)>=sigma*dot(turn(tar.grad(x)),d)):
a=beta
while tar.value(x+a*d)>tar.value(x)+rho*a*dot(turn(tar.grad(x)),d):
a*=rho
while dot(turn(tar.grad(x+a*d)),d)<sigma*dot(turn(tar.grad(x)),d):
a1=a/rho
da=a1-a
while tar.value(x+(a+da)*d)>tar.value(x)+rho*(a+da)*dot(turn(tar.grad(x)),d):
da*=rho
a+=da
x1=x+a*d
if tar.norm(x1)<e:
print(k+1)
x=x1
break
s=x-x1
y=tar.grad(x)-tar.grad(x1)
H=H-muldot(H,y,turn(y),H)/muldot(turn(y),H,y)+dot(s,turn(s))/dot(turn(s),y)
x=x1
k+=1
print(k)