数模(5):Malthus和Logistic模型
Malthus拟合和Logistic拟合是两种最典型、应用最广泛的拟合模型。它们分别被用于预测人口增长和物种增长,因此被广泛应用于社会学与生物学领域。
Malthus拟合
通常情况下,每年的人口死亡率与出生率是相同的。因此可以设每年的人口增长率为常数,我们记时刻t的人口数目为x(t),记初始时刻的人口数目为 x 0 x_0 x0,则有:
$
\begin{cases}
\frac{dx}{dt}=rx(t)\
x(0)=x_0
\end{cases}
$
解微分方程可得 x ( t ) = x 0 e r t x(t)=x_0e^{rt} x(t)=x0ert,因此只要确定r的值即可利用Malthus模型拟合数据。
实例
如表给出的近两个世纪美国人口统计数据(以百万为单位),用Malthus模型拟合,并用它预报2010年的美国人口:
| 年份 | 1790 | 1800 | 1810 | 1820 | 1830 | 1840 | 1850 | 1860 | 1870 | 1880 | 1890 | 1900 | 1910 | 1920 | 1930 | 1940 | 1950 | 1960 | 1970 | 1980 | 1990 | 2000 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 人口/百万 | 3.9 | 5.3 | 7.2 | 9.6 | 12.9 | 17.1 | 23.2 | 31.4 | 38.6 | 50.2 | 62.9 | 76.0 | 92.0 | 106.5 | 123.2 | 131.7 | 150.7 | 179.3 | 204.0 | 226.5 | 251.4 | 281.4 |
python代码如下:
import numpy as np
from scipy import optimize
from matplotlib import pyplot
x0=3.9
def f(t,r):
return x0*np.exp(r*t)
x=np.array([3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4
])
t=np.arange(0,220,10)
fita,fitb=optimize.curve_fit(f,t,x,[0],maxfev=5000000)
pyplot.plot(t,x,'.')
x=f(t,fita[0])
pyplot.plot(t,x)
pyplot.show()
print(f(220,fita[0]))
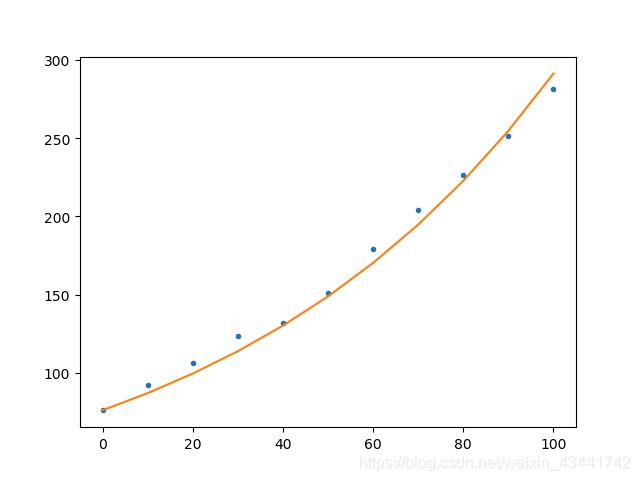
预测结果为413.1,函数图像如下所示:

我们发现,函数并没有很好地拟合,这是因为我们在建立模型时假设的是人口增长率恒定不变。然而实际情况下,随着社会因素的变化,人口增长率是会出现变化的。我们应该选取近期的数据来作为衡量标准计算人口增长率,这将会使得我们对人口的预测变得更加精确。
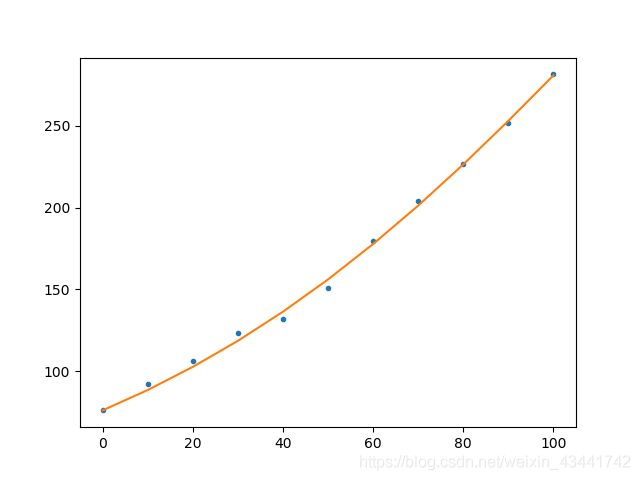
使用1900年后的数据进行拟合,修改python代码如下:
import numpy as np
from scipy import optimize
from matplotlib import pyplot
x0=76.0
def f(t,r):
return x0*np.exp(r*t)
x=np.array([76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4
])
t=np.arange(0,110,10)
fita,fitb=optimize.curve_fit(f,t,x,[0],maxfev=5000000)
pyplot.plot(t,x,'.')
x=f(t,fita[0])
pyplot.plot(t,x)
pyplot.show()
print(f(110,fita[0]))
可以看到此时的拟合效果较好
Logistic拟合
在自然条件下考查一个种群的个体数目变化规律,由于自然条件的限制,个体数目的增长率r应该是一个和个体数目k负相关的函数。对于一个种群来说环境的最大容纳量被称为K值,达到K值之后个体数目便不再增长。我们不妨设增长率r满足方程 r = r 0 ( 1 − x K ) r=r_0(1-\frac{x}{K}) r=r0(1−Kx),记初始时刻的个体数目为 x 0 x_0 x0,则有:
$
\begin{cases}
\frac{dx}{dt}=r_0(1-\frac{x}{K})x\
x(0)=x_0
\end{cases}
$
解微分方程可得 x ( t ) = K 1 + ( K x 0 − 1 ) e − r t x(t)=\frac{K}{1+(\frac{K}{x_0}-1)e^{-rt}} x(t)=1+(x0K−1)e−rtK,这就是Logistic模型,通过拟合确定系数K和r即可使用该模型预测自然条件下的种群个体数目变化情况。
实例
依然以美国人口为例,使用Logistic模型来拟合1900年后的人口数据。python代码如下所示:
import numpy as np
from scipy import optimize
from matplotlib import pyplot
x0=76.0
def f(t,r,K):
return K/(1+(K/x0-1)*np.exp(-r*t))
x=np.array([76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4
])
t=np.arange(0,110,10)
fita,fitb=optimize.curve_fit(f,t,x,[0,400],maxfev=5000000)
pyplot.plot(t,x,'.')
x=f(t,fita[0],fita[1])
pyplot.plot(t,x)
pyplot.show()
print(f(110,fita[0],fita[1]))