算法导论 第二十五章 所有节点对的最短路径问题
基于单源最短路径问题的讨论,解决所有最短路径问题,对每个节点求其最短路径:
25.1 最短路径和矩阵乘法
用动态规划的方法来实现之前的思路:
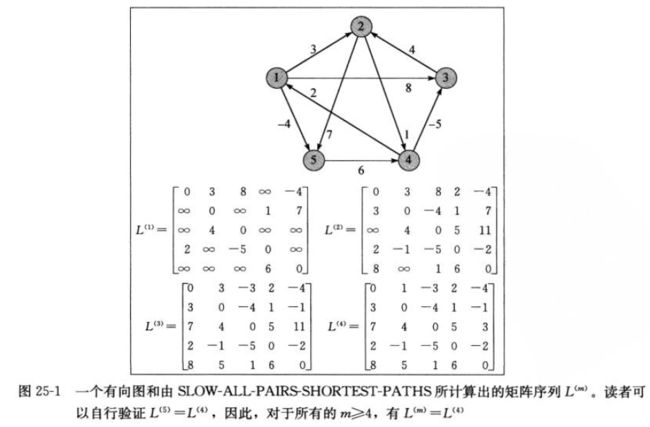
如下示例:
使用公式L[i][j] = min(L[i][j], L'[i][k] + W[k][j])求解第一行的过程如下:
i = 1, j = 1
l'(1,1)= inf; l(1,1) + w(1,1) = 0; l(1,2) + w(2,1) = inf;
l(1,3) + w(3,1) = inf; l(1,4) + w(4,1) = inf; l(5,1) + w(5,1) = inf;
=> l'(1,1) = 0
i = 1, j = 2
l'(1,2)= inf; l(1,1) + w(1,2) = 3; l(1,2) + w(2,2) = 3;
l(1,3) + w(3,2) = 12; l(1,4) + w(4,2) = inf; l(5,1) + w(5,2) = inf;
=> l'(1,2) = 3
i = 1, j = 3
l'(1,3)= inf; l(1,1) + w(1,3) = 8; l(1,2) + w(2,3) = inf;
l(1,3) + w(3,3) = 8; l(1,4) + w(4,3) = inf; l(5,1) + w(5,3) = inf;
=> l'(1,3) = 8
i = 1, j = 4
l'(1,4)= inf; l(1,1) + w(1,4) = inf; l(1,2) + w(2,4) = 4;
l(1,3) + w(3,4) = inf; l(1,4) + w(4,4) = inf; l(5,1) + w(5,4) = 2;
=> l'(1,3) = 2
i = 1, j = 5
l'(1,5)= inf; l(1,1) + w(1,5) = -4; l(1,2) + w(2,5) = 10;
l(1,3) + w(3,5) = inf; l(1,4) + w(4,5) = inf; l(5,1) + w(5,5) = -4;
=> l'(1,5) = -4在形式上转化为
并发现结合律在求min中同样起作用,借用矩阵冥的求解优化来求最短路径:
以上实现和优化的代码实现如下:
def PRINT_GRAPH_MATRIX(G):
format_str = "%-8.2f" * len(G)
for row in G:
print(format_str % tuple(row))
def CREATE_GRAPH_MATRIX(n, val = None):
g = [[val for i in range(n)] for j in range(n)]
return g
def COPY_GRAPH_MATRIX(G):
n = len(G)
g = CREATE_GRAPH_MATRIX(n)
for i in range(n):
for j in range(n):
g[i][j] = G[i][j]
return g
def GRAPH_CONNECT(G, i, j, weight):
G[i-1][j-1] = weight
def EXTEND_SHORTEST_PATHS(L, W):
n = len(L)
rL = CREATE_GRAPH_MATRIX(n, float("inf"))
for i in range(n):
for j in range(n):
for k in range(n):
#print(i, j, k, rL[i][j], L[i][k], W[k][j])
rL[i][j] = min(rL[i][j], L[i][k] + W[k][j])
#print(rL[i][j])
#print("-------------")
return rL
def SLOW_ALL_PAIRS_SHORTEST_PATHS(W):
n = len(W)
L = COPY_GRAPH_MATRIX(W)
for m in range(1, n):
L = EXTEND_SHORTEST_PATHS(L, W)
#PRINT_GRAPH_MATRIX(L)
#print("=================")
return L
def FASTER_ALL_PAIRS_SHORTEST_PATHS(W):
n = len(W)
L = COPY_GRAPH_MATRIX(W)
m = 1
while m < n:
L = EXTEND_SHORTEST_PATHS(L, L)
m = 2*m
return L
if __name__ == "__main__":
G = CREATE_GRAPH_MATRIX(5, float("inf"))
GRAPH_CONNECT(G, 1, 1, 0)
GRAPH_CONNECT(G, 2, 2, 0)
GRAPH_CONNECT(G, 3, 3, 0)
GRAPH_CONNECT(G, 4, 4, 0)
GRAPH_CONNECT(G, 5, 5, 0)
GRAPH_CONNECT(G, 1, 2, 3)
GRAPH_CONNECT(G, 1, 3, 8)
GRAPH_CONNECT(G, 1, 5, -4)
GRAPH_CONNECT(G, 2, 4, 1)
GRAPH_CONNECT(G, 2, 5, 7)
GRAPH_CONNECT(G, 3, 2, 4)
GRAPH_CONNECT(G, 4, 1, 2)
GRAPH_CONNECT(G, 4, 3, -5)
GRAPH_CONNECT(G, 5, 4, 6)
PRINT_GRAPH_MATRIX(G)
print("====================")
L = SLOW_ALL_PAIRS_SHORTEST_PATHS(G)
PRINT_GRAPH_MATRIX(L)
print("====================")
L = FASTER_ALL_PAIRS_SHORTEST_PATHS(G)
PRINT_GRAPH_MATRIX(L)
显而易见算法效率分别为theta(n^4)和theta(n^3lgn).
25.2 Floyd-Warshall 算法
依然是动态规划,但是对于最优解结构的不同处理会导致不同的结果:
其实思路就是看看经过每个节点,看看是否对最短路径是否有改善。实现如下:
def PRINT_GRAPH_MATRIX(G):
format_str = "%-8.2f" * len(G)
for row in G:
print(format_str % tuple(row))
def CREATE_GRAPH_MATRIX(n, val = None):
g = [[val for i in range(n)] for j in range(n)]
return g
def COPY_GRAPH_MATRIX(G):
n = len(G)
g = CREATE_GRAPH_MATRIX(n)
for i in range(n):
for j in range(n):
g[i][j] = G[i][j]
return g
def GRAPH_CONNECT(G, i, j, weight):
G[i-1][j-1] = weight
def INIT_PI_FORM_WEIGHT(W):
n = len(W)
pi = CREATE_GRAPH_MATRIX(n)
for i in range(n):
for j in range(n):
if i == j:
continue
elif W[i][j] != float("inf"):
pi[i][j] = i
return pi
def FLOYD_WARSHALL(W):
n = len(W)
D1 = COPY_GRAPH_MATRIX(W)
P1 = INIT_PI_FORM_WEIGHT(W)
for k in range(n):
D2 = CREATE_GRAPH_MATRIX(n)
P2 = CREATE_GRAPH_MATRIX(n)
for i in range(n):
for j in range(n):
if D1[i][j] <= D1[i][k] + D1[k][j]:
P2[i][j] = P1[i][j]
D2[i][j] = D1[i][j]
else:
P2[i][j] = P1[k][j]
D2[i][j] = D1[i][k] + D1[k][j]
D1 = D2
P1 = P2
return D1, P1
if __name__ == "__main__":
G = CREATE_GRAPH_MATRIX(5, float("inf"))
GRAPH_CONNECT(G, 1, 1, 0)
GRAPH_CONNECT(G, 2, 2, 0)
GRAPH_CONNECT(G, 3, 3, 0)
GRAPH_CONNECT(G, 4, 4, 0)
GRAPH_CONNECT(G, 5, 5, 0)
GRAPH_CONNECT(G, 1, 2, 3)
GRAPH_CONNECT(G, 1, 3, 8)
GRAPH_CONNECT(G, 1, 5, -4)
GRAPH_CONNECT(G, 2, 4, 1)
GRAPH_CONNECT(G, 2, 5, 7)
GRAPH_CONNECT(G, 3, 2, 4)
GRAPH_CONNECT(G, 4, 1, 2)
GRAPH_CONNECT(G, 4, 3, -5)
GRAPH_CONNECT(G, 5, 4, 6)
PRINT_GRAPH_MATRIX(G)
print("====================")
P = INIT_PI_FORM_WEIGHT(G)
print(P)
print("====================")
G,P = FLOYD_WARSHALL(G)
print(P)
print("====================")
PRINT_GRAPH_MATRIX(G)
print("====================")
25.3 用于稀疏图的Johnson算法
算法实现如下:
def PARENT(i):
return (i-1) // 2
def LEFT(i):
return i*2 + 1
def RIGHT(i):
return i*2 + 2
def MIN_HEAPIFY(A, i, size):
l = LEFT(i)
r = RIGHT(i)
if l < size and A[l] < A[i]:
largest = l
else:
largest = i
if r < size and A[r] < A[largest]:
largest = r
if largest != i:
temp = A[i]
A[i] = A[largest]
A[largest] = temp
MIN_HEAPIFY(A, largest, size)
def BUILD_MIN_HEAP(A):
size = len(A)
for i in range(len(A)//2, -1, -1):
MIN_HEAPIFY(A, i, size)
def HEAP_MINIMUM(A):
return A[0]
def HEAP_EXTRACT_MIN(A, size):
assert(size > 0)
iMIN = A[0]
size = size - 1
A[0] = A[size]
MIN_HEAPIFY(A, 0, size)
return iMIN
def HEAP_DECREASE_KEY(A, i, key):
assert(A[i] == key)
A[i] = key
while i > 0 and PARENT(i) >= 0 and A[PARENT(i)] > A[i]:
temp = A[i]
A[i] = A[PARENT(i)]
A[PARENT(i)] = temp
i = PARENT(i)
def MIN_HEAP_INSERT(A, key):
A.append(float("inf"))
HEAP_DECREASE_KEY(A, len(A)-1, key)
#模拟获取index的功能,假设为常数时间
def HEAP_INDEX(A, size, x):
for i in range(0, size):
if A[i] == x:
return i
#======================================================
WHITE, GRAY, BLACK = (0, 1, 2)
def PRINT_GRAPH_MATRIX(G):
format_str = "%-8.2f" * len(G)
for row in G:
print(format_str % tuple(row))
def CREATE_GRAPH_MATRIX(n, val = None):
g = [[val for i in range(n)] for j in range(n)]
return g
class Vertex:
def __init__(self, u):
self.value = u
self.vertexs = []
self.isInGraph = False
self.pi = None
self.d = float("inf")
self.h = float("inf")
self.color = WHITE
def __lt__(self, u):
return self.d < u.d
class Edge:
def __init__(self, u, v, w):
self.fromV = u
self.toV = v
self.weight = w
class Graph:
def __init__(self):
self.vertexs = []
self.edges = []
def weight(edges, u, v):
for e in edges:
if e.fromV == u and e.toV == v:
return e.weight
print(u.value, v.value)
return None
def INITGRAPH(G, edges):
for e in edges:
if not e.fromV.isInGraph:
G.vertexs.append(e.fromV)
e.fromV.isInGraph = True
if not e.toV.isInGraph:
G.vertexs.append(e.toV)
e.toV.isInGraph = True
G.edges.append(e)
e.fromV.vertexs.append(e.toV)
def INITIALIZE_SINGLE_SOURCE(G, s):
for v in G.vertexs:
v.d = float("inf")
v.pi = None
s.d = 0
s.pi = None
def DIJKSTRA(G, s):
def RELAX(Q, size, u, v, edges):
if v.d > u.d + weight(edges, u, v):
index = HEAP_INDEX(Q, size, v)
v.d = u.d + weight(edges, u, v)
HEAP_DECREASE_KEY(Q, index, v)
v.pi = u
print("relax", u.value, v.value, v.d)
INITIALIZE_SINGLE_SOURCE(G, s)
S = []
Q = []
for v in G.vertexs:
Q.append(v)
size = len(Q)
BUILD_MIN_HEAP(Q)
while size != 0:
u = HEAP_EXTRACT_MIN(Q, size)
size = size - 1
S.append(u)
for v in u.vertexs:
RELAX(Q, size, u, v, G.edges)
def BELLMAN_FORD(G, s):
def RELAX(u, v, edges):
if v.d > u.d + weight(edges, u, v):
v.d = u.d + weight(edges, u, v)
v.pi = u
print(u.value, v.value, v.d)
INITIALIZE_SINGLE_SOURCE(G, s)
for i in range(1, len(G.vertexs)-1):
for edge in G.edges:
RELAX(edge.fromV, edge.toV, G.edges)
for edge in G.edges:
if edge.toV.d > edge.fromV.d + weight(G.edges, edge.fromV, edge.toV):
return False
return True
def INSERT_SOURCE_VERTEX(G):
s = Vertex(0)
for v in G.vertexs:
G.edges.append(Edge(s, v, 0))
s.vertexs.append(v)
s.isInGraph = True
G.vertexs.append(s)
return s
def CREATE_NEW_WEIGHT_GRAPH(G):
new_edges = []
old_edges = G.edges
for v in G.vertexs:
v.h = v.d
for e in old_edges:
w = e.weight + e.fromV.h - e.toV.h
new_edges.append(Edge(e.fromV, e.toV, w))
G.edges = new_edges
return old_edges
def JOHNSON(G):
n = len(G.vertexs)
s = INSERT_SOURCE_VERTEX(G)
if BELLMAN_FORD(G, s):
CREATE_NEW_WEIGHT_GRAPH(G)
D = CREATE_GRAPH_MATRIX(n, float("inf"))
for u in G.vertexs:
if u == s:
continue
DIJKSTRA(G, u)
for v in G.vertexs:
if v == s:
continue
D[u.value-1][v.value-1] = v.d + v.h - u.h
return D
if __name__ == "__main__":
node1 = Vertex(1)
node2 = Vertex(2)
node3 = Vertex(3)
node4 = Vertex(4)
node5 = Vertex(5)
edges = []
edges.append(Edge(node1, node2, 3))
edges.append(Edge(node1, node3, 8))
edges.append(Edge(node1, node5, -4))
edges.append(Edge(node2, node4, 1))
edges.append(Edge(node2, node5, 7))
edges.append(Edge(node3, node2, 4))
edges.append(Edge(node4, node1, 2))
edges.append(Edge(node4, node3, -5))
edges.append(Edge(node5, node4, 6))
G = Graph()
INITGRAPH(G, edges)
D = JOHNSON(G)
PRINT_GRAPH_MATRIX(D)
习题解答