Exploring GLSL – Normal Visualizer with Geometry Shaders

http://www.geeks3d.com/20130905/exploring-glsl-normal-visualizer-with-geometry-shaders-shader-library/

Exploring GLSL – Normal Visualizer with Geometry Shaders (Shader Library)

2013/09/05 JeGX GLSL Hacker, OpenGL, Programming, Shader Library, Tutorial

---

Article index:

• 1 – Vertex Normal Visualizer
• 2 – Face Normal Visualizer
• 3 – References

Hi dear readers, I’m back! Three weeks without new posts… Lot of things to do combined with many sunny days == no post on Geeks3D 

Today, we’re going to see a simple but really useful application of geometry shaders: a normal visualizer. I already talked about GLSL geometry shaders HERE and HERE.

A geometry shader allows to create new geometry (a vertex, a line or a polygon) on the fly. We will use this feature to generate lines for visualizing the normals of both vertices and faces of a triangular mesh.

The demos of this article have been coded with GLSL Hacker and you can find all source codes in the Code Sample Pack under the GLSL_Geometry_Shader_Normal_Visualizer/ folder. You can download GLSL Hacker from this page (I recommend to grab the latest DEV version).

As usual, the GLSL programs are not specific to GLSL Hacker. You can use them in any OpenGL/WebGL application with minor changes only (shader inputs).

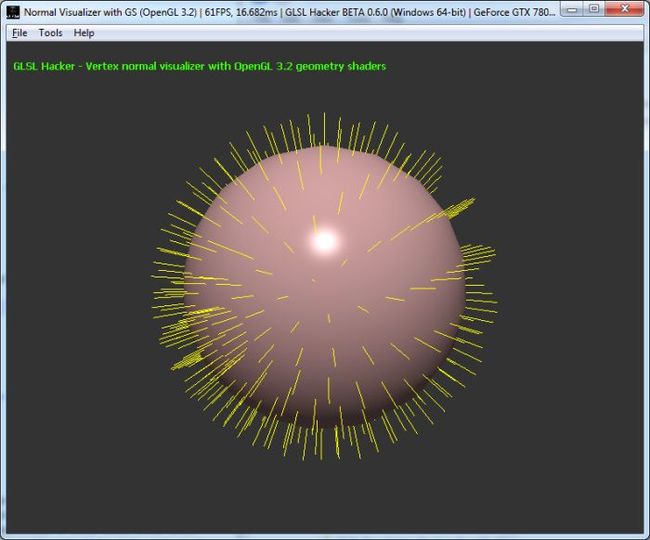
1 – Vertex Normal Visualizer

The generation of the vertex normals is simple. Each normal is a line made up of two vertices. The first vertex is equal to the incoming vertex (which belongs to the current mesh). The second vertex is equal to the first vertex with a displacement along the direction of the vertex normal:

V0 = Pi
V1 = Pi + (normal_length * Ni)

Where i is the vertex index (0 to 2 because the input of the geometry shader is a triangle), Pi and Ni are the position and the normal of the i-th vertex. V0 and V1 are the vertices of the new line.

The vertex normal is part of the geometry shader input vertex. Here is the complete GLSL program (vertex + geometry + fragment) that renders the vertex normals:

Vertex shader
This is a simple pass-trough vertex shader. No transformation here, vertices will be transformed for final display in the geometry shader.

#version 150
in vec4 gxl3d_Position;
in vec4 gxl3d_Normal;

out Vertex
{
  vec4 normal;
  vec4 color;
} vertex;

void main()
{
  gl_Position = gxl3d_Position;
  vertex.normal = gxl3d_Normal;
  vertex.color =  vec4(1.0, 1.0, 0.0, 1.0);
}

Geometry shader
The geometry shader does most of the work: it transforms vertices from local space to window space (gxl3d_ModelViewProjectionMatrix) and creates the lines:

#version 150
layout(triangles) in;

// Three lines will be generated: 6 vertices
layout(line_strip, max_vertices=6) out;

uniform float normal_length;
uniform mat4 gxl3d_ModelViewProjectionMatrix;

in Vertex
{
  vec4 normal;
  vec4 color;
} vertex[];

out vec4 vertex_color;

void main()
{
  int i;
  for(i=0; i 
   
Fragment shader
 
   
#version 150
in vec4 vertex_color;
out vec4 Out_Color;
void main()
{
  Out_Color = vertex_color;
}
 
   
 
   
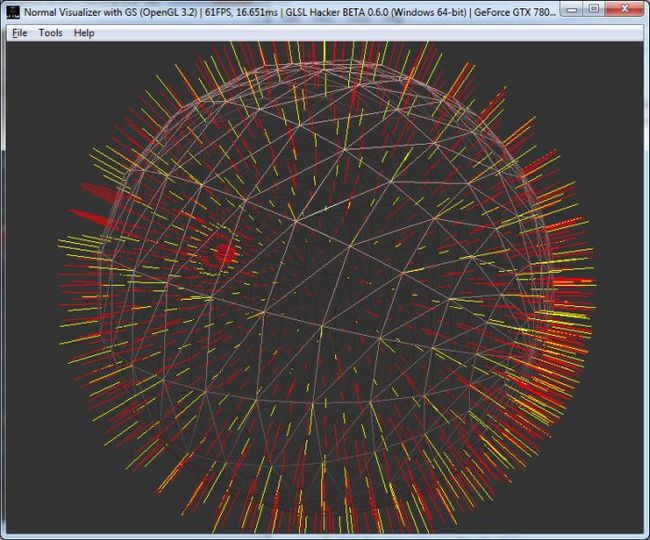
2 – Face Normal Visualizer
 
    
    
 
    
   
The generation of the vertex normal was simple. Let’s see now how to generate the face normal in the geometry shader. All we need are the thee vertices that define a triangle. We are lucky because those vertices are the inputs of the geometry shader thanks to the following line:
 
   
layout(triangles) in; 
 
   
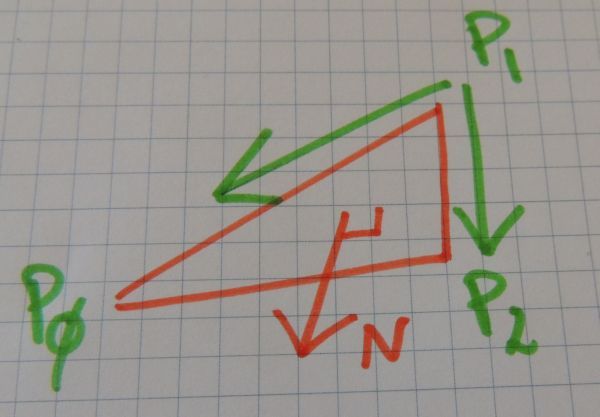
If P0, P1 and P2 are the positions of the face vertices, the face normal is the result of the following cross product:
 
   
V0 = P0-P1
V1 = P2-P1
N = cross (V1, V0)
 
    
    
 
    
   
We have now all the theory we need to code the face normal visualizer. Here is the code of the geometry shader alone because compared to the previous GLSL program, only the geometry shader is updated. This geometry shader generates 3 lines for the vertex normals (in yellow) and one line for the face normal (in red): 4 lines or  8 vertices.
 
   
Geometry shader
 
   
#version 150
layout(triangles) in;
layout(line_strip, max_vertices=8) out;

uniform float normal_length;
uniform mat4 gxl3d_ModelViewProjectionMatrix;

in Vertex
{
  vec4 normal;
  vec4 color;
} vertex[];

out vec4 vertex_color;

void main()
{
  int i;
  
  //------ 3 lines for the 3 vertex normals
  //
  for(i=0; i 
   
 
   
3 – References
 
   
 
    
OpenGL Superbible, fifth edition, chapter 11
 
   
 
    
    
 
    
 
    
 
    
   
 
   
 
   
 
    
 
    
Related posts:
 
    
 
     
Mesh Exploder with Geometry Shaders 
 
     
Simple Introduction to Geometry Shaders in GLSL (Part 2) 
 
     
Particle Billboarding with the Geometry Shader (GLSL) 
 
     
(Shader Library) Bumpy Sphere Env Normal Mapping 
 
     
Simple Introduction to Geometry Shaders in GLSL (Part 1) 
 
    
 
   
 
  

geometry shader, glsl, glslhacker, normal, opengl, shader library, tutorial, visualizer