26、图算法-最小生成树、最短路径

1、带权图，每个边附带一个值或权
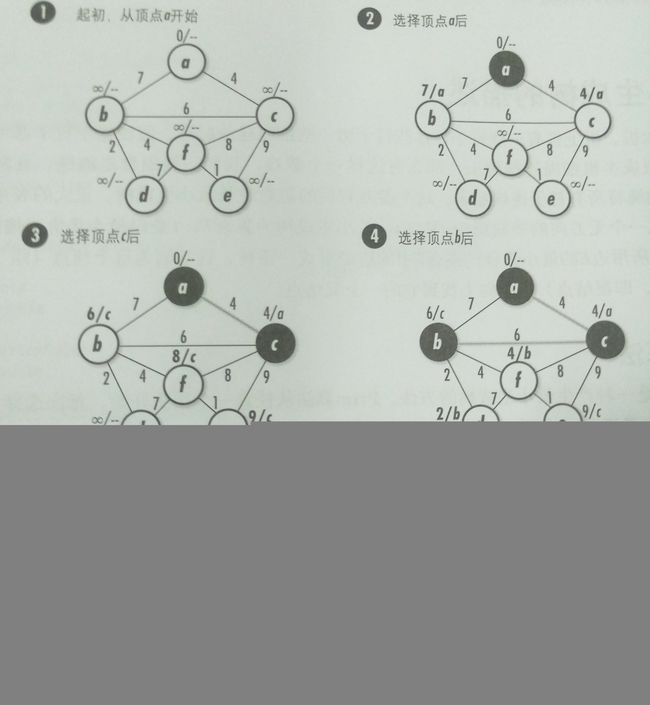
（1）最小生成树：以最小代价将一个无方向的带权图的所有节点连起来，除根节点外，每个节点都有一个父节点所以叫最小生成树。
（2）最短路径：连接一个有方向的带权图中两个顶点之间代价的最小距离
（3）旅行商问题：寻找能够遍历一个完整且无方向带权图中每个顶点（仅一次），并且最终返回到起始顶点的路径。

2、最小生成树Prim算法

起始：把所有节点键值置为无穷大，根节点置为0。右边填上父节点，左边是到自己的键值

3、最小生成树代码
（1）数据结构

//MstVertex是AdjList中vertex指向的内容，原树节点data指向AdjList
//weight：达到该顶点的边的权值，不常使用只有储存到邻接表中时才用到，一般操作 key
//key：键值

typedef struct MstVertex_
{
    void *data;
    double weight;

    VertexColor color;
    double key;
    struct MstVertex_ *parent;
}MstVertex;

typedef struct AdjList_{
    void *vertex;
    SET_ARRT adjacent;
}AdjList;

（2）实现

//start:指明开头点
//span：返回生成的最小生成树 
int mst(Graph *graph, const MstVertex *start, LIST_ATTRITIVE *span, int (*match)(const void *key1, const void *key2))
{
    AdjList *adjlist;
    MstVertex *mst_vertex, *adj_vertex;
    LIST_ELEMENT *elememt, *member;
    double minimum;
    int found, i;

    //找到开头节点，把该节点的key设为0，其他设为无穷大 
    found = 0;
    for(element = list_head(graph->adjlists); element != NULL; element = list_next(element))
    {
        mst_vertex = ( (AdjList *)(list_data(element)) )->vertex;

        if(match(mst_vertex, start))
        {
            mst_vertex->color = white;
            mst_vertex->key = 0;
            mst_vertex->parent = NULL;
            found = 1;
        }
        else
        {
            mst_vertex->color = white;
            mst_vertex->key = DBL_MAX;
            mst_vertex->parent = NULL;
        }
    }
    if(!found)
        return -1;

    //遍历所有节点，每次涂一个节点 
    i = 0;
    while(i < graph->vcount)
    {
        minimum =  DBL_MAX;

        //每次找到没涂黑的节点中 key 最小的点 
        for(element = list_head(graph->adjlists); element != NULL; element = list_next(element))
        {
            mst_vertex = ( (AdjList *)(list_data(element)) )->vertex;
            if(mst_vertex->color == white && mst_vertex->key < minimum)
            {
                minimum = mst_vertex->key;
                adjlist = list_data(elememt); 
            }
        }
        ((MstVertex *)adjlist->vertex)->color = black;//找到这次最小的点涂黑 


        //遍历本次最小节点的邻接点，如果它在前面已经改过key 和parent，
        //并且它为白色，和本次相连key更小就需要修改key 和parent 
        for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(element))
        {
            adj_vertex = list_data(member);
            for(element = list_head(graph->adjlists); element != NULL; element = list_next(element))
            {
                    mst_vertex = ( (AdjList *)(list_data(element)) )->vertex;
                    if(match(mst_vertex, adj_vertex))
                    {
                        if(mst_vertex->color == white && adj_vertex < mst_vertex->key)
                        {
                            mst_vertex->key = adj_vertex->key;
                            mst_vertex->parent = adj_vertex->parent;
                        }
                        break;
                    }
            }
        }
        i++;

        //每次涂黑一个，每次放一个到树中 
        list_init(span, NULL);
        for(element = list_head(graph->adjlists); element != NULL; element = list_next(element))
        {
            mst_vertex = ( (AdjList *)(list_data(element)) )->vertex;
            if(mst_vertex->color == black)
                //不会插入已经存在的
                list_ins_next(span, list_tail(span), mst_vertex);
        } 
    } 
    return 0;
}

4、最短路径Dijkstra算法

以涂黑的点为基准判断之前修改的白色节点知否需要修改，再选择有数据的最小白节点涂黑。
类似最小生成树，区别在于寻找的是最小key，还是最小d
（1） 数据结构

typedef struct PathVertex_
{
    void *data;
    double weight;
    VertexColor color;

//从起点开始到该节点所有key值的和
    double d;
    struct PaPathVertex_ *parent;
}PathVertex;

（2）

//判断v的距离是否需要更新，u视为v的父节点，如果v的距离大于u距离+u到v的权值则更新 
static void relax(PathVertex *u, PathVertex *v, double weight)
{
    if(v->d > u->d + weight)
    {
        v->d = u->d + weight;
        v->parent = u; 
    }
    return;
}


//头结点到任意其他节点之间的路径都是最短路径
// path中保存所有处理后的节点，他们有d值和自己的父节点，虽然无序，但很容易处理 
int shortest(Graph *graph, const PathVertex *start, LIST_ATTRITIVE *path, int (*match)(const void *key1, const void *key2))
{
    AdjList *adjlist;
    PathVertex *pth_vertex, *adj_vertex;

    LIST_ELEMENT *elememt, *member;
    double minimum;
    int found, i;

    //找到开头节点，把该节点的key设为0，其他设为无穷大 
    found = 0;
    for(element = list_head(graph->adjlists); element != NULL; element = list_next(element))
    {
        pth_vertex = ( (AdjList *)(list_data(element)) )->vertex;

        if(match(pth_vertex, start))
        {
            pth_vertex->color = white;
            pth_vertex->d = 0;
            pth_vertex->parent = NULL;
            found = 1;
        }
        else
        {
            pth_vertex->color = white;
            pth_vertex->key = DBL_MAX;
            pth_vertex->parent = NULL;
        }
    }
    if(!found)
        return -1;

    //遍历vcount次，每次涂一个节点 
    i = 0;
    while(i < graph->vcount)
    {
        minimum =  DBL_MAX;

        //每次找到没涂黑的节点(其父节点为黑)中 key 最小的点 
        for(elememt = list_head(graph->adjlists); elememt != NULL; elememt = list_next(elememt))
        {
            pth_vertex = ( (AdjList *)(list_data(elememt)) )->vertex;
            if(pth_vertex->color == white && pth_vertex->d < minimum)
            {
                minimum = pth_vertex->key;
                adjlist = list_data(elememt); 
            }
        }
        ((PathVertex *)adjlist->vertex)->color = black;//找到这次最小的点涂黑 


        //遍历本次最小节点的邻接点，如果它在前面已经改过d和parent，
        //并且它为白色，和本次相连d（父节点的d加边的权值）更小就需要修改d 和parent 
        for(member = list_head(&adjlist->adjacent); member != NULL; member = list_next(elememt))
        {
            //adj_vertex为本次黑色点的一个邻接点（白色） 
            adj_vertex = list_data(member);
            for(elememt = list_head(graph->adjlists); elememt != NULL; elememt = list_next(elememt))
            {
                    //修改所有需要修改的邻接点 
                    pth_vertex = ( (AdjList *)(list_data(elememt)) )->vertex;
                    if(match(pth_vertex, adj_vertex))
                    {   
                        relax(adjlist->vertex, pth_vertex, adj_vertex->weight);
                    }
            }
        }
        i++;

        //每次涂黑一个，每次放一个到树中 
        list_init(path, NULL);
        for(elememt = list_head(graph->adjlists); elememt != NULL; elememt = list_next(elememt))
        {
            pth_vertex = ( (AdjList *)(list_data(elememt)) )->vertex;
            if(pth_vertex->color == black)
                list_ins_next(path, list_tail(path), pth_vertex);
        } 
    } 
    return 0;

}