可持久化数据结构c++

可持久化数据结构的原理在于，每次修改创造一个新节点作为根，对修改部分再创一条链，对于未修改部分直接连向上次修改连向的位置，这样，就可以在较小的空间存储每次修改时的状态.

以可持久化字典树为例

如果我们要加入cat，cap，rat，cute，等词

第一步

然后，再插入第二个单词

可以看到，新建一棵树存当前的词，然后连向之前已经有过的树
第三第四个单词

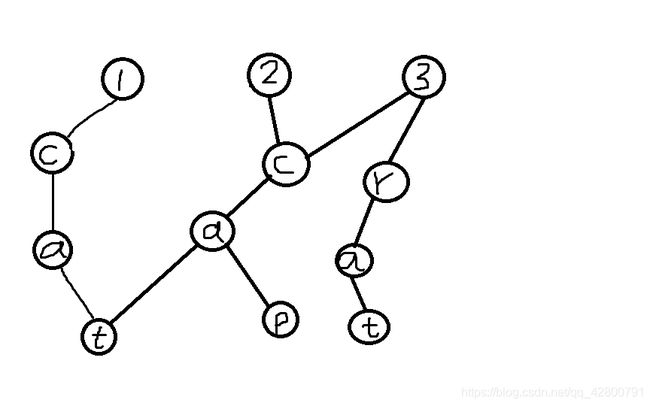
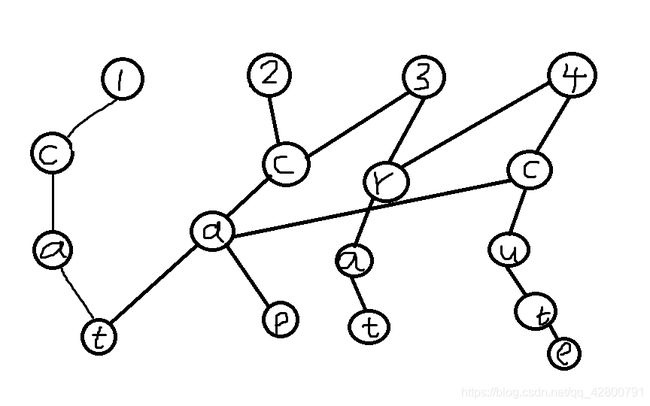
以上就是可持久化字典树的内容

可持久化线段树同理

每次修改添加一条，剩下的直接连向之前的

可持久化字典树 例题

最大异或和（ https://www.luogu.org/problemnew/show/P4735 ） 洛谷P4735

题目详解

每次将前缀和的二进制形式加入到0/1字典树中

询问时优先询问与某关键值（x^s[N]）相反的路径

从高位到低位存储和询问

因为0/1字典树是二叉的，所以连向上一段的已有子树可以直接连接

数组解释

int trie[MAXN*24][2],latest[MAXN*24];//字典树；当前结点向下传递的最后一个前缀和的位置编号
//位置编号就是指插入的顺序编号
int s[MAXN],root[MAXN],N,M,tot;//前缀和；根据更改先后变化的根节点

以下是插入操作

void insert(int i,int k,int p,int q)//第i个前缀和，二进制从低到高第k位，p为上一段同深度端点，q为当前端点
{
	if(k<0) {latest[q]=i;return;}
	int c=s[i]>>k&1;
	if(p) trie[q][c^1]=trie[p][c^1];//如果上一段有平行的对应结点则连接
	trie[q][c]=++tot;//新建结点
	insert(i,k-1,trie[p][c],trie[q][c]);//插入下一个结点
	latest[q]=max(latest[trie[q][0]],latest[trie[q][1]]);//向下最大的末位前缀和位置编号
}

以下是完整代码

#include
#include
#include
#include
#define R Rein()
#define lR lRein()
#define ll long long int
#define ri register int
inline int R{int x=0,f=1;char c=getchar();while(c<'0'||c>'9')if(c=='-') f=-1,c=getchar();else c=getchar();while(c<='9'&&c>='0')x=10*x+c-'0',c=getchar();return f*x;}
inline ll lR{ll x=0,f=1;char c=getchar();while(c<'0'||c>'9')if(c=='-') f=-1,c=getchar();else c=getchar();while(c<='9'&&c>='0')x=10*x+c-'0',c=getchar();return f*x;}
using namespace std;
const int DEVIATION=10;
const int MAXN=3e5+DEVIATION;
int trie[MAXN*24][2],latest[MAXN*24];
int s[MAXN],root[MAXN],N,M,tot;
void insert(int i,int k,int p,int q)
{
	if(k<0) {latest[q]=i;return;}
	int c=s[i]>>k&1;
	if(p) trie[q][c^1]=trie[p][c^1];
	trie[q][c]=++tot;
	insert(i,k-1,trie[p][c],trie[q][c]);
	latest[q]=max(latest[trie[q][0]],latest[trie[q][1]]);
}
int ask(int now,int val,int k,int limit)
{
	if(k<0) return s[latest[now]]^val;
	int c=val>>k&1;
	if(latest[trie[now][c^1]]>=limit)
		return ask(trie[now][c^1],val,k-1,limit);
	else
		return ask(trie[now][c],val,k-1,limit);
}
int main()
{
	N=R,M=R;
	latest[0]=-1;
	root[0]=++tot;
	insert(0,23,0,root[0]);
	for(ri i=1;i<=N;i++)
		s[i]=s[i-1]^R,
		root[i]=++tot,
		insert(i,23,root[i-1],root[i]);
	for(ri i=1;i<=M;i++)
	{
		char op[2];scanf("%s",op);
		if(op[0]=='A')
			root[++N]=++tot,
			s[N]=s[N-1]^R,
			insert(N,23,root[N-1],root[N]);
		else
		{
			int l=R,r=R,x=R;
			printf("%d\n",ask(root[r-1],x^s[N],23,l-1));
		}
	}
	return 0;
}