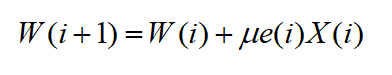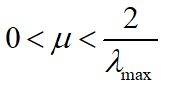【优化】超详细的LMS算法的matlab实现
LMS自适应滤波算法是基于维纳滤波算法，在最陡梯度下降法的基础上形成的滤波算法，它用梯度矢量的估计值来代替其精确值，应用广泛。本文是自己在入门学习LMS算法时整理归纳所得，里面包含了自己在编程实现时的疑问及自我思考后的解答，如有不足，虚心请求请指正。
LMS算法的理论基础
- LMS算法的损失函数（cost function）为：
- LMS算法的递推公式为：
注: μ为调整步长的常数，用于控制系统的稳定性和自适应算法的收敛速度,为下面代码示例中的mu. - LMS算法实现步骤
- 令起始时刻 i=0自适应滤波器的系数矢量W(0)为任意值；
- 根据输入信号矢量X(i) ，利用期望信号d(i) 和滤波器的输出信号 y(i)计算误差信号e(i);
- 根据误差信号，利用以下的递推公式 ，进行滤波器系数的更新；
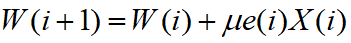
- 重复步骤2）和3），直到达到平稳状态（系数W几乎保持不变）。
-
LMS算法的收敛条件：
通过引入系数误差矢量 ，整理得LMS算法的收敛条件为 ：
注： λmax为输入信号的自相关矩阵 的最大特征值
LMS算法的matlab实现
LMS算法的实现程序分为两个部分，第一部分为LMS算法函数，主要完成LMS的实现过程；第二部分为主函数，用来准备数据和调用第一部分的算法实现滤波。
- LMS子程序
function [w,en,yn] = my_LMS(xn,dn,mu)
%LMS实现程序
% 输入：
% xn 输入信号 列向量
% dn 理想信号 列向量
% mu 收敛常数 标量
% itr 迭代次数 标量
% M 滤波器的阶数 标量
% 输出：
% w 滤波器的系数矩阵 大小为M×itr 每一列代表一次迭代后的系数
% en 误差信号 大小为itr×1 每一行代表一次迭代后产生的误差
% yn 滤波器的输出信号 列向量
M = 30; %定义滤波器的阶数为30
itr = length(xn); %使得迭代次数为输入信号xn的长度
w = zeros(M,itr);%将滤波器的初始值设置为0
en = zeros(itr,1);%将初始误差设置为0
%迭代更新滤波器的参数
for k = M:itr %要保证输入延时后的信号有效，所以实际的迭代次数只有（itr-M）次，
x = xn(k:-1:k-M+1);%将输入信号延迟，使得滤波器的每个抽头都有输入
y = w(:,k-1).'*x; %计算出滤波器的输出
en(k) = dn(k)-y; %得出误差信号
w(:,k) = w(:,k-1)+mu*en(k)*x;%迭代更新滤波器的系数
end
%滤波器参数固定后，得出经过优化滤波器滤波后的输出信号
yn = inf*ones(length(xn));%inf意为无穷大，将yn的初始值置为无穷大，绘制图像的时候将无法显示
for k = M:itr
x = xn(k:-1:k-M+1);
yn(k) = w(:,k).'*x;
end
end
- LMS主程序
%%%% LMS自适应滤波算法实现滤波功能 %%%%
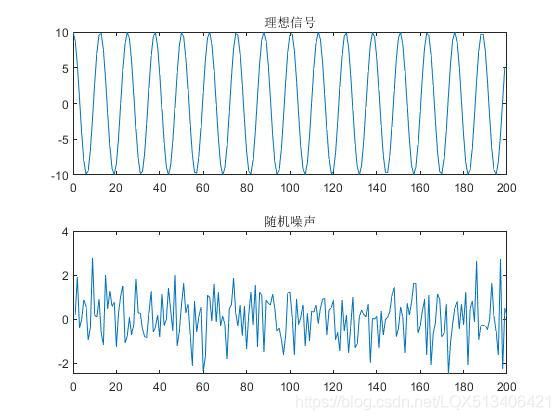
% 产生理想信号
t = 0:199
xs = 10*cos(0.5*t);%xs为理想的余弦信号
%绘制理想信号的图像
figure;
subplot(2,1,1);
grid;%显示窗格
plot(t,xs);
title("理想信号");
%产生随机噪声信号
xn = randn(1,200);%产生一个1×200大小的噪声信号
%绘制随机噪声的图像
subplot(2,1,2);
grid;%显示窗格
plot(xn);
title("随机噪声");
%产生输入信号
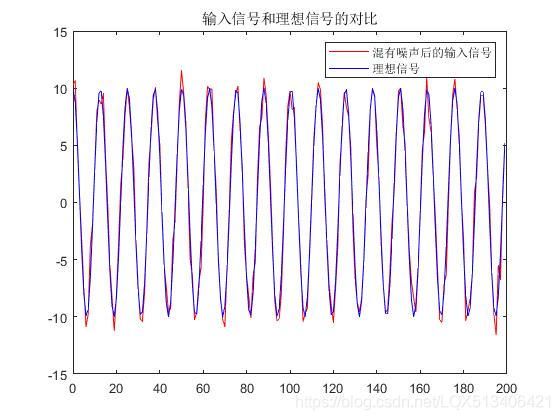
xn = xs+xn;
xn = xn.';%将输入信号由行向量转置为列向量
dn = xs.';%将理想信号由行向量转置为列向量
%绘制输入信号和理想信号的图像
figure;
plot(t,xn,'r',t,dn,'blue');
legend('混有噪声后的输入信号','理想信号');
title('输入信号和理想信号的对比');
%求收敛常数
fe = max(eig(xn*xn.'));%求解输入xn的自相关矩阵的最大特征值fe,A = eig(B),意为将矩阵B的特征值组成向量A
mu = 2*(1/fe);
%引用LMS算法实现滤波
[w,en,yn] = my_LMS(xn,dn,mu);
%绘制滤波器输出信号和误差信号图像
figure;
subplot(2,1,1);
grid;
plot(yn);%绘制经过滤波器滤波后信号
subplot(2,1,2);
grid;
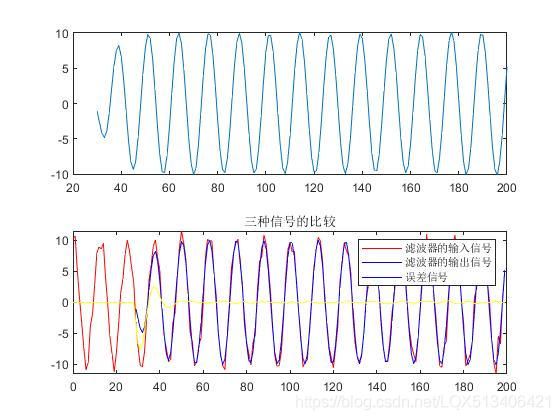
plot(t,xn,'red',t,yn,'blue',t,en,'yellow');
legend('滤波器的输入信号','滤波器的输出信号','误差信号');
title('三种信号的比较');
算法运行结果
学习过程中的问题及解答
- 理想信号d(i)如何获得？
答：要设计一个滤波器，设计者需要知道滤波器的实际输入和理想的输出，不然就谈不上进行滤波器设计。故LMS滤波算法中的理想信号d(i)，即滤波器的理想输出,其实与机器学习中的label有异曲同工之妙，都是人为规定的。d(i)的存在是为了得出滤波器的代价函数（cost function），LMS算法的实质是最小化其代价函数，当代价函数最小时，滤波器的参数就能取得最优值，即滤波器设计完毕。 - LMS子程序中滤波器每个抽头的输入如何获得？
答： 以下图为例子（引用于[1]），滤波器每个抽头的输入都是输入信号x(i)延时的结果，故在LMS程序中用以下语句实现，在本例中，输入信号是一个200×1的列向量，要保证输入的延时信号有效，实际迭代的次数只有170次，故w矩阵30列以前的值都为0，滤波器输出yn列向量30行以前都为无穷大，误差e(i)的30行以前都为0。
for k = M:itr %要保证输入延时后的信号有效，所以实际的迭代次数只有（itr-M）次，
x = xn(k:-1:k-M+1);%将输入信号延迟，使得滤波器的每个抽头都有输入
y = w(:,k-1).'*x; %计算出滤波器的输出
en(k) = dn(k)-y; %得出误差信号
w(:,k) = w(:,k-1)+mu*en(k)*x;%迭代更新滤波器的系数
end
4. 在程序中为什么要把yn的初始值设为无穷大？
答： 在matlab的绘图程序中，由于精度的问题，无法绘制出无穷大，故若将yn的初始值设置为无穷大，绘制其图像时，其前面30行就不会出现在图中，可以便于观察，与之对应的是误差信号en的初始值设置为0，故绘制其图像时，前面无效的30行也出现在图中了，显得有些乱。不过仁者见仁，智者见智，可以自己根据自己的喜好自动调整。
[1]陈文晓. 无线传感器网络中分布式LMS算法的研究[D].西安邮电大学,2014
[2]future_fighter.LMS算法Matlab实现.https://blog.csdn.net/future_fighter/article/details/2334181