神经网络学习笔记(一) 单层感知机
前向网络
神经网络分为从传播来讲分为两种:
1.前馈神经网络(前向网络)
2.反馈神经网络
前向网络没有反馈机制,也就是自能向前传播而不能反向传播来调整权值参数。感知机就属于前向网络。
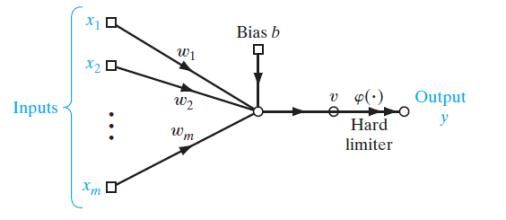
如上图 一个输入层,一个输出层,中间的所有隐层都是向前传播。
感知机
感知机是美国学者F.Rosenblatt提出的,他对最早提出的MP不一样,他的所有维度 的权值是可以改变的,通过对权值的迭代可以快速的解决线性可分的二分类问题。
上面这幅图片就是一个单层感知机示意图,有一个输入层,一个输出层,m个维度的数据通过每个维度权值w和偏置b来得到最终结果。
详解单层感知机
首先我们要了解我们需要解决什么问题。
举个例子:
我有四个平面点(笛卡尔坐标系下) 分别是(0,0) (1,0) (0,1) (1,1)。
现在我想把坐标中带0的坐标点归为一类(类别0),不带0的为另一类(类别1)。
就有如下:
(0,0) (1,0) (0,1)====》》类别0
(1,1)================》》类别1
那么我们要怎样一刀切呢,有很多种切法都能分开,那么怎么让计算机来切? 这时就该单层感知机登场了!!
单层感知机就是在每个维度上乘上一个权值w 并且在最后加上偏置 使输出=预期
也就是每个维度上都有 t(i)=w(i)x(i) 整个式子就是 t=w(1)x(1)+w(2)x(2)+w(n)x(n)+b
t就是我们的目标分类值;
w就是每个维度上的权值;
b就是总体的偏置;
就拿我们的例子来说 假设训练好的权值为 w(1)、w(2) ,偏置为b
在第二个点上有:1*w(1)+0*w(2)+b<0 (我们把<0归为0 大于0归为1 这个函数也称标志函数)
用同样的权值和偏置在第四个点上有1*w(1)+1*w(2)+b>0
这就是单层感知机。
代码编写(Matlab非API实现)
首先我们要写一个标志函数 sgn
这个函数实现了 >0归一 <0归零 的功能
function a = sgn( input )
a=zeros(1,length(input));
for i=1:length(input)
temp=input(i);
if temp>0
a(i)=1;
else
a(i)=0;
end
end
end接下去就是逻辑代码的编写
我们把偏置b当作第三维向量输入
terminalnum=200;
%最大迭代
x=[0,0,1,1;
0,1,0,1];
t=[1,0,0,0];
x=[x;
1,1,1,1];
sima=0.9;%学习率
w=[0,0,0]; %加上偏置b后为三维输入向量
for i=1:terminalnum
y=w*x;
y=sgn(y);
dy=t-y;
y
%输出
dy
%输出
flag=1;
for m=1:4
if abs(dy(m))>10^-10
flag=0;
end
end
if flag==1
break;
end
w=w+sigma*dy*d;
w
%输出
end
fprintf('迭代次数: %d',i);
我们看一下输出
迭代次数: 1>> //=============================
y =
0 0 0 0
dy =
1 0 0 0
w =
0 0 0.9000
迭代次数: 2>> //=============================
y =
1 1 1 1
dy =
0 -1 -1 -1
w =
-1.8000 -1.8000 -1.8000
迭代次数: 3>> //=============================
y =
0 0 0 0
dy =
1 0 0 0
w =
-1.8000 -1.8000 -0.9000
迭代次数: 4>> //=============================
y =
0 0 0 0
dy =
1 0 0 0
w =
-1.8000 -1.8000 -0.0000
迭代次数: 5>> //=============================
y =
0 0 0 0
dy =
1 0 0 0
w =
-1.8000 -1.8000 0.9000
迭代次数: 6>> //=============================
y =
1 0 0 0
dy =
0 0 0 0
六次以后dy为0 也就是与预期输出相符。
结束语
利用单层感知机,我们可以解决很多线性可分的分类,而且非常方便,但是对线性不可分问题无能为力,下一节我们会讨论线性不可分的问题。