机器学习笔记(五)决策树算法及实践
决策树是机器学习中相当经典的一种算法,既可以用作分类,也可以用作回归,同时还适合做集成学习用于随机森林等等,今天就来好好介绍一下决策树算法。
首先,决策树的思想就是非常容易理解的。通俗地讲就是拿到一堆样本之后,我首先根据某个特征,将样本划分为几类,然后在划分的每一类中,又根据新的特征再划分为若干类,这样重复的进行下去,总会达到一个效果,就是所有的样本都有且有唯一一条规则与之对应,这样决策树的构建就完成了。书面地讲就是从一个根节点出发根据某一特征划分成若干个子节点,再根据某一特征递归地划分下去,直到所有的样本都包含在内。其中中间节点通常表示样本的某一特征或者属性,而最后的叶节点则表示某一个类。
决策树的思想是十分直观的,那么问题来了,怎么去选择划分的特征呢?之前无论是线性回归还是Logistic回归,我们都给出了损失函数,然后根据损失函数去优化,那么决策树的损失函数是什么呢?接下来我们就来回答这两个问题。
常用的决策树算法主要有以下三种:
1 ID3算法
2 C4.5算法
3 CART算法
这三种算法的区别就在于选择特征的标准,具体如下。
ID3算法采用信息增益作为选择特征的依据。为了度量一个随机变量的不确定度,我们给出了熵的定义
那如果随机变量中的某个特征已知,那么在已知该特征的情况下,该随机变量的熵也就是条件熵是
有了条件熵之后,我们就可以计算已知某特征对随机变量熵的下降,我们就把这个下降的熵称之为信息增益,即
在实际的应用当中,由于我们这些所有的概率都只能根据现有数据估计,所以我们把根据样本分布得来的熵称为经验熵及条件经验熵。假设一组数据,总共有D个样本,K个分类,每个分类有Ck个样本,那么经验熵就是
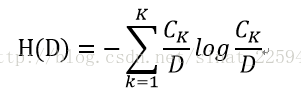
假设根据特征A可以把样本划分为n部分,并且每一部分中属于第K类的样本有Cik个,那么条件经验熵就是

两者相减我们就得到了特征A带来的信息增益,然后根据不同特征的信息增益选择最后的特征对样本进行划分,并且递归的进行下去,就能得到我们最后的决策树。
而C4.5算法与ID3算法仅有一些小小的不同,那就是它所选用的特征是信息增益比而非是信息增益,之所以这么做的主要原因是使用信息增益作为特征选择的标准,容易偏向于那些取值比较多的属性,导致训练出来的树非常的庞大然而深度不深的树,非常容易导致过拟合,在测试集上表现不好。而采用信息增益比则有效地抑制了这个缺点,因为取值多的特征,以它作为根节点的单节点树的熵很大,导致信息增益比减小,在特征选择上会更加合理,信息增益比定义为
树的构建与ID3如出一辙,没什么多讲的。
最后一种CART树,全称是分类和回归树,既可用于分类也可以用于回归。它划分特征所用的标准是Gini系数,定义如下
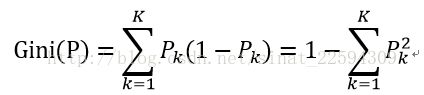
我们都知道熵可以表示随机变量的不确定度,那么为什么Gini系数也可以呢。
简单地考虑一个二分类的情况,假设我们预测这个类是正类的概率为P,如果P小于0.5,那我就预测其为负类,正确概率1-P,如果P大于0.5,则预测为正类,正确概率P,那么醉不确定的情况出现在0.5处,其实分类误差率就是max(P,1-P),而对于Gini系数P(1-P),不仅在0.5处取得最大值,而且关于0.5对称,与分类误差率一模一样,我们在Python中画出二分类的分类误差率、Gini系数和1/2熵。
import numpy as np
from matplotlib import pyplot as plt
p=np.linspace(0.001,1,100,endpoint=False)
gini=2*p*(1-p)
ent=-(p*np.log2(p)+(1-p)*np.log2(1-p))/2
error=1-np.max(np.vstack((p,1-p)),0)
plt.plot(p,gini,'r-',label='Gini')
plt.plot(p,ent,'b-',label='Entropy')
plt.plot(p,error,'g-',label='Error')
plt.legend(loc='upper right')
plt.show()
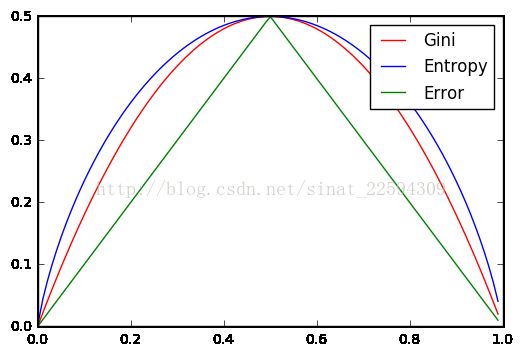
有了Gini系数的概念之后,我们就可以回到上面构建决策树的过程,一步步的特征选择递归构建决策树。
到目前为止我们回答了第一个问题,特征的选择。那么第二个问题,损失函数是什么呢?或者说我们如何来评价决策树的效果呢?
对于构建好的决策树的叶节点,假如分到该节点所有样本都属于同一类,那么分类效果最好,熵最小,如果有多个类别的话,分类效果相对较差,所以用熵衡量是合适的,另外再考虑到不是分到所有的叶节点的数目都是一致的,所以用样本数目做一个加权,得到评价函数

这个值越小表明分类效果越好,与训练数据的符合程度越高。但实际情况中,树的深度太深往往意味着过拟合,导致在训练集上表现很好,但测试集上很差,所以为了提高决策树的泛化能力,加入一个正则项,控制数的复杂度,所以新的评价函数为

第一项表征对训练数据预测的误差,第二项表征树的复杂程度,其中|T|为叶节点的个数。
当然了,有了损失函数我们就可以对树进行优化。思路大概是这样,从完全树T0开始,剪枝去除部分节点得到T1,重复进行,直至仅剩根节点的树Tk,然后用验证集分别对这K个树进行评价,选出最有的那棵树。这里还有个概念称之为剪枝系数,它的计算是通过假设不剪枝和仅保留该节点的评价函数值相同得出的

剪枝的实际过程的操作就是不断寻找最小剪枝系数的节点进行剪枝,直到最后只剩一个根节点,得到k个决策树在验证集上选择最优的。
讲了这么多的决策树理论知识,我们现在在Python中做一个十分简单的应用。就用sklearn自带的鸢尾花数据。
import numpy as np
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn import datasets
#读取数据,划分训练集和测试集
iris=datasets.load_iris()
x=iris.data[:,:2]
y=iris.target
x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.7, random_state=1)
#模型训练
model=DecisionTreeClassifier(max_depth=3)
model=model.fit(x_train,y_train)
y_test_hat=model.predict(x_test)
res=y_test==y_test_hat
acc=np.mean(res)
print '训练集上的正确率是%.2f%%'%(acc*100)
输出为:训练集上的正确率是75.56%
比较一下不同深度对预测准确率的影响
#模型训练
depth_test=np.linspace(1,10,11)
accurate=[]
for depth in depth_test:
model=DecisionTreeClassifier(max_depth=depth)
model=model.fit(x_train,y_train)
y_test_hat=model.predict(x_test)
res=y_test==y_test_hat
acc=np.mean(res)
accurate.append(acc)
print '训练集上的正确率是%.2f%%'%(acc*100)
from matplotlib import pyplot as plt
plt.plot(depth_test,accurate,'r-')
plt.grid()
plt.title('Accuracy by tree_depth')
plt.show()
输出为
训练集上的正确率是55.56%
训练集上的正确率是55.56%
训练集上的正确率是75.56%
训练集上的正确率是75.56%
训练集上的正确率是75.56%
训练集上的正确率是75.56%
训练集上的正确率是64.44%
训练集上的正确率是64.44%
训练集上的正确率是62.22%
训练集上的正确率是60.00%
训练集上的正确率是62.22%

从图中可以看出,并不是随着决策树深度的增加预测的准确率一定会上升,所以实际应用中还是要根据数据选择合适的深度。
当然,DecisionTreeClassifier可以设置的参数还有以下这些:
1 特征选择标准criterion(默认是Gini,还可以选择熵)
2 特征划分点标准splitter(默认是最佳,如果数据量很大也可以改成随机)
3 最大考虑特征max_features(默认是所有,如果特征特别多可以改成log2,sqrt等)
4 节点再划分最小样本数min_samples_split(默认是2,样本量巨大时可适当调高)
当然还有一些其他的参数DecisionTreeClassifier(self, criterion='gini', splitter='best',max_depth=None, min_samples_split=2, min_samples_leaf=1,min_weight_fraction_leaf=0.0, max_features=None, random_state=None,max_leaf_nodes=None, min_impurity_split=1e-07, class_weight=None,presort=False),大家可以根据需要调整。

