计数排序

 

 

原理分析

注意： 计数排序用于整数排序的。

假定20个随机整数的值如下：

9，3，5，4，9，1，2，7，8，1，3，6，5，3，4，0，10，9 ，7，9

建一个11位长度的数组：

如何给这些无序的随机整数排序呢？

非常简单，让我们遍历这个无序的随机数列，每一个整数按照其值对号入座，对应数组下标的元素进行加1操作。

比如第一个整数是9，那么数组下标为9的元素加1：

第二个整数是3，那么数组下标为3的元素加1：

继续遍历数列并修改数组......

最终，数列遍历完毕时，数组的状态如下：

数组每一个下标位置的值，代表了数列中对应整数出现的次数。

有了这个“统计结果”，排序就很简单了。直接遍历数组，输出数组元素的下标值，元素的值是几，就输出几次：

0，1，1，2，3，3，3，4，4，5，5，6，7，7，8，9，9，9，9，10

显然，这个输出的数列已经是有序的了。

这就是计数排序的基本过程，它适用与一定范围内的整数排序。在取值范围不是很大的情况下，它的性能甚至快于那些时间复杂度为O(nlogn)的排序。

最初代码：

public static int[] countSort(int[] array) {
    //1.得到数列的最大值
    int max = array[0];
    for(int i=1; i max){
            max = array[i];
        }
    }
    //2.根据数列最大值确定统计数组的长度
    int[] countArray = new int[max+1];
    //3.遍历数列，填充统计数组
    for(int i=0; i

优化

以上代码存在一些问题，例如如果我们的数列是: 90，95, 94, 93, 97, 93, 98, 99这样，则数列的最爱长度是99，但最小整数是90，如果创建长度为100的数组，那么前面从0到89的空间位置将浪费了。

我们只要不再以输入数列的最大值+1作为统计数组长度，而是以数列最大值-最小值+1作为统计数组的长度即可。

同时，数列的最小值作为一个偏移量，用于计算整数在统计数组的小标。

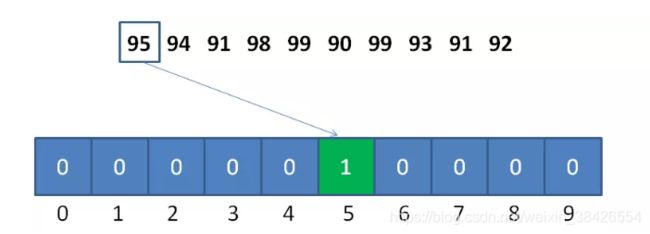
以刚才的数列为例，统计数组的长度为  99-90+1 = 10 ，偏移量等于数列的最小值 90 。

对于第一个整数95，对应的统计数组下标是 95-90 = 5，如图所示：

以上的确堆计数排序进行了优化，但朴素版的计数排序只是简单地按照统计数组的下标输入元素值，并没有真正给原始数列进行排序。

如果只是单纯给整数排序，这样做没有问题，但如果在显示业务里，例如给学生考试分数进行排序，遇到相同的分数就会分不清谁是谁。

例如以下例子：

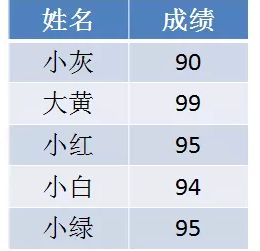
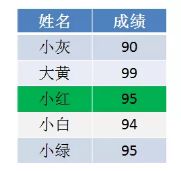
给定一个学生的成绩表，要求按成绩从低到高排序，如果成绩相同，则遵循原表固有顺序。

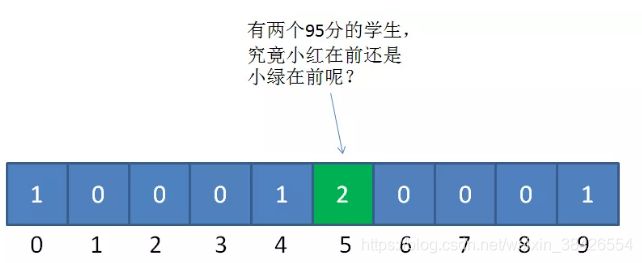
那么，当我们填充统计数组以后，我们只知道有两个成绩并列95分的小伙伴，却不知道哪一个是小红，哪一个是小绿：

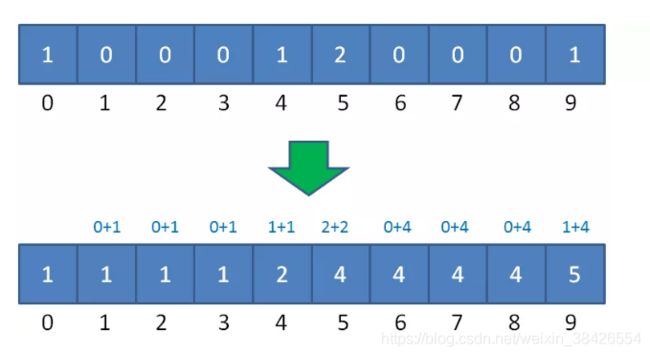
下面的讲解会有一些烧脑，请大家扶稳坐好。我们仍然以刚才的学生成绩表为例，把之前的统计数组变形成下面的样子：

这是如何变形的呢？统计数组从第二个元素开始，每一个元素都加上前面所有元素之和。

为什么要相加呢？初次看到的小伙伴可能会觉得莫名其妙。

这样相加的目的，是让统计数组存储的元素值，等于相应整数的最终排序位置。比如下标是9的元素值为5，代表原始数列的整数9，最终的排序是在第5位。

接下来，我们创建输出数组sortedArray，长度和输入数列一致。然后从后向前遍历输入数列：

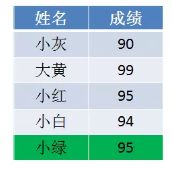
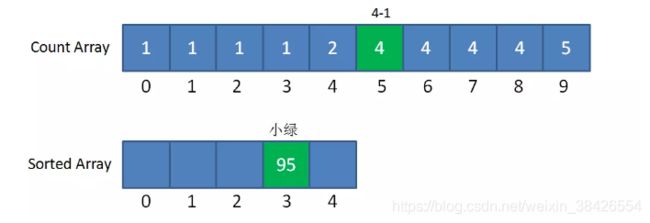
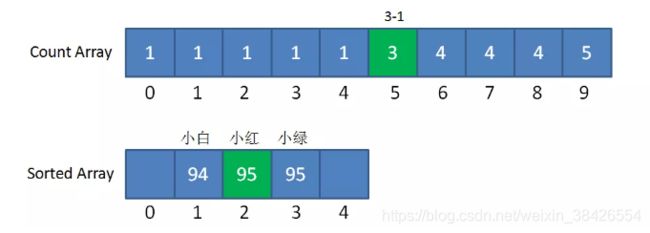
第一步，我们遍历成绩表最后一行的小绿：

小绿是95分，我们找到countArray下标是5的元素，值是4，代表小绿的成绩排名位置在第4位。

同时，我们给countArray下标是5的元素值减1，从4变成3,，代表着下次再遇到95分的成绩时，最终排名是第3。

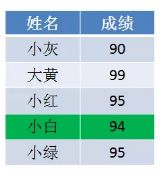
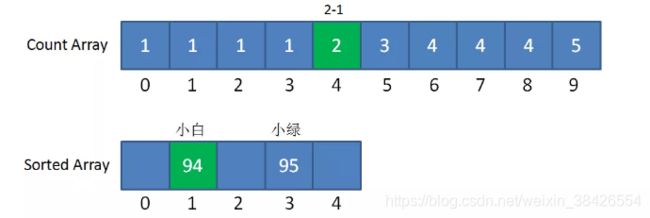
第二步，我们遍历成绩表倒数第二行的小白：

小白是94分，我们找到countArray下标是4的元素，值是2，代表小白的成绩排名位置在第2位。

同时，我们给countArray下标是4的元素值减1，从2变成1,，代表着下次再遇到94分的成绩时（实际上已经遇不到了），最终排名是第1。

第三步，我们遍历成绩表倒数第三行的小红：

小红是95分，我们找到countArray下标是5的元素，值是3（最初是4，减1变成了3），代表小红的成绩排名位置在第3位。

同时，我们给countArray下标是5的元素值减1，从3变成2,，代表着下次再遇到95分的成绩时（实际上已经遇不到了），最终排名是第2。

这样一来，同样是95分的小红和小绿就能够清楚地排出顺序了，也正因此，优化版本的计数排序属于稳定排序。

代码：

public static int[] countSort(int[] array) {
    //1.得到数列的最大值和最小值，并算出差值d
    int max = array[0];
    int min = array[0];
    for(int i=1; i max) {
            max = array[i];
        }
        if(array[i] < min) {
            min = array[i];
        }
    }
    int d = max - min;
    //2.创建统计数组并统计对应元素个数
    int[] countArray = new int[d+1];
    for(int i=0; i=0;i--) {
        sortedArray[countArray[array[i]-min]-1]=array[i];
        countArray[array[i]-min]--;
    }
    return sortedArray;
}
public static void main(String[] args) {
    int[] array = new int[] {95,94,91,98,99,90,99,93,91,92};
    sortedArray = countSort(array);
    System.out.println(Arrays.toString(sortedArray));
}

这里的第四步倒序遍历原始数列，因为countArry数组中的值不再是元素的个数，而是元素的排名，这样的话，遍历出来的sortedArray[countArray[array[i]-min]-1]则是对应的值。即sortArray[排序的位置对应的值] = sortArray[值]。

 

局限性

1.当数列最大最小值差距过大时，并不适用计数排序。

比如给定20个随机整数，范围在0到1亿之间，这时候如果使用计数排序，需要创建长度1亿的数组。不但严重浪费空间，而且时间复杂度也随之升高。

2.当数列元素不是整数，并不适用计数排序。

如果数列中的元素都是小数，比如25.213，或是0.00000001这样子，则无法创建对应的统计数组。这样显然无法进行计数排序。