《机器学习》- 支持向量机SVM
重新学了一遍周志华老师《机器学习》中的支持向量机,这一章数学公式特别多,不容易弄明白,但只要深入学习后,你就会发现了数学是真的很美,推导其中公式后得到的结论实在是太棒了,下面让我们一起见证奇迹吧(讲解顺序和书中一致,但是有些有疑问的或者涉及公式推导的地方,我会详细讲解,小伙伴们最好拿起笔和纸和我一起动手推导)。
SVM引入
给定训练样本集 D=(x1,y1),(x2,y2),...,(xm,ym),yi∈−1,1 ,分类学习最基本的想法就是基于训练集 D 在样本空间中找到一个划分超平面,将不同类别的样本分开。但是能将训练样本分开的划分超平面可能有很多,那么应该选择哪个呢?因此,SVM就此诞生,它的目的是找到最大程度分离训练样本的那个划分超平面,即对未见示例的泛化能力最强。
划分超平面的求解
既然知道了SVM的目的,那么下面就讲解如何求出这个能最大程度分离训练样本的划分超平面。
在样本空间中,划分超平面可通过如下线性方程描述:
wTx+b=0 (1)
其中, w=(w1;w2;...;wd) 为法向量,决定了超平面的方向; b 为位移项,决定了超平面与原点之间的距离,显然,划分超平面可被法向量 w 和位移 b 确定,下面将其记为 (w,b) 。样本空间中任意点 x 到超平面 (w,b) 的距离为
r=∣∣wTx+b∣∣||w|| (2)
假设超平面 (w,b) 能将训练样本正确分类,即对于 (xi,yi)∈D ,若 yi=+1 ,则 wTx+b>0 ;若 yi=−1 则 wTx+b<0 。令
{wTxi+b≥+1,yi=+1wTxi+b≤−1,yi=−1 (3)
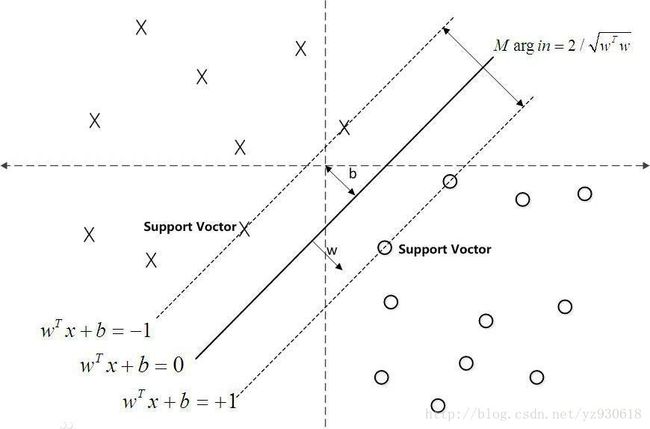
如图,距离超平面最近的这几个训练样本使得式(3)的等号成立,它们被称为“支持向量”(support vector)
两个异类支持向量到超平面的距离之和为
γ=2||w|| (4)
则它被称为“间隔”(margin)
SVM的目的就是要找到具有“最大间隔”的划分超平面,即找到能满足式(3)中约束的参数 w 和 b ,使得 γ 最大:
{max2||w||s.t.yi(wTxi+b)≥1,i=1,2,...,m (5)
显然,上述最优化问题可以转化为:
{min12||w||2s.t.yi(wTxi+b)≥1,i=1,2,...,m (6)
对偶问题
在讲解如何求解(6)中优化问题之前,先叙述下什么是对偶问题:
对于下列优化问题:
⎧⎩⎨⎪⎪minf(x)s.t,hi(x)=0,i=1,2...,mgj(x)≤0,j=1,2...,n (7)
引入拉格朗日乘子 λ=(λ1,λ2,...,λm)T 和 μ=(μ1,μ2,...,μn)T ,将有约束问题转化为无约束问题,相应的拉格朗日函数为:
L(x,λ,μ)=f(x)+∑mi=1λihi(x)+∑nj=1μjgj(x) (8)
那么,可引入求(8)中的最优解的KKT条件为:
⎧⎩⎨⎪⎪⎪⎪gj(x)⩽0μj≥0μjgj(x)=0 (9)
(KKT条件是满足强对偶条件的优化问题的必要条件,可以这样理解:我们要求min f(x), L(a, b, x) = f(x) + a*g(x) + b*h(x),a>=0,我们可以把f(x)写为:max_{a,b} L(a,b,x),为什么呢?因为h(x)=0, g(x)<=0,现在是取L(a,b,x)的最大值,a*g(x)是<=0,所以L(a,b,x)只有在a*g(x) = 0的情况下才能取得最大值,否则,就不满足约束条件,因此max_{a,b} L(a,b,x)在满足约束条件的情况下就是f(x),因此我们的目标函数可以写为 min_x max_{a,b} L(a,b,x),如果用对偶表达式: max_{a,b} min_x L(a,b,x),由于我们的优化是满足强对偶的(强对偶就是说对偶式子的最优值是等于原问题的最优值的),所以在取得最优值x0的条件下,它满足 f(x0) = max_{a,b} min_x L(a,b,x) = min_x max_{a,b} L(a,b,x) =f(x0))
该优化问题可以从两个角度来考察,即“主问题”和对偶问题。对主问题(7),基于式(8),其拉格朗日“对偶函数” τ:Rm×Rn→R 定义为
τ(λ,μ)=infL(x,λ,μ)=inf(f(x)+∑mi=1λihi(x)+∑nj=1μjgj(x)) (10)
拉格朗日对偶函数就是把拉格朗日函数看成x的函数所找到的最小值。若 x~∈D 为主问题(7)可行域中的点,则对任意 μ⩾0 和 λ 都有:
∑mi=1λihi(x)+∑nj=1μjgj(x)⩽0 (11)
进而有
τ(λ,μ)=infL(x,λ,μ)≤L(x~,λ,μ)≤f(x~) (12)
若主问题(7)的最优解为p^{*},则对任意 μ⩾0 和 λ 都有
τ(λ,μ)≤p∗ (13)
即对偶函数给出了主问题最优解的下界,显然,这个下界取决于 μ 和 λ 的值。于是,一个很自然的问题产生了,基于对偶函数能获得的最好的下界是什么?这就引出了优化问题
maxτ(λ,μ)s.t.μ≥0 (14)
式(14)就是主问题(7)的对偶问题。在推导对偶问题时,常通过将拉格朗日乘子 L(x,λ,μ) 对 x 求导并令导数为0,来获得对偶函数的表达形式。
回归求解式(6)中的优化问题,首先,对式(6)使用拉格朗日乘子法:
L(w,b,α)=12∥w∥2+∑mi=1αi(1−yi(wTxi+b)) (15)
其中, α=(α1;α2;...;αm) 。令 L(w,b,α) 对 w 和 b 的偏导为零:
由于 L(w,b,α)=12∥w∥2+∑mi=1αi(1−yi(wTxi+b))=12wTw+∑mi=1αi−∑mi=1αiyiwTxi−∑mi=1αiyib (16)
且向量积对列向量 x 求导运算法则为
d(uTv)dx=d(uT)dxv+d(vT)dxu (17)
所以,
dLdw=d(12wTw)dw∑mi=1d(αiyiwTxi)dw=d(12wT)dww+dwTdw(12wT)T−∑mi=1αiyixi=w−∑mi=1αiyixi
dLdb=−∑mi=1αiyi (18)
令 dLdw=0,dLdb=0 ,则
{w=∑mi=1αiyixi0=∑mi=1αiyi (19)
将(19)带到(15)中,就得到式(15)的拉格朗日对偶函数为
τ(α)=∑mi=1αi−12∑mi=1∑mj=1αiαjyiyjxTixj (20)
则,主问题(6)的对偶问题为:
⎧⎩⎨⎪⎪⎪⎪maxτ(α)=max∑mi=1αi−12∑mi=1∑mj=1αiαjyiyjxTixjs.t.∑mi=1αiyi=0,αi≥0,i=1,2,...,m (21)
在解出 α 后,求出 w 和 b 即可得到模型:
f(x)=wTx+b=∑mi=1αiyixTix+b (22)
从对偶问题(21)中解出的 αi 是式(15)中的拉格朗日乘子,它正好对应着训练样本 (xi,yi) ,而求解(15)中最优化问题需要满足KKT条件:
⎧⎩⎨⎪⎪αi≥0yif(xi)−1≥0αi(yif(xi)−1)=0 (23)
(KKT条件解释:如果 αi<0 ,而由于 yif(xi)≥1 ,所以式(15)无最大值 ;如果 yif(xi)−1<0 ,如果令 αi=−∞ ,那么也无最大值;由于 αi(1−yif(xi))⩽0 ,所以当 αi(yif(xi)−1)=0 的时候,才可以取得最大值)。
则,对于任意训练样本 (xi,yi) ,总有 αi=0 或者 yif(xi)=1 。若 αi=0 ,则该样本将不会在式(22)中的求和中出现,也就不会对 f(x) 有任何影响;若 αi>0 ,则必有 yif(xi)=1 ,此时所对应的样本点位于最大间隔边界上,是一个支持向量。这就说明了SVM的一个激动人心的重要性质:
只有支持向量才会影响最终模型,其他训练样本都不需要保留!
SMO求解对偶问题
虽然到此,我们已经得到了SVM重要的结论,但是还有一个问题没有解决,就是如何求解(21)中的对偶问题。SMO就是一个非常著名求解这类问题的高效算法,下面开始讲解如何利用SMO进行求解:
SMO的基本思路是先固定 αi 之外的所有参数,然后求 αi 上的极值。由于存在约束 ∑mi=1αiyi=0 ,若先固定 αi 之外的其他变量,则 αi 可由其他变量导出。于是,SMO每次选择两个变量 αi 和 αj ,并固定其他参数,这样,在参数初始化后,SMO不断执行如下两个步骤直至收敛。
- 选取一对需要更新的变量 αi 和 αj ;
- 固定 αi 和 αj 之外的的参数,求解式(21)获得更新后的 αi 和 αj 。
注意到,只要所选取的 αi 和 αj 中有一个不满足KKT条件(23),目标函数就会在迭代后增大,因为假设 αi 不满足KKT条件,这说明 αi<0 ,所以 αi(yif(xi)−1)>0 则在迭代后目标函数就会在迭代后增大。因此SMO采用下面方式选择变量:使选取的两个变量所对应样本之间的间隔最大。
SMO算法之所以高效,恰由于在固定其他参数后,仅优化两个参数的过程能做到非常高效。具体来说,仅考虑 αi 和 αj 时,式(21)中的约束可重写为
αiyi+αjyj=c,αi≥0,αj≥0 (24)
其中, c=−∑mk≠i,jαkyk
用式(24)消去(21)中的变量 αj ,则得到一个关于 αi 的单变量二次规划(目标函数是二次函数)问题,仅有的约束是 αi≥0 。这样的二次规划问题具有闭式解,于是不用调用数值优化算法即可高效地计算出更新后的 αi 和 αj 。这样再迭代直至收敛后,就可以计算 w 的值了。
那么,如何确定偏移项 b 的值呢?由于对任意支持向量 (xs,ys) 都有 ysf(xs)=1 ,即
ys(∑i∈SαiyixTixs+b)=1 (25)
其中 S 为所有支持向量的下标集。理论上,可以选出任意支持向量并通过求解式(25)获得 b ,但有一个更鲁棒的做法,使用所有支持向量求解的平均值:
b=1|S|∑s∈S(1/ys−∑i∈SαiyixTixs) (26)
到此,利用SVM求解线性可分的问题就讲解完了。但现实生活中,训练样本也许并不是线性可分的,那么我们可以将样本从原始空间映射到一个更高维的特征空间中,使得样本在这个特征空间内线性可分。接下来的思路跟上述求解线性问题一样了。
前面我们一直假定训练样本在样本空间中是能被完全分开的,但是,现实生活中,往往很难做到这点,所以解决该问题的一个办法就是允许支持向量机在一些样本上犯错,从而引入了“软间隔”的概念,即,允许某些样本不满足约束条件 yi(wTxi+b)⩾1 。
这两类现实中的情况,在这里就不细说了,就按照线性可分的思路,都可以弄明白。
另外,由于SVM一般用于解决分类问题,那么对于回归问题,我们引入了SVR,即支持向量回归算法。给定训练样本 D=(x1,y1),(x2,y2),...,(xm,ym),yi∈R ,我们希望学得一个形如 f(x)=wTx+b 的回归模型。传统的回归问题是基于模型输出 f(x) 和真实输出 y 之间的差别来计算损失,当且仅当 f(x) 和 y 完成相同时,损失才为零。而SVR假设能容忍 f(x) 和 y 之间有一定的偏差 ε ,仅当大于这个偏差时,才计算损失。
如图所示,这相当于以 f(x) 为中心,构建了一个宽度为 2ε 的间隔带,若训练样本落入此间隔带,则认为是被预测正确的。
所以,我们要做的是使得损失尽可能小,则SVR问题可形式化为
min12∥w∥2+C∑mi=1ιε(f(xi)−yi) (27)
其中, ιε={0,if|z|⩽ε|z|−ε,otherwise 是损失函数。
则该问题的求解思路依然和线性可分的求解思路一致了。
好了,到此,SVM的所有内容基本上已经讲解完了。