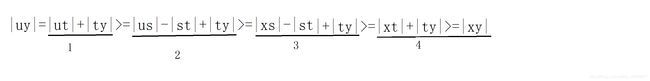广度优先搜索的用处
用处一:
判断图中是否有环 找出图的树边
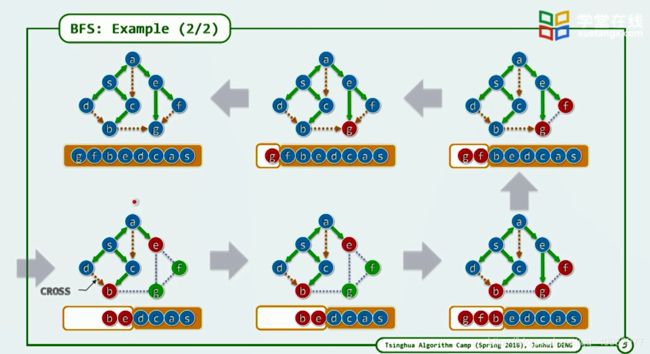
首先我们给出广度优先搜索的具体执行过程,以下面两个图为例:
接上图:
首先对这两个图做一点说明:
一:图中绿色的点代表未访问过的顶点
二:图中红色的点代表正在访问的点(正在队列中的点)
三:图中蓝色的点代表已经访问完成的点(已经出队的点)
四:图中绿色箭头所表示的边代表进行广搜操作后真正走过的边
五:图中红色虚线箭头所表示的边代表广搜操作无法走的边
六:图中灰色虚线所表示的边代表还未访问的边
如何判断图中是否有环:
如果对图进行完广度优先搜索后,存在上述红色虚线箭头所表示的边,那么说明图中有环。
找出图中的树边:
对图进行完广度优先搜索后,图中所有的绿色箭头所表示的边就是树边。
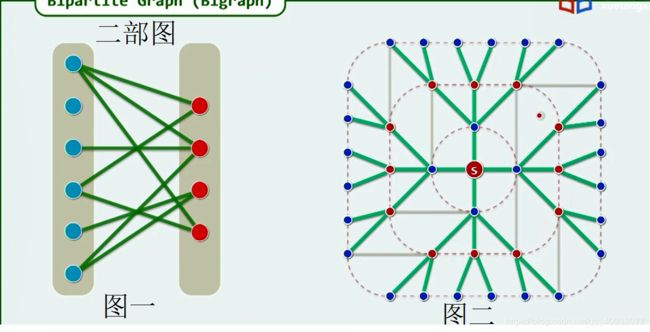
判断图是否为二部图:.
如果给定图的所有边都是图二中绿色或者灰色的边,不存在虚线所示的边,那么我们就可以确定这个图为二部图。
思考:下图中是否会存在从A到D的那种黑色边?
答:不会,因为如果存在从A到D的黑色边,那么D点到S点的最短距离为2(这里我们假设所有的边的权值都为1),而不是3,那么我们在进行BFS时就不可能选择B->C->D这条线路了,而是选择A->D这条线路,因为A->D这条线路的距离短,这就产生矛盾了。
下面我们来思考一个例题:
例题一:
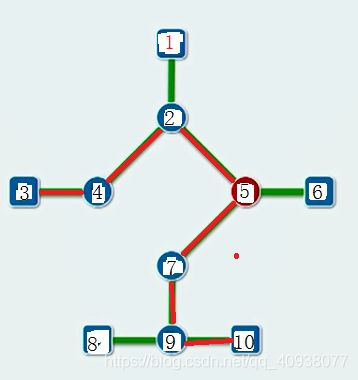
给定一棵多叉树,每条边的权值都为1,让你找出树中距离最长的两个顶点之间的距离。
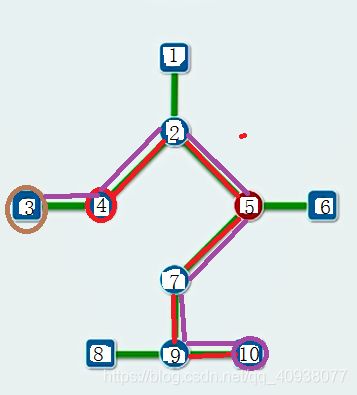
例如在上图所示的树中’,距离最长的两个顶点为3号顶点和10号顶点(或者8号顶点),最长距离为6(图中红色边所示)。
解析:
1:如果给定的树是一个二叉树,我们可以运用分治的思想进行递归求解。对于当前顶点,一共有三种距离最长的情况:
情况一:最长的距离在当前顶点的左子树中
情况二:最长的距离在当前顶点的右子树中
情况三:最长的距离跨越当前顶点(左子树和右子树中都占一点)
2:如果给定的树不是一个二叉树(其实也可以用上面的方法求解,但是我不会,~~~~(>_<)~~~~),先从树中任意选取一个点进行一次BFS,得到离该顶点距离最远的顶点(就是BFS算法中最后一个出队的顶点),然后再对得到的顶点进行一次BFS,又会得到一个距离这次顶点最远的顶点,而这两个顶点之间的距离就是我们要求的结果。
首先,我们选择4号顶点进行一次BFS,得到距离4号顶点最远的10号顶点,然后再对10号顶点进行一次BFS,得到距离10号顶点最远的3号顶点,3号顶点和10号顶点之间的距离就是我们要求的距离。
代码应该好写,这里就不给出了。
证明这种解法的正确性:
再证明正确性之前,我们必须先知道一些术语。
图的直径:在一个图中,距离最远的两个顶点之间的连线称作图的直径。
直径端点:图中距离最远的两个顶点。
在上面的解法中,我们第一次进行BFS后所得到的那个顶点就是一个直径端点(步骤一),然后以这个直径端点为源点,再进行一个BFS,就可以得到另一个直径端点(步骤二),最长距离也就求出来了。
步骤二很好理解,不需要证明。关键在于证明步骤一(为啥进行完第一个BFS后,得到的那个顶点就是一定是一个直径端点)。
证明过程如下(只列举了一般情况,实际有很多情况,我自己还没搞清楚,~~~~(>_<)~~~~):
假设第一次选定s点为源点,进行完BFS后,所得到的顶点u不是直径顶点,而直径顶点为x,y。
我们只需要证明从u到y(或者从u到x)的距离>=从x到y的距离:
(如果是大于的话,说明u到y之间的连线是直径,而x到y之间的连线不是直径,这时u是直径顶点)
(如果是等于的话,说明u到y之间的连线是其中一条直径,x到y之间的连线是另一条直径,这时u也是直径顶点)
上面是证明公式,我们来仔细讲讲具体的转化过程:
1式转化为2式:通过上图的右图可以得到|ut|=|us|-|st|(这只是一种情况,还有一种情况就是s点在u点到t点这条线路上,此时|ut|>|us|-|st|)。
2式转化为3式:|us|>=|xs|,因为我们假定了u点是s点进行完BFS后所得到的点,所以u点到s点的距离肯定是最大的(BFS算法的性质),所以|xs|<=|us|。
3式转化为4式:|xs|-|st|=|xt|,通过上图的右图可以得到(当然还有其他情况,所以是大于等于)。
最后|xt|+|ty|=|xy|很好想。
通过一系列连等,我们最终可以得到|uy|>=|xy|,即u到y的距离>=x到y的距离。证毕。