2020第十一届7月蓝桥杯大赛软件类B组C/C++省赛题解
2020第十一届7月蓝桥杯大赛软件类B组C/C++省赛目录
-
-
- 试题 A：跑步训练（结果填空）
- 试题 B：纪念日（结果填空）
- 试题 C：合并检测（结果填空）
- 试题 D：REPEAT 程序（结果填空）
- 试题 E：矩阵（结果填空）
- 试题 F：整除序列（程序设计）
- 试题 G：解码（程序设计）
- 试题 H：走方格（程序设计）
- 试题 I：整数拼接（程序设计）
- 试题 J：网络分析（程序设计）
-
试题 A：跑步训练（结果填空）
题意：
代码：
#include答案： 3880（注意答案是以秒为单位输出！）
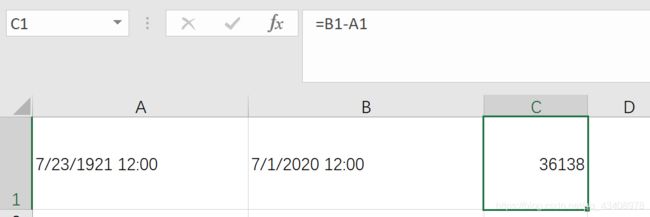
试题 B：纪念日（结果填空）
题意：
做法：
答案：52038720（36138 * 24 * 60）
试题 C：合并检测（结果填空）
题意：
做法：概率杀我 ，设A国共有100人，那么合并检测需要用的试剂为 100 k \frac{100}{k} k100个，均匀分布可以认为100个人里面就有一个人感染，所以，对于这一个人还需要个试剂，结果就是 100 k + k \frac{100}{k}+k k100+k，根据基本不等式，当 100 k = k \frac{100}{k}=k k100=k时，等式取到最小值，这时k=10。
答案：10
试题 D：REPEAT 程序（结果填空）
题意：
做法：用一个栈维护循环次数，模拟即可。
代码：
#include答案：241830
试题 E：矩阵（结果填空）
题意：
做法：一看这题像dp，但是想不出转移方程 。f[i][j]表示第一行选i个数，第二行选j个数的总方案数，第二行能选的前提是第一行第j列有数。每个状态由上一个行和上一列转化而来，可以选择放在第一行或者第二行。这篇题解简单易懂。
代码：
#include答案：1340
——以下题目通过了 AcWing 的数据测试——
试题 F：整除序列（程序设计）
题意：
做法：记得开long long!!
代码：
#include试题 G：解码（程序设计）
题意：
做法：内部可能有数字有两位以上的情况，坑还是挺多的。
代码：
#include试题 H：走方格（程序设计）
题意：
做法：类似一个经典的dp，方格取数，只要行数和列数都为偶数时不更新dp[i][j]就能做到。
代码：
#include试题 I：整数拼接（程序设计）
题意：
做法：正解就是把所有数扩大几倍后存起来，再用map找，要理解到，对于这些存起来的数字取膜k以后，只有两个数字加起来%k等于0才算一对，后面就能暴力了。用数组存每个数扩大10倍、100倍…十的十次方倍，存入a数组，再用一个vis充当map的作用，顺势记录这个数有多少位。
代码：
#include试题 J：网络分析（程序设计）
题意：
做法：用w数组记录该点所有子孙都需要+的权值，每次合并都下传标记，复杂度n^2，极限卡常
代码：
#include