利用线段树解决RMQ问题
线段树 – 支持动态查询区间最值问题
一.时间复杂度与适用场景
线段树是用O(n)的时间建树,然后每一次查询都是O(logn)的时间复杂度,所以他更适合n大m小的RMQ问题(数值多,但是查询次数少)
同时线段树支持修改节点上的值,是允许动态查询的一种方法。
二.线段树的具体实现过程
1.建树 – build
线段树的建树操作实际上就是叶子节点 = 初始的值,然后从下到上分别取左右儿子中最小的那个的值来更新树节点的值就好了。
黄色代表树的节点,黑色是该节点的值,蓝色的长度代表覆盖区间,例如tree[4] = 4,tree[2] = 2,tree[1]覆盖的区间就是整个区间,tree[2]覆盖的区间就是前两个数;
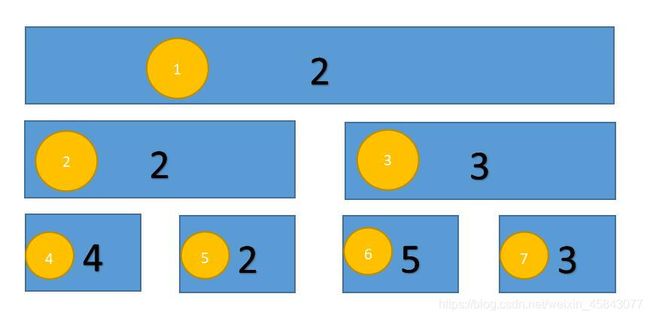
- 建树的时候我们先从①号节点出发,然后输入区间左端点 l 与右端点 r (分别为1,n);
- 向下递归,当 l != r 的时候说明该节点还有左右儿子,分别递归求左儿子(2 * p)与右儿子(2 * p + 1),在递归过程中区间也逐渐二分减小;
- 当 l == r 的时候说明已经到了叶子节点,就更新 tree[ p ] = a[ l ] ,然后向上回溯,更新它父亲节点的值,直到回溯到根节点,也就是建树完成。
代码:
void push_up(int p)
{
int ls = 2 * p;
int rs = 2 * p + 1;
tree[p] = min(tree[ls],tree[rs]);
}
void build(int p, int l, int r)
{
if(l == r) {
tree[p] = a[l];
return ;
}
int ls = 2 * p;
int rs = 2 * p + 1;
int mid = (l+r)/2;
build(ls,l,mid);
build(rs,mid+1,r);
push_up(p);
}
2.更新 – update
线段树的更新和建树很像,都是先一直向下递归+逐渐二分减少区间,直到找到要更新的叶子节点,就更新其值,然后在向上回溯的过程中更新每个覆盖它的区间的最值。
因为是单点修改,所以当不是叶子节点,即 l != r 的时候,就判别一下需要修改的点在当前节点的左儿子上还是右儿子上,然后在递归到该子区间上。
例如:修改 a[ 1 ] = 3,我们就一直在树上递归到 1 -> 2 -> 4(这里是黄色的节点,也就是树的节点),tree[ 4 ] = 3,然后每次在根据其值修改tree[ 2 ]、tree[ 1 ]的值。
代码:
void update(int p,int l,int r,int k,int val)
{
if(l == r)
{
a[k] = val;
tree[p] = val;
return ;
}
int mid = (l + r) / 2;
int ls = 2 * p;
int rs = 2 * p + 1;
if(k <= mid)
update(ls,l,mid,k,val);
else
update(rs,mid+1,r,k,val);
tree[p] = min(tree[ls],tree[rs]);
}
3.查询 – query
查询就只会出现三种情况:
- 所查询的区间与当前节点对应的区间完全没有交集,就返回一个不会影响结果的值。例如求最小值,就返回一个最大值INF,就不会影响结果。
- 所查询的区间完全包含了当前节点对应的区间,就直接返回当前节点的值。
- 如果不满足上述两个条件,就对两个儿子做递归处理,返回两个结果中我们所求的最值,求最大值就返回最大值,求最小值就返回最小值。
代码:
int query(int q_x,int q_y,int l,int r,int p)
{
int res = INF;
if(q_x <= l&&r<=q_y)
return tree[p];
int ls = 2*p;
int rs = 2*p+1;
int mid = (l+r)/2;
if(q_x <= mid)
res = min(res,query(q_x,q_y,l,mid,ls));
if(q_y > mid)
res = min(res,query(q_x,q_y,mid+1,r,rs));
return res;
}
三.模板
#include 四.模板题
hihocoder – 1077 RMQ问题再临-线段树
d == 1的时候更新值,d == 0的时候查询区间最小值
#include