HDU-3081 Marriage Match II（匈牙利算法最大匹配+并查集 && 最大流+二分+并查集）

题目连接

题意： 
     n 个男生 n个女生 玩游戏
     然后 每个女生都可以和她不讨厌的男生结婚，此外她的朋友如果不讨厌某个男生
     这个女生也可以和这个男生结婚
     最后 如果B是A的朋友 C 是B的朋友则 A和C也是朋友
     每次游戏女生会找一个她不讨厌的男生结婚，如果所有女生匹配成功 则进行下一轮游戏
     每个女生只能选择同一个男生一次，问游戏最多能进行几轮

思路：
    1，并查集 
    如果B是A的朋友 C 是B的朋友则 A和C也是朋友 （并查集）
    让女生给所有能连线的男生连线
    2.
    然后女生和男生匹配 可以
        1 KM算法每次匹配完统计匹配数并且把匹配的边都给删掉，并记录次数 
            继续匹配 直到找到最大匹配不等于女生人数（n） ，输出次数 
        2 最大流算法（二分图跑最大流）
            1）建立超级源点超级汇点，从源点出发，到汇点，（源点和女生相连）汇点和男生连线，男女（符合题意）连线
                然后边权全为1, 然后跑最大流，跑一次，然后把这次最大流中用到的男女边删掉，一直跑最大流 直到 最大流小于 n 
                这种时候的弊端 如果每个女孩给每个男孩都有连线  你就需要跑到上限，然后小小优化 
            2） 因为你跑的次数是 0 到 100 我们利用二分假设你跑多少次，直接2分找游戏进行的次数
                这时我们的男女之间的边权还为 1  但是  我们建立的超级源点到女生直接的边权，和男生到超级汇点的边权就变了
                变为我们二分假设的答案 比如说 第一次是 mid = 50 ， 如果源点到汇点的最大流为mid*n 说明游戏可以玩mid轮，然后
                mid继续变大  更新mid直至二分结束，（二分的返回值也是个关键）       

思路已有：
      做题步骤
      1 ：建图 并用并查集 将是朋友的女生 和她们的男生连线
      2 ：建立超级源点汇点，让源点连女生， 汇点连男生， 边权为 Mid （二分） 值
      3 ： 跑最大流 当 mid * n  = 最大流值 时 left = mid + 1 
      4 : 当 mid * n > 最大流时 right = mid - 1; 
      5 : 退出时输出 left - 1   

匈牙利算法AC 代码  ： 时间复杂度 O（V * E）

/*
	二分图匹配匈牙利算法  时间复杂度 O(V * E) 
*/
#include
#include
#include
#include
#include
#include

using namespace std;
const int maxn = 205;
const int INF = 0x3f3f3f3f;
int N, M, F;
int Friend[maxn];
int G[maxn][maxn];
bool Used[maxn];
int Match[maxn]; 
int findFather (int v) {
	if(v == Friend[v]) return v;
	else {
		int F = findFather(Friend[v]);
		Friend[v] = F;
		return F;
	}
}
void Union(int a, int b) {
	int fA = findFather(a);
	int fB = findFather(b);
	if(fA != fB) {
		Friend[fA] = fB;
	}
}
bool Find(int x){
	for(int i = 1; i <= N; ++i) {
		if (G[x][i] && Used[i] == 0) {
			Used[i] = 1;
			if (Match[i] == -1 || Find(Match[i])) {
				Match[i] = x;
				return true;	
			}
		}
	}
	return false;
}
int Solve() {
	int Num = 0;
	for (int i = 1; i <= N; ++i) {
		memset(Used, 0, sizeof(Used));
		if(Find(i)) {
			++Num;
		}
	}

	if (Num == N) {
		for(int i = 1; i <= N; ++i){
			if(Match[i] != -1) {
				G[Match[i]][i] = 0;
			}
		}
		return true;
	} else {
		return false;
	}
}
int main() {
	std::ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0); 
	//freopen("in.txt", "r", stdin);
	//freopen("out.txt", "w", stdout);
	int T;
	cin >> T;
	int a, b, c, Ans;
	while (T--) {
		Ans = 0;
		memset(G, 0, sizeof(G));
		cin >> N >> M >> F;
		for (int i = 1; i <= M; ++i) {
			cin >> a >> b;			
			G[a][b] = 1;
		}
		for (int i = 0; i <= N; ++i) {
			Friend[i] = i;				
		}
		for (int i = 1; i <= F; ++i) {
			cin >> a >> c;
			Union(a, c);
		}
		for (int i = 1; i <= N; ++i) {
			for (int j = 1; j <= N; ++j) {
				if (findFather(Friend[i]) == findFather(Friend[j])) {
					for (int k = 1; k <= N; ++k) {
						if (G[j][k] == 1) {
							G[i][k] = 1;	
						} 
					}
				}
			}
		}
		while (1) {
			memset(Match, -1, sizeof(Match));
			if (Solve()) {
				++Ans;
			} else {
				break;
			}
		}
		cout << Ans << endl;
	}
	
	return 0;
}

最大流AC代码： 时间复杂度 O（二分长度 + O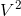（ * E））:

#include
#include
#include
#include
#include
#include 
using namespace std;
const int maxn = 200;
const int maxm = 5e4;
const int inf = 0x3f3f3f3f;
int s, e;
int Cnt;
int N, M, F;
int G[maxn][maxn];
int head[maxn], dis[maxn], curedge[maxn], Friend[maxn];
struct ac {
	int v, c, nex;
}edge[maxm];

void init () {
	Cnt = 0;
	memset(head, -1, sizeof(head));
}

void addedge (int u, int v, int c) {
	edge[Cnt] = {v, c, head[u]};
	head[u] = Cnt++;
	edge[Cnt] = {u, 0, head[v]};
	head[v] = Cnt++;
}
bool Bfs(){
	memset(dis, 0, sizeof (dis));
	queue que;
	que.push(s);
	dis[s] = 1;
	while (!que.empty()) {
		int u = que.front();
		que.pop();
		for (int i = head[u]; i != -1; i = edge[i].nex) {
			int v = edge[i].v;
			int c = edge[i].c;
			if (dis[v] || c == 0) continue;
			dis[v] = dis[u] + 1;
			que.push(v);
		}
	}
	return dis[e] > 0;
}
int Dfs(int u, int flow) {
	if(u == e || flow == 0) return flow;
	for(int i = curedge[u]; i != -1; i = edge[i].nex) {
		int v = edge[i].v;
		int c = edge[i].c;
		if (dis[v] != dis[u] + 1 || c == 0) continue;
		int d = Dfs (v, min(flow, c));
		if (d > 0) {
			edge[i].c -= d;
			edge[i ^ 1].c += d;
			curedge[u] = i;
			return d;	
		} 
	}
	dis[u] = -1;
	return 0;
}
int Dinic() {
	int Sum = 0, d;
	while (Bfs()) {
		for(int i = 0; i <= N * 2 + 1; ++i) 
			curedge[i] = head[i];
		while ( (d = Dfs(s, inf)) > 0) {
			Sum += d;
		}
	}
	return Sum;
}
int findFather (int v) {
	if(v == Friend[v]) return v;
	else {
		int F = findFather(Friend[v]);
		Friend[v] = F;
		return F;
	}
}
void Union(int a, int b) {
	int fA = findFather(a);
	int fB = findFather(b);
	if(fA != fB) {
		Friend[fA] = fB;
	}
}
int Solve (int flow) {
	init();
	for (int i = 1; i <= N; ++i) {
		addedge(s, i, flow);
		addedge(i + N, e, flow);
	}
	for (int i = 1; i <= N; ++i) {
		for (int j = 1; j <= N; ++j) {
			if (G[i][j]) {
				addedge(i, j + N, 1);
			}
		}
	}
	int Temp = Dinic();
	//cout << flow << " " << Temp << endl;
	return Temp;
}
int main () {
	std::ios::sync_with_stdio(false);
	cin.tie(0), cout.tie(0);
	//freopen("in.txt", "r", stdin);
	//freopen("out.txt", "w", stdout);
	int T;
	cin >> T;
	int a, b, c, Ans;
	while (T--) {
		memset(G, 0, sizeof(G));
		Ans = 0;
		cin >> N >> M >> F;
		s = 0;
		e = 2 * N + 1;
		for (int i = 1; i <= M; ++i) {
			cin >> a >> b;
			G[a][b] = 1; 
		}
		for (int i = 0; i <= N; ++i) {
			Friend[i] = i;				
		}
		for (int i = 1; i <= F; ++i) {
			cin >> a >> c;
			Union(a, c); 
		}
		for (int i = 1; i <= N; ++i) {
			for (int j = 1; j <= N; ++j) {
				if (findFather(i) == findFather(j)) {
					for (int k = 1; k <= N; ++k) {
						if( G[j][k] == 1 ) {
							G[i][k] = 1;
						}
					}	
				}
			}
		}
		int left = 0, right = 101;
		int mid;
		int Ans = 0;
		while (left <= right) {
			mid = (left + right)/2;
			int Temp = Solve(mid);
			if (Temp == N * mid) {
				left = mid + 1;
				Ans = mid;
			} else {
				right = mid - 1;
			}
		}
		cout << Ans << endl;
	}
	return 0;
}