AtCoder Grand Contest 002 做题记录

A - Range Product

题意：给定两个整数 a a 、 b b （ a≤b a ≤ b ），判断 ∏bi=ai ∏ i = a b i 的正负形。
−109≤a≤b≤109 − 10 9 ≤ a ≤ b ≤ 10 9
解答：分类讨论即可。

#include 
using namespace std;
typedef long long LL;
inline int rd() {int r;scanf("%d",&r);return r;}
int main() {
    int a = rd(), b = rd();
    if (1LL * a * b <= 0) {
        puts("Zero");
        return 0;
    }
    if (a>0) {
        puts("Positive");
        return 0;
    }
    a = abs(a);
    if (b < 0) a -= abs(b+1);
    puts(a&1 ? "Negative" : "Positive");
    return 0;
}

B - Box and Ball

题意：一开始有 N N 个盒子，每个盒子里面有一个球。第一个盒子里的球是红球，其余的球为白球。接下来有 M M 个操作，每次从 xi x i 盒子中任意取一个球放入 yi y i 盒子中。询问所有操作结束后有多少个盒子内有可能有红球。
2≤N≤105 2 ≤ N ≤ 10 5
1≤M≤105 1 ≤ M ≤ 10 5
1≤xi,yi≤N 1 ≤ x i , y i ≤ N
解答：若一次操作可以将一个盒子的球清空，那么这个盒子就一定没有红球，否则只要有红球可能进入该盒子，那么到最后该盒子就有可能有红球。

#include 
#define N 1000500
#define x first
#define y second
using namespace std;
typedef pair<int,int> pii;
pii t[N];
inline int rd() {int r;scanf("%d",&r);return r;}
int n,m;
int main() {
    n = rd(), m = rd();
    t[1] = pii(1,1);
    for (int i=2;i<=n;i++) t[i] = pii(0, 1);
    for (int i=1;i<=m;i++) {
        int a = rd(), b = rd();
        t[b].x |= t[a].x;
        t[b].y ++;
        t[a].y --;
        if (!t[a].y) t[a].x = 0;
    }

    int ans = 0;
    for (int i=1;i<=n;i++) if (t[i].x) ans++;
    cout << ans << endl;
    return 0;
}

C - Knot Puzzle

题意：给定 N N 条绳子，第 i i 条长度为 ai a i ，现在用 N−1 N − 1 个结将所有绳子连成一条。你可以每次选取长度大于等于 L L 的绳子，将其中一个结解开。询问是否可以将所有结都解开，若可以输出”Possible”并给出方案，否则输出”Impossible”。
2≤N≤105 2 ≤ N ≤ 10 5
1≤L≤109 1 ≤ L ≤ 10 9
1≤ai≤109 1 ≤ a i ≤ 10 9
解答：如果不存在连续的两段绳子 ai a i 和 ai+1 a i + 1 满足 ai+ai+1≥L a i + a i + 1 ≥ L ，则无解。（考虑解开最后一个结时候的情况）。否则以这两段绳子为中心，解开两边的结，最后再解开这个结。

#include 
#define N 1000500
using namespace std;
int n,L,a[N];
inline int rd() {int r;scanf("%d",&r);return r;}
int main() {
    n = rd(), L = rd();
    for (int i=1;i<=n;i++) a[i] = rd();

    int d = 0;
    for (int i=1;iif (a[i]+a[i+1] >= L) d = i;
    if (!d) {
        puts("Impossible");
    } else {
        puts("Possible");
        for (int i=1;iprintf("%d\n",i);
        for (int i=n-1;i>d;i--) printf("%d\n",i);
        printf("%d\n",d);
    }

    return 0;
}

D - Stamp Rally

题意：给定一张 N N 个点 M M 条边的无向图，现在有 Q Q 次游戏，每次游戏两兄弟从 xi x i 和 yi y i 出发，两个人一共要访问过 zi z i 个点（一个人重复访问一个点，或者两个人都访问过的一个点，算作一个点）。 两个人所需要花费的代价为他们所经过的编号最大那条边的编号，要求最小化代价并输出这个代价。
3≤N≤105 3 ≤ N ≤ 10 5
N−1≤M≤105 N − 1 ≤ M ≤ 10 5
1≤Q≤105 1 ≤ Q ≤ 10 5
解答：若询问只有一个，将边从小到大加入无向图，讨论一下判断连通块大小即可。多组询问用整体二分即可。

#include 
#define N 100050
using namespace std;

struct HbFS{int _,x,y,t;}Q[N],tmp[N];
int fa[20][N],siz[20][N],ans[N],T[20];
int a[N],b[N],n,m,q;

inline int rd() {int r;scanf("%d",&r);return r;}

int gf(int dep,int x) {
    return fa[dep][x] == x ? x : fa[dep][x] = gf(dep, fa[dep][x]);
}

void mer(int dep, int x, int y) {
    int p1 = gf(dep, x);
    int p2 = gf(dep, y);
    if (p1 == p2) return ;
    fa[dep][p1] = p2;
    siz[dep][p2] += siz[dep][p1];
    siz[dep][p1] = 0;
}

void solve(int ql,int qr,int vl,int vr,int dep) {
    if (vl == vr) {
        for (int i=ql;i<=qr;i++) ans[ Q[i]._ ] = vl;
        return ;
    }

    int mid = (vl + vr) >> 1;

    while (T[dep]+1 <= mid) {
        T[dep]++;
        int cur = T[dep];
        mer(dep, a[cur], b[cur]);
    }

    int dl = ql, dr = qr;
    for (int i=ql;i<=qr;i++) {
        int p1 = gf(dep, Q[i].x);
        int p2 = gf(dep, Q[i].y);
        if (p1 == p2) {
            if (siz[dep][p1] >= Q[i].t) 
                tmp[dl++] = Q[i];
            else
                tmp[dr--] = Q[i];
        } else {
            if (siz[dep][p1]+siz[dep][p2] >= Q[i].t)
                tmp[dl++] = Q[i];
            else
                tmp[dr--] = Q[i];
        }
    }

    for (int i=ql;i<=qr;i++) Q[i] = tmp[i];
    solve(ql,dl-1,vl,mid,dep+1);
    solve(dr+1,qr,mid+1,vr,dep+1);
}

int main() {
    n = rd(), m = rd();
    for (int i=1;i<=m;i++) a[i] = rd(), b[i] = rd();

    for (int i=1;i<=19;i++)
        for (int j=1;j<=n;j++)
            fa[i][j] = j, siz[i][j] = 1;

    q = rd();
    for (int i=1;i<=q;i++) {
        int x = rd(), y = rd(), t = rd();
        Q[i] = (HbFS){i, x, y, t};
    }
    solve(1,q,1,m,1);
    for (int i=1;i<=q;i++) printf("%d\n",ans[i]);
    return 0;
}

E - Candy Piles

题意： 有 N N 堆糖果，第 i i 堆糖果有 ai a i 个糖果。两个人进行游戏，每一轮可以进行如下操作之一：
1、每堆糖果拿一个。
2、取走最多那一堆糖果。
吃掉最后一个糖果的人判负，求先手胜负。
解答：
从大到小排序，前两种操作可以这么表示。

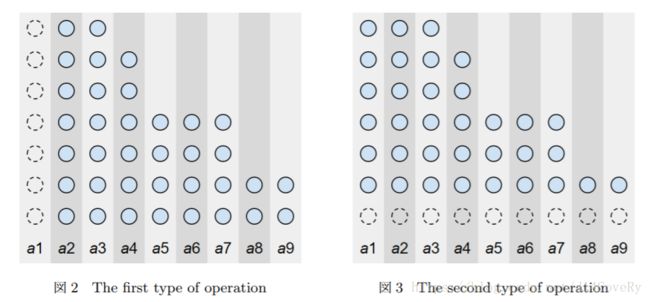
将操作看成一条路径：

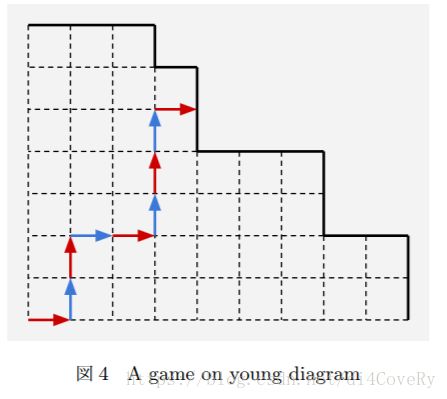
然后看一看每个点的胜负：

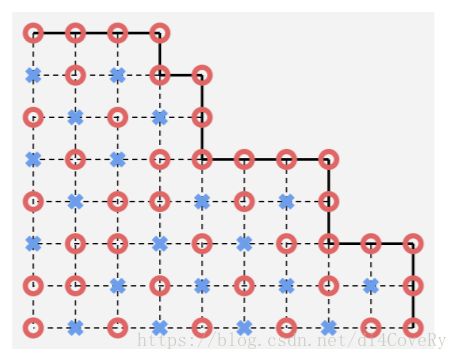
发现自左下向右上的对角线胜负关系相同

#include
#define N 500005
using namespace std;
int n,a[N],ans;
inline int rd() {   int r;scanf("%d",&r);return r;}
bool cmp(int p1,int p2) {return p1 > p2;}
int main(){
    n = rd();
    for (int i=1;i<=n;i++) a[i] = rd();
    sort(a+1,a+n+1,cmp);
    for(int i=1;i<=n;i++) if(i+1>a[i+1]) {
        for(int j=i+1;a[j]==i;j++) ans^=1;
        ans |= (a[i] - i) & 1;
        if (ans) puts("First"); else puts("Second");
        return 0;
    }
    return 0;
}