主席树【权值线段树】（转）

注：本文转自WCR神仙（应WCR本人要求）的博客，传送门：https://blog.csdn.net/g21wcr/article/details/82970228

一、权值线段树。

权值线段树，顾名思义，是建立在权值上的线段树。与普通的线段树不同【平时的线段树建立在定义域上，或者说位置下标上，比如说：一个1到n的序列，建立线段树后，根节点就存的是a[1]到a[n]的信息，根节点的左儿子就存的是a[1]到a[(1+n)/2]的信息，右儿子存的就是 a[(1+n)/2+1] 到a[n]的信息。】，权值线段树的叶子节点代表的是一个权值，而普通的线段树的叶子节点代表的是一个下标。

假如给定一个序列a[1]到a[n]，普通线段树的叶子节点代表的是位置i，可以存储额外信息，比如这个节点代表的区间内的数之和。而权值线段树的叶子节点代表的是某个权值i，它也可以存储额外信息，比如这个节点代表的权值区间内有多少个数，即：有多少个位置i，他们的权值在这个节点所代表的权值范围内。

【权值线段树相当于把普通线段树中位置（下标）与值的关系调换了过来】

二、经典问题。【区间查询第k小】

给定一个长度为n的数列ai，m次询问，每次询问给定l，r，k，求区间[l,r]第k小的数是多少。n、m≤2e5。【洛谷3834】

我们首先考虑一种解法：先把l到r排序，然后找到第k小就行了。但是每次拷贝再排序显然要超时。

【暴力做法】：

#include
using namespace std;
int a[200010],b[200010];
int n,m,l,r,k;
void read(int &x){
	x=0;char ch=getchar();
	while(ch>'9'||ch<'0') ch=getchar();
	while(ch<='9'&&ch>='0') x=(x<<3)+(x<<1)+ch-'0',ch=getchar();
}
int main(){
	read(n),read(m);
	for(int i=1;i<=n;++i)
		read(a[i]);
	for(int i=1;i<=m;++i){
		read(l),read(r),read(k);
		memcpy(b,a+l,(r-l+1)*4);//一个int占4个字节，所以要乘4
                //把a从l到r赋给b
		sort(b,b+r-l+1);
		printf("%d\n",b[k-1]);
	}
}

暴力居然能过五十分，暴力很重要啊。。

这时候就需要用到权值线段树来AC了！

【权值线段树做法】：

现在我们来考虑能不能预处理一些东西来求解。

先将所有数离散化。

离散化操作：

void disc_init(){
    sort(b+1,b+m+1);
    //先给数组排个序
    m=unique(b+1,b+m+1)-b-1;//注意是-b-1
    //再给数组去个重
    for(int i=1;i<=n;++i)
        a[i]=lower_bound(b+1,b+m+1,a[i])-b;
    //a[i]变成离散后的值
}

比如说一个序列有5个数：a[1]=5,a[2]=3,a[3]=4,a[4]=2,a[5]=2.-----①

排序后变成2,2,3,4,5.------②

去重后变成2,3,4,5，m为4.-----③

然后从1到n：原来的a[1]是5，现在变成了序列③中5的下标，就是4；3变成了去重后3的下标，现在就是2，以此类推，4变成3，2变成1【a[i]的值就变成了 把序列①排序后a[i]是第几小的数，2是第一小，就对应1，5是第四小，就对应4】

【这里不考虑重复的情况，比如：一个序列1,1,1,2,2,2，它的第一小，第二小，第三小，都是1，第四到第六小才是2】

那么这时候就把a[1]到a[5]离散化了：从5，3，4，2，2变成了4，2，3，1，1------④。

现在，离散后，我们这个序列的权值的值域就变为了[1,m]。这个地方的m为4。

 

 

我们本来的问题是查询区间[l,r]中的第k小。我们现在考虑一下二分答案。二分一个ans。根据[l,r]区间中小于等于ans的数的个数num来调整这个ans。如果num大于等于k，那么这个ans比真实答案要大，就要把ans缩小。否则，num小于k，就把ans放大。这个地方用权值线段树实现。

维护n颗权值线段树，第i颗权值线段树存储的是位置（下标）区间为[1,i]的信息。

在权值线段树，每个节点我们维护它所代表的权值区间内的数的个数。举个栗子吧：

序列a[1]到a[n]，离散后，值域变成了[1,m]。

假设第i颗权值线段树的根节点为root，则这棵权值线段树存的是a[1]到a[i]的信息。

root存权值为[1,m]的数的个数。

root的lc存权值为[1,(1+m)/2]的数的个数。

root的rc存权值为[(1+m)/2+1,m]的数的个数。

以此类推.........

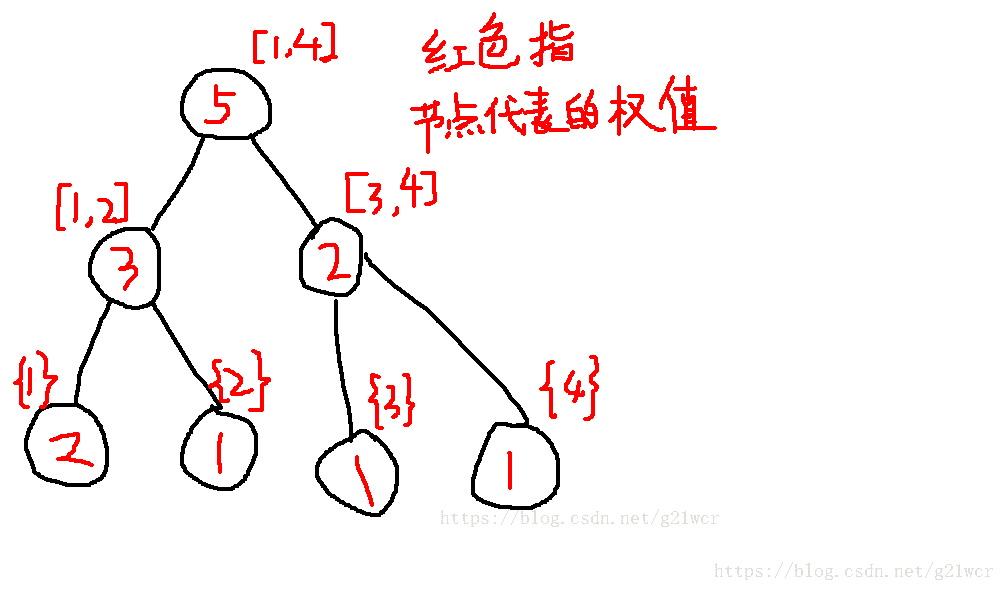
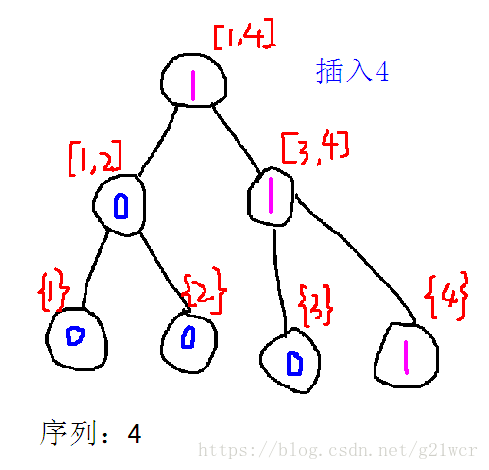
如下图为序列④构造出来的权值线段树。

 

现在我们查询区间l到r中有多少个数小于等于ans，即：询问有多少个数，下标在[l,r]之间且数的权值大小在[1,ans]（离散后）之间。假设第r颗权值线段树【维护a[1]到a[r]的信息】的[1,ans]这个区间内的数有cnt1个，第(l-1)颗权值线段树的[1,ans]这个区间的数有cnt2个，那么cnt1-cnt2就得到了a[l]到a[r]中小于等于ans的数的个数。

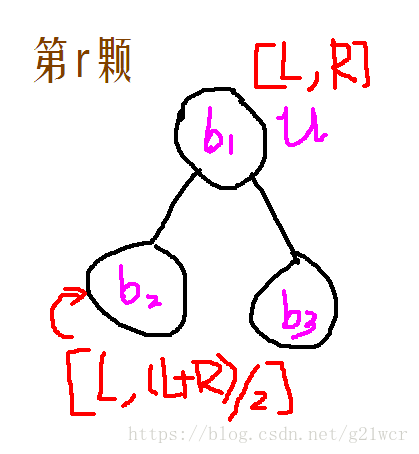
进一步，我们要求区间中的第k小数，记录一下第r颗和第(l-1)颗权值线段树的节点u、v，它们都代表着[L,R]的权值区间。然后根据这两个节点维护的数字个数sum，我们可以计算出a[l]到a[r]中，权值在区间[L,(L+R)/2]的数的个数——cnt=sum[lc[u]]-sum[lc[v]]。

那么这时cnt就是b2-a2.

对于第k小数，假如cnt≥k，说明答案在左子树中【小于等于ans的都不少于k个了，说明ans大了，要缩小ans。】，假如cnt＜k，说明答案在右子树中，且是右子树中的第k-cnt小元素【已经有cnt个数不大于ans了，还需要再有k-cnt个数不比ans大。把ans放大，把cnt变成k-cnt。】，我们可以递归下去求解。这个算法其实就是在权值线段树上二分。

那么现在考虑如何建出这n个权值线段树，显然不能全部直接建出来。

考虑相邻两个树的关系，它们只有一个数的区别。

第i颗树比第i-1颗树只多了i这个位置上的元素a[i]。那么实际上第i颗树与第i-1颗树之间只有log个节点的信息是不同的。

也就是说，我们在第i-1颗树上 插入一个节点a[i] 得到第i颗权值线段树，而单点插入过程中只会修改根到那个叶子节点的路径上的那log个节点。举个粒子吧：

还是看看序列④吧。

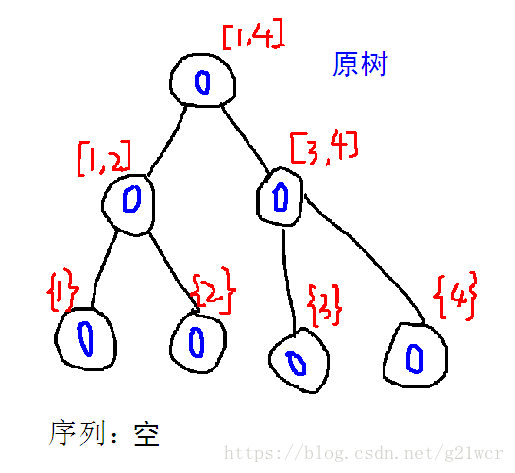
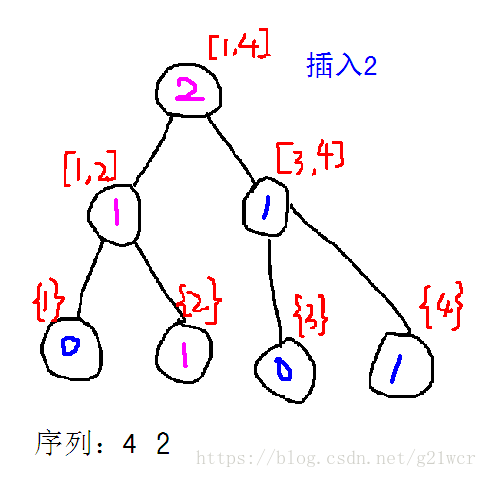
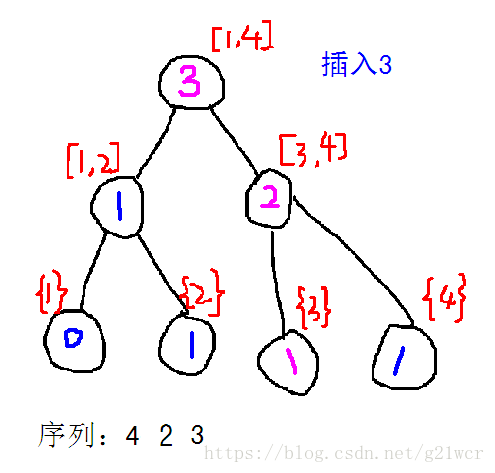
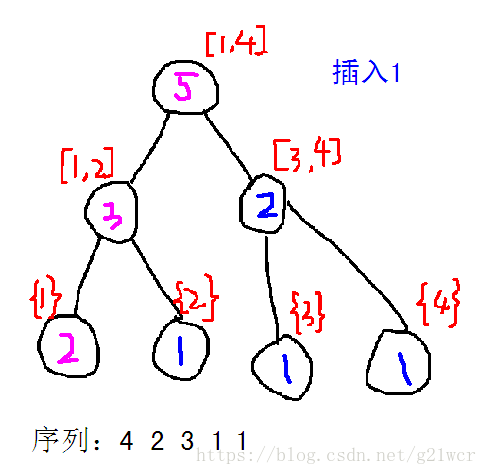
那么加数的过程大概是这样的——

粉色的部分是当前权值线段树相对于前一颗权值线段树不同的部分。

我们考虑一下插入的过程：先新建一个节点，表示第i颗树的根节点，接着从第i-1颗树以及第i颗树的根节点开始考虑。

假设插入的数是a[i]：如果a[i]的值在当前权值区间的左半部分，就新建一个左儿子，对应当前节点左儿子，然后当前节点的右儿子就指向前一个树的右儿子，因为它们的信息是完全相同的【结合图理解一下】。反之亦然。

那么插入一个点的时空复杂度都为O(log n),所以建立这颗主席树【权值线段树总体】的时空复杂度就是O(n log n),单次询问经过log n个节点，时间复杂度也为O(log n)，那么原问题我们就可以在O((n+m)*log n)的时间内解决了。

下面上代码吧：

//洛谷 P3834 可持久化线段树（主席树）
#include
#include
#include
using namespace std;
const int N=200005;
int n,m,q,t=0;
int a[N],b[N],root[N];
struct node
{
	int ls,rs,sum;
}tree[N*20];
void disc()
{
	int i;
	sort(b+1,b+n+1);
	m=unique(b+1,b+n+1)-(b+1);
	for(i=1;i<=n;++i)
	  a[i]=lower_bound(b+1,b+m+1,a[i])-b;
}

//insert函数就是说：当前插入的数p，会影响节点x，所以把x节点的sum加1.

//节点x代表一个权值区间，影响x就是说p在节点x所代表的权值区间内。
//那么先把前一个树的对应区间的节点复制过来，再加1，就行了。
//可以结合刚才的图感性理解一下。
void insert(int y,int &x,int l,int r,int p)
{
	x=++t;    //t相当于是一个节点的地址，每个节点是不同的。
	tree[x]=tree[y];    //复制前一个树的对应节点【它们代表的权值区间相同】。
	tree[x].sum++;      //给这个节点的sum加1.（这个1指的就是p）
	if(l==r)  return;   //搜索到根节点就返回。
	int mid=(l+r)>>1;

    //判断在哪个区间继续插入。
	if(p<=mid)  insert(tree[y].ls,tree[x].ls,l,mid,p);
	else  insert(tree[y].rs,tree[x].rs,mid+1,r,p);
}

//k是查询第k小
//x和y相当于是树的节点的地址。而l和r就是这两个节点的权值区间。
//一开始query(root[l-1],root[r],1,m,k)。
//root[l-1]就是第l-1颗树的根节点。root[r]就是第r颗树的根节点。
//比较它们左儿子代表的区间中的数的个数，差值为delta。根据delta判断这两个节点一起往哪个方向跳。
//分析过程和刚才二分的过程一样。
int query(int x,int y,int l,int r,int k)
{
	if(l==r)  return l;    //查到权值线段树的叶子节点就返回这个值。
	int delta=tree[tree[y].ls].sum-tree[tree[x].ls].sum;
	int mid=(l+r)>>1;
	if(k<=delta)  return query(tree[x].ls,tree[y].ls,l,mid,k);
	else  return query(tree[x].rs,tree[y].rs,mid+1,r,k-delta);
}
int main()
{
	int l,r,i,k;
	scanf("%d%d",&n,&q);
	for(i=1;i<=n;++i)
	{
		scanf("%d",&a[i]);
		b[i]=a[i];
	}
	disc();
	for(i=1;i<=n;++i)
	  insert(root[i-1],root[i],1,m,a[i]);
	for(i=1;i<=q;++i)
	{
		scanf("%d%d%d",&l,&r,&k);

        //query函数返回的是第k小的权值。
        //把这个权值转化为原来这个权值对应的数就行了。
		printf("%d\n",b[query(root[l-1],root[r],1,m,k)]);
	}
	return 0;
}

权值线段树差不多就这样了......【主席树】的本质就是一颗颗权值线段树，或者说一个权值线段树的前缀和。