KM算法详解+模板

 http://www.cnblogs.com/wenruo/p/5264235.html

KM算法用来求二分图最大权完美匹配。

本文配合该博文服用更佳：趣写算法系列之--匈牙利算法

 

 

现在有N男N女，男生和女生每两个人之间有好感度，我们希望把他们两两配对，并且最后希望好感度和最大。

怎么选择最优的配对方法呢？

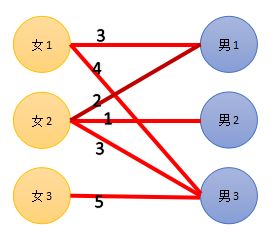
首先，每个妹子会有一个期望值，就是与她有好感度的男生中最大的好感度。男生呢，期望值为0，就是，，，只要有一个妹子就可以啦，不挑~~

这样，我们把每个人的期望值标出来。

然后，开始配对。配对方法：男女两人的期望和要等于两人之间的好感度。每一轮匹配，无论是否成功，每个男生只会被尝试匹配一次！

匹配过程：

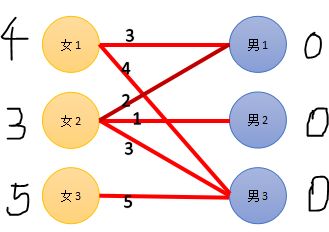
第一轮匹配：

============================

女1：选择了男3（此时女1--男3）

女2：也想选择男3，男3已经在该轮匹配过了，女2无其他合适选择，匹配失败。

===============================

这一轮参与匹配的人有：女1，女2，男3。

怎么办？？？很容易想到的，这两个女生只能降低一下期望值了，降低多少呢？两个妹子都在能选择的其他人中，也就是没参与这轮匹配的男生中，选择一个期望值降低的尽可能小的人。也就是再其他人中选择一个最合适的。

比如：女1选择男1，期望值要降低1。 女2选择男1，期望值要降低1。 女2选择男2，期望值要降低2。

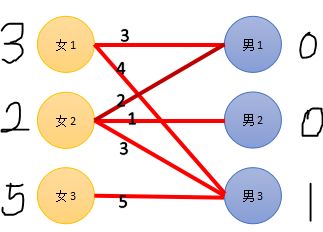
于是，只要期望值降低1，就有妹子可能选择其他人。所以妹子们的期望值要降低1点。

同时，刚才被抢的男生此时非常得意，因为有妹子来抢他，与是他的期望值提高了1点（就是同妹子们降低的期望值相同）。

与是期望值变成这样（当然，不参与刚才匹配过程的人期望值不变）

第二轮匹配：

============================

（女1已经在第一轮匹配完成了，女1--男3）

女2：选择男1。（此时女1--男3，女2--男1）

女3：选择男3，男3已经有女1了，于是女1尝试换人，换到男1，男1已经被在这一轮被尝试匹配过了。于是女1换人失败，这一轮匹配失败。

============================

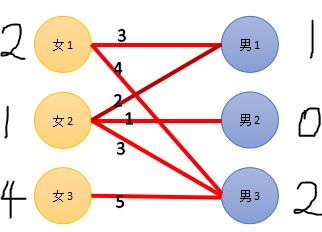
再一次改变期望值。

这次三个女生都参与了匹配，男1和男3参与匹配。女生尝试换人，于是期望值降低1。参与匹配的男生期望值增加1。

第三轮匹配：

============================

上一轮女1和女2是匹配完成的。（此时女1--男3，女2--男1）

女3：选择男3，男3的当前对象女1尝试换人，换到了男1，但是男1已经有女2了，于是女2再尝试换人，换到了男2，于是女2--男2，女1--男1，女3--男3

匹配成功！！！撒花~~

============================

虽然不停换人的过程听起来很麻烦，但其实整个是个递归的过程，实现起来比较简单。比较复杂的部分就是期望值的改变，但是可以在递归匹配的过程中顺带求出来。

 

模板（带详细注释）（入门题：HDU2255

#include 
#include 
#include 

using namespace std;
const int MAXN = 305;
const int INF = 0x3f3f3f3f;

int love[MAXN][MAXN];   // 记录每个妹子和每个男生的好感度
int ex_girl[MAXN];      // 每个妹子的期望值
int ex_boy[MAXN];       // 每个男生的期望值
bool vis_girl[MAXN];    // 记录每一轮匹配匹配过的女生
bool vis_boy[MAXN];     // 记录每一轮匹配匹配过的男生
int match[MAXN];        // 记录每个男生匹配到的妹子 如果没有则为-1
int slack[MAXN];        // 记录每个汉子如果能被妹子倾心最少还需要多少期望值

int N;


bool dfs(int girl)
{
    vis_girl[girl] = true;

    for (int boy = 0; boy < N; ++boy) {

        if (vis_boy[boy]) continue; // 每一轮匹配 每个男生只尝试一次

        int gap = ex_girl[girl] + ex_boy[boy] - love[girl][boy];

        if (gap == 0) {  // 如果符合要求
            vis_boy[boy] = true;
            if (match[boy] == -1 || dfs( match[boy] )) {    // 找到一个没有匹配的男生 或者该男生的妹子可以找到其他人
                match[boy] = girl;
                return true;
            }
        } else {
            slack[boy] = min(slack[boy], gap);  // slack 可以理解为该男生要得到女生的倾心 还需多少期望值 取最小值 备胎的样子【捂脸
        }
    }

    return false;
}

int KM()
{
    memset(match, -1, sizeof match);    // 初始每个男生都没有匹配的女生
    memset(ex_boy, 0, sizeof ex_boy);   // 初始每个男生的期望值为0

    // 每个女生的初始期望值是与她相连的男生最大的好感度
    for (int i = 0; i < N; ++i) {
        ex_girl[i] = love[i][0];
        for (int j = 1; j < N; ++j) {
            ex_girl[i] = max(ex_girl[i], love[i][j]);
        }
    }

    // 尝试为每一个女生解决归宿问题
    for (int i = 0; i < N; ++i) {

        fill(slack, slack + N, INF);    // 因为要取最小值 初始化为无穷大

        while (1) {
            // 为每个女生解决归宿问题的方法是 ：如果找不到就降低期望值，直到找到为止

            // 记录每轮匹配中男生女生是否被尝试匹配过
            memset(vis_girl, false, sizeof vis_girl);
            memset(vis_boy, false, sizeof vis_boy);

            if (dfs(i)) break;  // 找到归宿 退出

            // 如果不能找到 就降低期望值
            // 最小可降低的期望值
            int d = INF;
            for (int j = 0; j < N; ++j)
                if (!vis_boy[j]) d = min(d, slack[j]);

            for (int j = 0; j < N; ++j) {
                // 所有访问过的女生降低期望值
                if (vis_girl[j]) ex_girl[j] -= d;

                // 所有访问过的男生增加期望值
                if (vis_boy[j]) ex_boy[j] += d;
                // 没有访问过的boy 因为girl们的期望值降低，距离得到女生倾心又进了一步！
                else slack[j] -= d;
            }
        }
    }

    // 匹配完成 求出所有配对的好感度的和
    int res = 0;
    for (int i = 0; i < N; ++i)
        res += love[ match[i] ][i];

    return res;
}

int main()
{
    while (~scanf("%d", &N)) {

        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                scanf("%d", &love[i][j]);

        printf("%d\n", KM());
    }
    return 0;
}