【算法】有趣的二分图——一起来染色
我们定义一个二分图
如果我们能将一个图的节点集合分割成两个独立的子集A和B,并使图中的每一条边的两个节点一个来自A集合,一个来自B集合,我们就将这个图称为二分图。
请说人话!
在这个图中,一条边的两端节点,必须来自不同的集合。
换句话说,每个节点的邻居,必须是与它来自不同集合的。
集合一共有两个。
一张图就能说明白
二分图要求一条边的两个端点必须是属于两个不同的集合的:即邻居必须异色
目录
- 染色法概述
- 典型例题(母题)
- 典型例题(换壳题)
正文(★)
▊ 染色法概述
其实,上面的图解,就是一个染色的过程:
从任一顶点开始遍历整个连通域,遍历的过程中用两种不同的颜色(1,-1)对顶点进行染色,相邻顶点染成相反的颜色。
遍历过程中,会不断以某个节点为中心,扫描它的所有邻居:遇到未染色的邻居,就给它染上反色;遇到已经染色的邻居,就判断是否合法。
染色的记录是用一个染色数组draw[]实现的。
很显然,对于图的遍历,我们可以进行广度优先搜索和深度优先搜索(BFS / DFS)
▊ 母题
【判断二分图】
给定一个无向图graph,当这个图为二分图时返回true。
graph将会以邻接表方式给出,graph[i]表示图中与节点i相连的所有节点。
每个节点都是一个在0到graph.length-1之间的整数。这图中没有自环和平行边: graph[i] 中不存在i,并且graph[i]中没有重复的值。
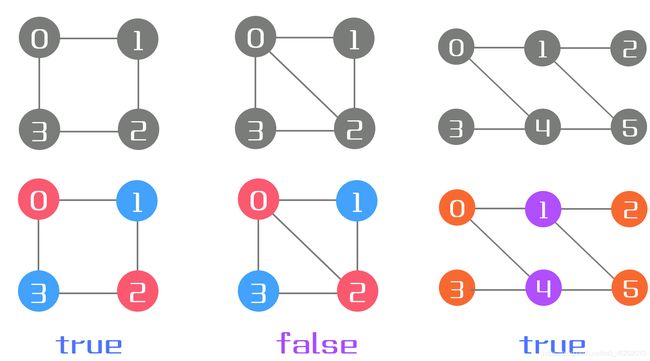
示例 1(上图1):
输入: [[1,3], [0,2], [1,3], [0,2]]
输出: true
示例 2(上图2):
输入: [[1,2,3], [0,2], [0,1,3], [0,2]]
输出: false
注意:
graph 的长度范围为 [1, 100]
graph[i] 中的元素的范围为 [0, graph.length - 1]
graph[i] 不会包含 i 或者有重复的值。
图是无向的: 如果j 在 graph[i]里边, 那么 i 也会在 graph[j]里边。
解法一 —— 染色法+BFS
class Solution {
/**
*【BFS】
* BFS经典思路:每次出队时,就判断出队节点的邻居是否被染色:
* 如果未被染色,就染成出队节点的反色
* 如果已经染色,就检查邻居的颜色是否合法,即与出队节点互为反色
*
*/
public boolean isBipartite(int[][] graph) {
int len = graph.length;
int[] draw = new int[len];
Queue<Integer> queue = new LinkedList<>();
for (int i = 0; i < len; i++) {
if(draw[i] != 0){
continue;
}
draw[i] = 1;
queue.offer(i);
while (!queue.isEmpty()) {
int index = queue.poll();
for (int node : graph[index]) {
if (draw[node] == 0) {
// 如果未被染色,就染成出队节点的反色;并入队
queue.offer(node);
draw[node] = -draw[index];
} else if(draw[node] == draw[index]) {
// 如果已经染色,就检查邻居的颜色是否合法
return false;
}
}
}
}
return true;
}
}
解法二 —— 染色法+DFS
class Solution {
/**
*【DFS】
* BFS返回一个boolean值,BFS的含义是:给当前节点(draw[index])染成color是否合法
* 如果已经染色,就检查是否是要涂的color
* 如果还未染色,就涂上color,并给其所有邻居尝试染上反色(递归)
*/
public boolean isBipartite(int[][] graph) {
int len = graph.length;
int[] draw = new int[len];
for(int i = 0; i < len; i++){
if(draw[i] == 0 && !DFS(graph, draw, i, 1)){
return false;
}
}
return true;
}
private boolean DFS(int[][] graph, int[] draw, int index, int color){
if(draw[index] != 0){
// 如果已经染色,就检查是否是要涂的color
return draw[index] == color;
}
draw[index] = color; // 如果还未染色,就涂上color,并给其所有邻居尝试染上反色(递归)
for(int node : graph[index]){
if(!DFS(graph, draw, node, -color)){
return false;
}
}
return true;
}
}
解法三(附赠 >_<) —— 并查集——敌人的敌人就是朋友
class Solution {
/**
*【并查集】
*
* 很有趣的思路:我们把一个节点的所有邻居合并到一个集合里————"敌人的敌人就是朋友"
*
* 代码思路:直接for遍历graph,每次遍历一个节点,以其为中心扫描邻居:
* 如果中心节点与邻居在同一集合,直接返回false
* 否则连接所有的邻居
*/
public boolean isBipartite(int[][] graph) {
int len = graph.length;
UnionSet unionSet = new UnionSet(len);
for (int i = 0; i < len; i++) {
int[] js = graph[i];
for (int j : js) {
if (unionSet.isUnion(i, j)) {
return false;
}
unionSet.union(j, js[0]);
}
}
return true;
}
}
class UnionSet {
int[] roots;
public UnionSet(int len) {
roots = new int[len];
for (int i = 0; i < len; i++) {
roots[i] = i;
}
}
public int findRoot(int node) {
// fintRoot寻找根节点是并查集的核心。
if (node == roots[node]) {
// 实际上这种递归写,寻找根节点的同时压缩了树的路径
return node;
}
roots[node] = findRoot(roots[node]);
return roots[node];
}
public boolean isUnion(int node1, int node2) {
return findRoot(node1) == findRoot(node2);
}
public void union(int node1, int node2) {
roots[node1] = findRoot(node2);
}
}
▊ 换壳题
【可能的二分法】
给定一组 N 人(编号为 1, 2, …, N), 我们想把每个人分进任意大小的两组。
每个人都可能不喜欢其他人,那么他们不应该属于同一组。
形式上,如果 dislikes[i] = [a, b],表示不允许将编号为 a 和 b 的人归入同一组。
当可以用这种方法将每个人分进两组时,返回 true;否则返回 false。
示例 1: 输入:N = 4, dislikes = [[1,2],[1,3],[2,4]] 输出:true
示例 2: 输入:N = 3, dislikes = [[1,2],[1,3],[2,3]] 输出:false
示例 3: 输入:N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]] 输出:false
>>> 两个互相不喜欢的人?
>>> 你会发现,这与"不和睦的邻居"是完全一类的问题————保证相邻节点不能同色。
>>>
>>> 可是,无论是"从某个点出发开始BFD/DFS整个图的染色法", 还是"将某个点的所有敌人都连接起来的并查集",用此时的dislikes数组,都是很难实现的
>>> 我们需要对dislikes数组进行处理————转换为邻接的形式。
>>> 下面给出两种转换方式:
List<Set<Integer>> list = new ArrayList<>();
for(int i = 0; i < N + 1; i++){
list.add(new HashSet<>());
}
for(int[] dislike : dislikes){
list.get(dislike[0]).add(dislike[1]);
list.get(dislike[1]).add(dislike[0]);
}
Map<Integer, List<Integer>> map = new HashMap<>();
for(int i = 0; i < N + 1; i++){
map.put(i, new ArrayList<>());
}
for(int[] dislike : dislikes){
map.get(dislike[0]).add(dislike[1]);
map.get(dislike[1]).add(dislike[0]);
}
// 因为学生编号从1开始,我们假设有一个0的同学————他谁都不讨厌。 他丝毫不会影响最终结果。理解一下。
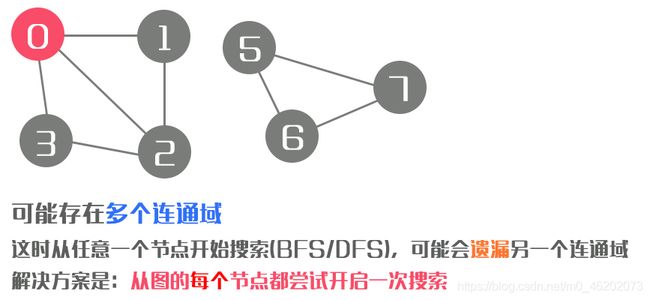
// 考虑到连通域不止一个的问题,BFS/DFS染色时依旧要从每个节点都尝试开始一次
☑ 部分题目来源 :
【 Leetcode Q785 】判断二分图
【 Leetcode Q886 】可能的二分法
♬ End
♪ By a Lolicon