『RMQ』解决RMQ问题的方法（一）—— 线段树

RMQ (Range Minimum/MaximumQuery)：
    对于长度为n的数组A，回答若干询问RMQ(A,i,j)(i,j<=n-1)，返回数组A中下标在i,j范围内的最小（大）值，也就是说，RMQ问题是指求区间最值的问题。

线段树是蒟蒻最先学的维护区间性质的数据结构，对于很多新手来说是很好的选择。写起来可以递归，非常的方便。
但最大的问题就是虽然说是O(nlogn)-O(logn)的时间复杂度中的常数比较大。实际运行效率并不是十分的好，不过一般的最值的问题还是基本可以解决的。

1.线段树前置知识：
    二叉树的建立与遍历算法
2.为什么引入线段树
    比如需要在1，7，3，4，2这5个数字中某段区间查找最小值，如1-5之间最小值是1，2-4之间最小是3，3-5之间最小是2等等，对于每次查询，我们可以在O(n)时间复杂度内处理，其中n是数字个数。如果有m次查询，那么整个问题时间复杂度是O(m*n)。如果有数字要修改呢？又得重新来过。这样的时间复杂度显然是无法满足我们的需求的，此时，就应当考虑线段树了

3.线段树的实质：
    线段树是一颗完全二叉树，为了轻量化，线段树使用结构体数组来存储。将结点化成线段：每个结点代表一个区间[L,R]。建树的时间是O（nlogn）
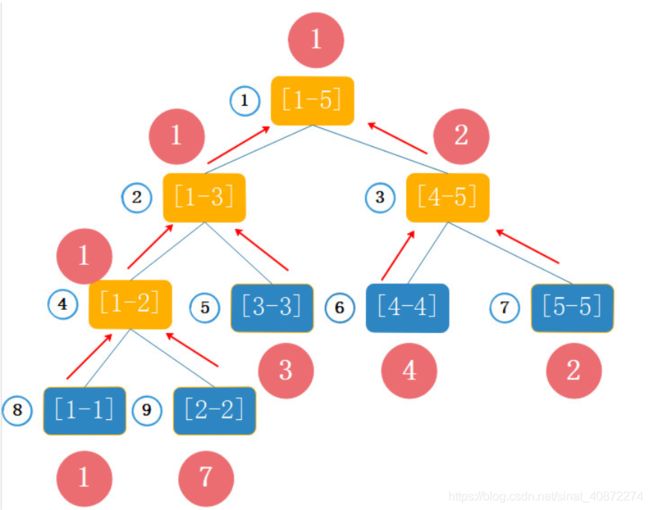
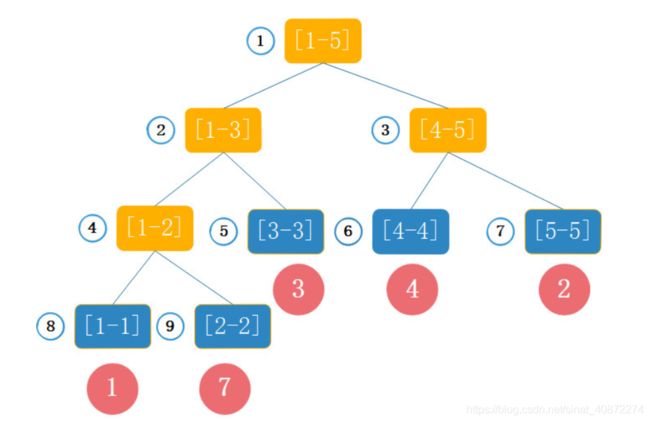下面以最小值为例，线段树中的每个结点有三个元素：L，R，min ，每次只需要递归左右子树的最小值，取一个最小的存在结点的min就可以了。查询的时间复杂度也是在O（nlogn）

信息学奥赛一本通：1541_【例 1】数列区间最大值
   题意：输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

代码：

#include 
#define ll long long
using namespace std;
const int Max = 1e5;
int n,m,maxx = 0;
struct Node {
	int l,r,max;
} st[4*Max];
int val[Max];
void creat(int l,int r,int root) {
	st[root].r = r;
	st[root].l = l;
	if(l == r) {
		st[root].max = val[l];
		return ;
	}
	int mid = (l+r)>>1;
	creat(l,mid,2*root);
	creat(mid+1,r,2*root+1);
	st[root].max = max(st[2*root].max,st[2*root+1].max);
}
void query(int l,int r,int root) {
	if(l == st[root].l && r == st[root].r) {
		maxx = max(st[root].max,maxx);
		return ;
	}
	int mid = (st[root].l + st[root].r)>>1;
	if(r <= mid) {
		query(l,r,2*root);
	} else if(l >= mid+1) {
		query(l,r,2*root+1);
	} else {
		query(l,mid,2*root);
		query(mid+1,r,2*root+1);
	}
}
int main() {
	scanf("%d %d",&n,&m);
	for(int i = 1; i <= n; i++)
		scanf("%d",val+i);
	creat(1,n,1);
	int l,r;
	for(int i = 0 ; i < m; i++) {
		maxx = 0;
		getchar();
		scanf("%d %d",&l,&r);
		query(l,r,1);
		printf("%d\n",maxx);
	}
	return 0;
}