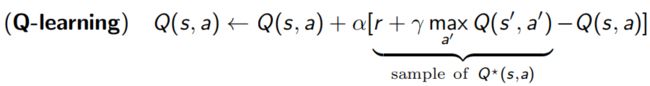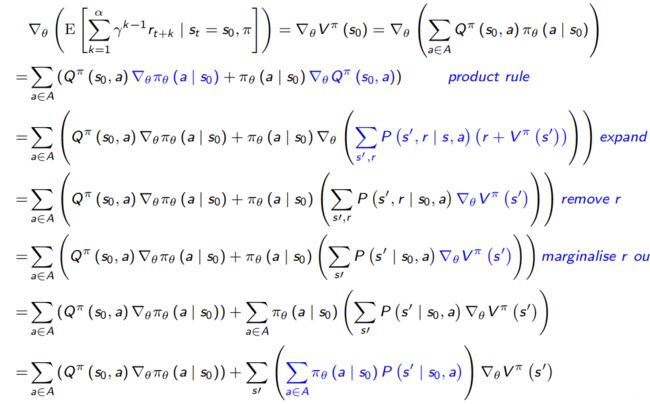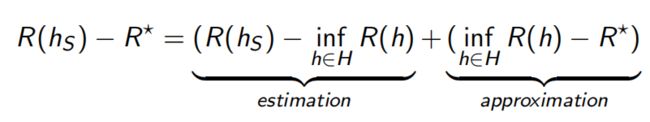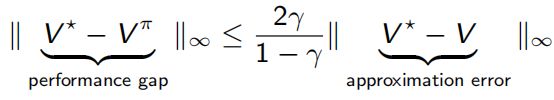【RLchina第二讲】 Foundations of Reinforcement Learning

  所有强化学习的方法无外乎两个近似的东西：

  一个是sample的性质，我们不可能把所有的state-action遍历，就有function approximation的方法。而近似的方法，会衍生出另外一个问题，sample complex的问题，需要多少数据能够达到什么样的一个精确程度。这个就是大部分理论分析的一个出发点。

策略方法

  policy有两种：1. deterministic policy $a:=\pi (s)$。2. randomized policy $p_r(a|s)=\pi (a|s)$。policy的目的是最大化奖励，奖励也有不同地定义形式：

1. total reward MDP over a finite horizon

$$J(\pi ):=\mathbb{E}\left[\sum _{k=0}^{N}R\left(s_k,\pi \left(s_k\right)\right)\right]$$

2. discounted reward MDP over an infinite horizon

$$J(\pi ):=\mathbb{E}\left[\sum _{k=0}^{\infty }{\gamma }^{k}R\left(s_k,\pi \left(s_k\right)\right)\right],\text{ for }0<\gamma <1$$

3. average reward MDP over an infinite horizon (ergodic reward)

$$J(\pi )=\underset{K\to \infty }{\lim }\mathbb{E}\left[\frac{1}{K+1}\sum _{k=0}^{K}R(s,\pi (s))\right]$$

想要获得这样的policy有两个核心的问题：

1. 怎么衡量policy的好坏？ (policy evaluation)

   policy evaluation value function: the expected discounted rewards under a policy $\pi$ starting from state $s$：

$$V^{\pi }(s):=\mathbb{E}\left[\sum _{k=0}^{\infty }{\gamma }^{k}R\left(s_k,\pi \left(s_k\right)\right)\mid s_0=s\right]$$

  and the corresponding action-value function (Q function), the expected reward of taking a particular action, under a policy

$$Q^{\pi }(s):=R(s,\pi (s))+{\mathbb{E}}_{s^{\prime }\sim \mathrm{Pr}\left(s^{\prime }\mid s,\pi (s)\right)}\left[V^{\star }\left(s^{\prime }\right)\right]$$

2. 最优的策略怎么获取？(policy optimisation)

  policy optimisation the value function optimising the policy gives the optimal value function,

$$V^{\star }(s):=\underset{\pi }{\max }\mathbb{E}\left[\sum _{k=0}^{\infty }R\left(s_k,\pi \left(s_k\right)\right)\mid s_0=s\right]$$

  By the same token, the optimal Q function is

$$Q^{\star }(s):=\underset{a}{\max }R(s,a)+{\mathbb{E}}_{s^{\prime }\sim \mathrm{Pr}\left(s^{\prime }\mid s,a\right)}\left[V^{\pi }\left(s^{\prime }\right)\right]$$

  如果知道state transition和reward function，我们就可以用DP的方法来做，如果是model-free的话，就用RL。值函数又可以分解为两部分，即时奖励和对下一个状态的估计。

$$\begin{array}{rl}{V}^{\pi }(s)& =\mathbb{E}\left[{\gamma }^{0}R\left(s_0,\pi \left(s_0\right)\right)\mid s_0=s\right]+\mathbb{E}\left[\sum _{k=1}^{\infty }{\gamma }^{k}R\left(s_k,\pi \left(s_k\right)\right)\mid s_0=s\right]\\ & =R(s,\pi (s))+{\mathbb{E}}_{s^{\prime }\sim \mathrm{Pr}\left(s^{\prime }\mid s,\pi (s)\right)}\left[\sum _{k=1}^{\infty }{\gamma }^{k}R\left(s_k,\pi \left(s_k\right)\right)\mid s_1=s^{\prime }\right]\\ & =R(s,\pi (s))+\gamma \sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,a\right)\mathbb{E}\left[\sum _{k=0}^{\infty }{\gamma }^{k}R\left(s_k,\pi \left(s_k\right)\right)\mid s_0=s^{\prime }\right]\end{array}$$

  最终可以得到策略$\pi$下的贝尔曼方程：

$$V^{\pi }(s)=R(s,\pi (s))+\gamma \sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,\pi (s)\right)V^{\pi }\left(s^{\prime }\right)$$

  已知转移概率$p_r(s^{\prime }|s,a)$和回报函数就可以迭代计算值函数：

  在值迭代的时候引入max，我们就间接引入了策略的求解，也成为贝尔曼最优方程：

$$V^{\star }(s)=\underset{a\in \mathbb{A}}{\max }R(s,a)+\gamma \sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,a\right)V^{\star }\left(s^{\prime }\right)$$

  由贝尔曼方程和贝尔曼最优方程衍生出了两种迭代算法，值迭代和策略迭代：

VI

  值迭代是最优策略下计算最优值函数$V^{\ast }$。有了最优的值函数，依据贝尔曼最优方程就可以计算得到最优策略：

$$a^{\star }={\pi }^{\star }(s)=\underset{a\in \mathbb{A}}{\mathrm{argmax}}R(s,a)+\gamma \sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,a\right)V^{\star }\left(s^{\prime }\right)$$

PI

  在策略迭代中，先计算某个策略下的值函数，收敛之后再去求新的policy。

VI and PI: 收敛性分析

  在求证VI和PI的收敛性分析的时候有一个很重要的工具operator，贝尔曼方程或者贝尔曼最优方程可以用operator来表示：

$$\begin{array}{rl}{T}^{\pi }V(s)& :=R(s,a)+\gamma \sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,a\right)V\left(s^{\prime }\right),\forall s\\ TV(s)& :=\underset{a\in \mathbb{A}}{\max }R(s,a)+\gamma \sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,a\right)V\left(s^{\prime }\right)\forall s\end{array}$$

  operator是function到function的映射，可以将值函数$V(s)$转成另外一个函数$TV(s)$。这种映射满足两点性质：

1. monotonicity(单调)：如果对任意$s$,有$V(s)\ge U(s)$，那么：

$$\begin{array}{c}{T}^{\pi }V(s)\ge T^{\pi }U(s)\\ TV(s)\ge TU(s)\end{array}$$

• 单调性证明：

  由$T^{\pi }V(s)\ge T^{\pi }U(s)$可知：

$$T^{\pi }V(s)-T^{\pi }U(s)=\sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,\pi (s)\right)\left(V\left(s^{\prime }\right)-U\left(s^{\prime }\right)\right)\ge 0$$

  由$T^{\pi }V(s)$的定义，将其展开即可得到：

$$R(s,a)+\sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,a\right)V\left(s^{\prime }\right)\ge R(s,a)+\sum _{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,a\right)U\left(s^{\prime }\right)$$

2. contraction(收缩)：

$$\begin{array}{rl}{\Vert T^{\pi }V-T^{\pi }U\Vert }_{\infty }& \le \gamma \Vert V-U{\Vert }_{\infty }\\ \Vert TV-TU{\Vert }_{\infty }& \le \gamma \Vert V-U{\Vert }_{\infty }\end{array}$$

  从原空间到映射空间，两点之间的距离是收缩的。收缩的约束是折扣因子$\gamma$，假设其中一个值函数是最优的，那么他们就会越来越近。

• 压缩映射证明：

  ${\Vert T^{\pi }V-T^{\pi }U\Vert }_{\infty }\le \gamma \Vert V-U{\Vert }_{\infty }$展开有：

$$\begin{array}{c}{\Vert T^{\pi }V-T^{\pi }U\Vert }_{\infty }={\max }_s\gamma {\sum }_{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,\pi (s)\right)\left|V\left(s^{\prime }\right)-U\left(s^{\prime }\right)\right|\\ \le \gamma \left({\sum }_{s^{\prime }}\mathrm{Pr}\left(s^{\prime }\mid s,\pi (s)\right)\right){\max }_{s^{\prime }}\left|V\left(s^{\prime }\right)-U\left(s^{\prime }\right)\right|\le \gamma \Vert U-V{\Vert }_{\infty }\end{array}$$

  $\Vert TV-TU{\Vert }_{\infty }\le \gamma \Vert V-U{\Vert }_{\infty }$展开有：

  对任意一个contraction operator，我们都有一个唯一的不动点$V^{\ast }=T{V}^{\ast }$。有一个不动点，然后另外一个点不断地靠近它，然后就收敛到这个不动点。

$$\begin{array}{r}{\Vert v_{k+1}-v^{\star }\Vert }_{\infty }={\Vert T{V}_k-T{V}^{\star }\Vert }_{\infty }\\ \le \gamma {\Vert V_k-V^{\star }\Vert }_{\infty }\le \cdots \le {\gamma }^{k+1}{\Vert V_0-V^{\star }\Vert }_{\infty }\to 0\end{array}$$

  有了这两个性质之后就可以证明策略迭代的收敛性：

  假设我们有了新的策略${\pi }_{k+1}$(下标表示在k+1的策略下迭代)，用这个新的策略来更新值函数，依据贝尔曼方程有：

$$\begin{array}{rl}{V}^{{\pi }_{k+1}}& ={\left(I-\gamma P^{\pi k+1}\right)}^{-1}{R}^{{\pi }_{k+1}}\\ & \ge {\left(I-\gamma P^{{\pi }_{k+1}}\right)}^{-1}\left(V^{{\pi }_k}-\gamma P^{{\pi }_{k+1}}{V}^{{\pi }_k}\right)\\ & =V^{{\pi }_{\circ }1d}\end{array}$$

  上述的不等号由以下公式推导得到($T{V}^{{\pi }_k}$为最优贝尔曼方程)：

$$\begin{array}{rl}{R}^{{\pi }_{k+1}}+\gamma P^{{\pi }_{k+1}}{V}^{{\pi }_k}& =T^{{\pi }_{k+1}}{V}^{{\pi }_k}=T{V}^{{\pi }_k}\ge V^{{\pi }_k}\\ & ⟺R^{{\pi }_{k+1}}\ge \left(I-\gamma P^{{\pi }_{k+1}}\right)V^{{\pi }_k}\end{array}$$

  因为值函数是单调的，所以有$V^{{\pi }^{\star }}={\lim }_{k\to \infty }{V}^{{\pi }_k}$，存在$V^{{\pi }^{\star }}=T{V}^{{\pi }^{\star }}$满足贝尔曼最优方程。

  VI and PI的问题：1. 没法解决连续状态-动作空间的问题。也存在维度灾难问题。2. POMDP问题不可解。3. Unknown model的问题不可解。

Q learning

  对于不知道reward，也不知道转移概率的情况，Q-Learning采用sample数据的方式来做值函数的更新：

小结：

  RL就是在MDP的约束下求解策略$\pi$，VI/PI的方法会遇到维度灾难的问题。然后通过值函数近似(function approximate)，或者sample的方法，像TD/MC的方法。function的估计可以泛化到未知的state，也正是由这些问题导致converge的算法变得不converge。对于PI的方法，就是对策略$\pi$用function来近似。

n-step transition probability: an example

  当马尔可夫链的状态转移概率在long-term下固定了，称其具有stationary distribution：

  在满足两个条件的情况下，马尔科夫链会具有stationary distribution的性质：

1. 任意一个state都具有一个path到另外一个state。
2. 不允许有loop的情况，就是不能在一个state圈里面转。

  回到PI的目标函数上来，假定策略${\pi }_{\theta }$，这个策略的期望回报可表示为：

$$J(\theta )=\sum _{s\in S}{d}^{\pi }(s)V^{\pi }(s)=\sum _{s\in S}{d}^{\pi }(s)\left(\sum _{a\in A}{\pi }_{\theta }(a\mid s)Q^{\pi }(s,a)\right)$$

  其中$d^{\pi }(s):={\lim }_{t\to \infty }p\left(S_t=s\mid s_0,{\pi }_{\theta }\right)$，是stationary distribution的话，那这个策略的评估是与初始状态无关的，因此在$J(\theta )$中就不需要$s_0$。

  对于$J(\theta )$的目标函数，我们就可以用gradient的方法来做，但是这个参数$\theta$的求解比较trick，因为它影响两个东西：

1. 动作的选择${\pi }_{\theta }(a|s)$。
2. stationary distribution $d^{\pi }$，因为$p(s^{\prime }|s)=p(s^{\prime }|s,a)$。

  这样的话求解就比较麻烦了，99年Sutton提出了下面这篇论文：

• Richard S Sutton et al. “Policy gradient methods for reinforcement learning with function approximation”. In: Advances in Neural Information Processing Systems (NeurIPS). 1999, pp. 1057–1063.

  去消去state distribution的求导问题：

  因此得到了对${\nabla }_{\theta }{V}^{\pi }\left(s_0\right)$的求导也变成了循环(recursive)的形式：

$$\begin{array}{rl}{\nabla }_{\theta }{V}^{\pi }\left(s_0\right)=& \sum _{a\in A}\left(Q^{\pi }\left(s_0,a\right){\nabla }_{\theta }{\pi }_{\theta }\left(a\mid s_0\right)\right)\\ & +\sum _{s\prime }\left(\sum _{a\in A}{\pi }_{\theta }\left(a\mid s_0\right)P\left(s^{\prime }\mid s_0,a\right)\right){\nabla }_{\theta }{V}^{\pi }\left(s^{\prime }\right)\end{array}$$

  简单化之后得到：

$${\nabla }_{\theta }{V}^{\pi }\left(s_0\right)=\phi \left(s_0\right)+\sum _{s^{\prime }}{P}^{\pi }\left(s^{\prime }\mid s_0\right){\nabla }_{\theta }{V}^{\pi }\left(s^{\prime }\right)$$

  其中$\phi \left(s_0\right):={\sum }_{a\in A}\left(Q^{\pi }\left(s_0,a\right){\nabla }_{\theta }{\pi }_{\theta }\left(a\mid s_0\right)\right)$， Markov transition表示成$P^{\pi }\left(s^{\prime }\mid s_0\right):={\sum }_{a\in A}{\pi }_{\theta }\left(a\mid s_0\right)P\left(s^{\prime }\mid s_0,a\right)$形式。

  定义从$s_0$状态转移k步，关系如下：

$$P^{\pi }\left(s^{\prime \prime }\mid s_0,k\right)\equiv \sum _{s^{\prime }}{P}^{\pi }\left(s^{\prime \prime }\mid s^{\prime },k-1\right)P^{\pi }\left(s^{\prime }\mid s_0\right)$$

  回到之前的循环形式：

  再定义$d^{\pi }(s):={\sum }_{k=0}^{\alpha }{P}^{\pi }\left(s\mid s_0,k\right)$，那此时就与之前stationary distribution一样了，可以写成：

$${\nabla }_{\theta }{V}^{\pi }\left(s_0\right)=\sum _{s\in S}{d}^{\pi }(s)\sum _{a\in A}\left(Q^{\pi }(s,a){\nabla }_{\theta }{\pi }_{\theta }(a\mid s)\right)$$

  也就是梯度也是recursive的形式。这样使得求梯度的时候不用考虑状态转移。另外一点是上式中${\sum }_{a\in A}$是对所有的动作求和，但是我们是sample样本，那怎么使得我们的estimation是unbiased的呢？

$$\begin{array}{c}{\nabla }_{\theta }{V}^{\pi }\left(s_0\right)={\sum }_{s\in S}{d}^{\pi }(s){\sum }_{a\in A}\left(Q^{\pi }(s,a){\nabla }_{\theta }{\pi }_{\theta }(a\mid s)\right)\\ \propto {\sum }_{s\in S}\mu (s){\sum }_{a\in A}\left({\pi }_{\theta }(a\mid s)Q^{\pi }(s,a)\frac{{\nabla }_{\theta }{\pi }_{\theta }(a\mid s)}{{\pi }_{\theta }(a\mid s)}\right)\\ =E_{s\sim \mu ,a\sim \pi }\left[Q^{\pi }(s,a){\nabla }_{\theta }\ln {\pi }_{\theta }(a\mid s)\right]\\ =E_{s\sim \mu ,a\sim \pi }\left[G_t{\nabla }_{\theta }\ln {\pi }_{\theta }(a\mid s)\right]\\ \text{ where }{E}_{s\sim d\pi ,a\sim \pi }\left[G_t\mid s,a\right]=Q^{\pi }(s,a)\end{array}$$

  乘一个${\pi }_{\theta }(a\mid s)$，使其概率化，来解决这一点。此时梯度更新变为：

$${\theta }_{t+1}={\theta }_t+\alpha G_t{\nabla }_{\theta }\ln {\pi }_{\theta }(a\mid s)$$

• Ronald J Williams. “Simple statistical gradient-following algorithms for connectionist reinforcement learning”. In: Machine learning 8.3-4 (1992).
  

  但是如果sample到episode结束的话，这个variance就会比较大，一般我们加个baseline$V^{{\pi }_{\theta }}(s)$来减少方差：

$$A^{{\pi }_{\theta }}(s,a):=Q^{{\pi }_{\theta }}(s,a)-V^{{\pi }_{\theta }}(s)$$

Computational learning theory

  在q-learning和pg的方法中都是通过sample来做的，那learnability怎么衡量呢，也就是sample的数量对收敛性的影响。

Probably Approximately Correct (PAC) learning

  PAC主要关注两点，sample complexity和computational complexity。这里我们主要关注sample complexity。

• PAC定义：

  因为$S$是sample自distribution$D$，所以定义一下误差：

理论分析

• PAC Learning定义：

  PAC Learning大概的意思就是找一个算法，使得其在样本上的误差(与generalisation error之间的误差)，以一个很高的概率去小于一个值：

Learning bound for finite H - consistent case：

  那$\epsilon$和$m$、$\delta$的关系是什么呢？

  证明：

  上述是consistent case的情况，也就是我们能够找到训练误差为0的假设，但很多时候做不到这一点，这个时候我们就需要其它的一些方法。

Learning bound for finite H: inconsistent Case

   inconsistent hypotheses就是会在training set上存在些许误差，这个时候我们利用Hoeffding’s inequality来解决这个问题：

• Hoeffding’s inequality

  与之前类似，其定理和证明可表示为：

  这里有一个概念，估计误差和近似误差。在训练集$s$上的学到的假设为$h_s$，那与真实的误差$R^{\ast }$之间的差距可以表示为两部分：

  一个是sample数量有限导致的error(estimation error)，另外一个是假设空间$H$本身导致的误差(approximation error)。这两个误差一个是sample导致的，另外一个是做approximate所导致的，由此有了上述的这些bound，有了这个bound之后我们就可以去分析各种各样的算法。

Theoretical analysis

  先来分析approximation error，当状态空间很大时，我们可以用线性模型或者神经网络来逼近这个值函数，这种方法也被称作(Approximate DP)，我们希望在整个函数空间$\mathcal{V}$中找到一个$V$不断逼近最优值函数$V^{\ast }$：

$$V=\underset{U\in \mathcal{V}}{\mathrm{argmin}}\mathrm{distance}\left(V^{\star },U\right)$$

  若得到$V$就可以利用贪婪策略得到强化的策略。现如今的大部分RL算法都是在ADP的基础上做状态转移和奖励未知的情况，一般也都是用sample来做。此时性能上面的gap与近似误差的关系可表示为：

• ADP performance bounds

  因为用的贪婪策略$T^{\pi }=T$。

• Bounds by Bellman residual

  上述也是用的贪婪策略。这样就把寻找与最优值函数$V^{\ast }$(这个值未知)的差距转化为寻找Bellman residua的差距，像TD就是这么做的。接下来就是对 Bellman residual minimisation：

• Bellman residual minimisation：

$$(\text{ BRM })\underset{V\in \mathcal{V}}{\min }\Vert TV-V\Vert$$

Performance bounds of AVI(值迭代的bound)

  AVI bound [BT96]: K次迭代的bound结果：

$$\begin{array}{rl}{\Vert V^{\star }-V^{{\pi }_K}\Vert }_{\infty }\le \frac{2\gamma }{(1-\gamma {)}^2}& \underset{0\le k\le K}{\max }{\Vert T{V}_k-V_{k+1}\Vert }_{\infty }\\ & +\frac{2{\gamma }^{K+1}}{1-\gamma }{\Vert V^{\star }-V_0\Vert }_{\infty }\end{array}$$

证明：

令$\epsilon ={\max }_{0\le k\le K}{\Vert T{V}_k-V_{k+1}\Vert }_{\infty }$，有：

$$\begin{array}{rl}{\Vert V^{\star }-V_{k+1}\Vert }_{\infty }& \le \Vert T{V}^{\star }-T{V}_k\Vert +{\Vert T{V}_k-V_{k+1}\Vert }_{\infty }\\ & \le \gamma {\Vert V^{\star }-V_k\Vert }_{\infty }+\epsilon \end{array}$$

将上述结果迭代下去有：

$$\begin{array}{rl}{\Vert V^{\star }-V_k\Vert }_{\infty }& \le \left(1+\gamma +\cdots +{\gamma }^{K-1}\right)\epsilon +{\gamma }^K{\Vert V^{\star }-V_0\Vert }_{\infty }\\ & \le \frac{1}{1-\gamma }\epsilon +{\gamma }^K{\Vert V^{\star }-V_0\Vert }_{\infty }\end{array}$$

把这个结果带入到公式13即可得证。

下文并未看懂，以后再补：

Performance bounds of API(策略迭代的bound)

• API bound [BT96]: the asymptotic performance bound is

$$\underset{k\to \infty }{\mathrm{limsup}}{\Vert V^{\star }-V^{{\pi }_k}\Vert }_{\infty }\le \frac{2\gamma }{(1-\gamma {)}^2}\underset{k\to \infty }{\mathrm{limsup}}{\Vert V_k-V^{{\pi }_k}\Vert }_{\infty }$$

证明：

Performance bounds of BRM

Sample-based ADP: sample complexity

• Sample complexity: sampling-based AVI

• Deep Q learning and its sample complexity