winer_bamboo
winer_bamboo

P2756 飞行员配对方案问题 （最大流-二分图最大匹配）

题目来源

P2762 太空飞行计划问题

题目分析

中文题，题意就不用说了吧...

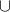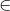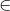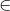思路：经典二分图匹配问题，我们记M表示外籍飞行员的顶点集合，用N表示英国飞行员的顶点集合，E表示匹配关系，二分图G = (M\cupN,E)，则对于任意的 m \inM，n\inN, 外籍飞行员m和英国飞行员n匹配\Leftrightarrow(m,n) \in E

而G中满足两两不含公共端点的变的集合K\subseteqE的基数|K|的最大值 ，就是我们需要求的最大匹配数（题目求的是最大匹配数的两倍）

我们可以将二分图最大匹配问题看成是一种特殊的最大流问题，建图过程如下：

将原图中所有的无向边e改成有向边，方向为从M到N，容量为1。增加源点s和汇点t，从s向M中每个点连一条容量为1的边，从N中每个点向t连一条容量为1的边。

这样一来，我们构建的图G'中最大的s-t流的流量就是原来二分图G中的最大匹配的匹配数了。

下图为第一个样例的图，蓝线代表容量为1的边（未修改之前），红边组成增广路径。

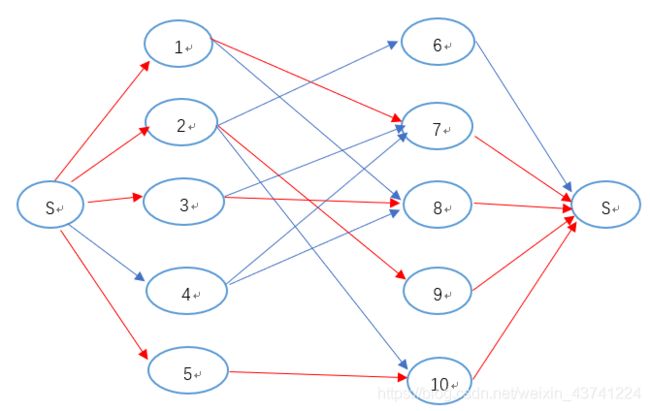
P2756 飞行员配对方案问题 （最大流-二分图最大匹配）_第1张图片

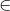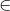求出了最大匹配，我们还需要知道哪些顶点是匹配的，借助上图，我们注意到如果最终在残余网络中有边 e (m,n) 的容量为0， m \inM，n\inN，那么 m,n为一个匹配，所以我们枚举M,N之间每一条边来得出答案。

代码区

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include 
#include 
#define bug cout << "**********" << endl
#define show(x,y) cout<<"["<q;
	q.push(s);
	while (!q.empty())
	{
		int u = q.front();q.pop();
		for (int i = head[u]; i != -1;i = edge[i].next)
		{
			int v = edge[i].to;
			if (dis[v] == -1 && edge[i].flow > 0)
			{
				dis[v] = dis[u] + 1;
				if (v == t) return true;
				q.push(v);
			}
		}
	}
	return false;
}

int dfs(int u, int flow_in)
{
	if (u == t) return flow_in;
	int flow_out = 0;
	for (int i = head[u]; i != -1;i = edge[i].next)
	{
		int v = edge[i].to;
		if (dis[v] == dis[u] + 1 && edge[i].flow > 0)
		{
			int flow_part = dfs(v, min(flow_in, edge[i].flow));
			if (flow_part == 0) continue;
			flow_in -= flow_part;
			flow_out += flow_part;
			edge[i].flow -= flow_part;
			edge[i ^ 1].flow += flow_part;
			if (flow_in == 0)break;
		}
	}
	return flow_out;
}

int max_val()
{
	int sum = 0;
	while (bfs())
	{
		sum += dfs(s, inf);
	}
	return sum;
}

int main()
{
#ifdef LOCAL
	freopen("input.txt", "r", stdin);
	freopen("output.txt", "w", stdout);
#endif
	while (scanf("%d%d", &m, &n) != EOF)
	{
		init();
		s = 0, t = n + 1;
		for (int i = 1;i <= m;i++)
		{
			add(s, i, 1);add(i, s, 0);	//由源点向外籍飞行员建边
		}
		for (int i = m + 1; i <= n;i++)
		{
			add(i, t, 1);add(t, i, 0);
		}
		while (scanf("%d%d", &a, &b) != EOF && a != -1 && b != -1)
		{
			add(a, b, 1);add(b, a, 0);
		}
		printf("%d\n", max_val());
		for (int u = 1;u <= m;u++)
		{
			for (int i = head[u]; i != -1;i = edge[i].next)
			{
				if (edge[i].flow == 0 && edge[i].to != s && edge[i].to != t)
				{
					printf("%d %d\n", u, edge[i].to);
				}
			}
		}
	}
	return 0;
}

 

你可能感兴趣的:(网络流)

  • 流量牵引技术与传统防火墙的区别 666IDCaaa ddos
    在网络安全领域，流量牵引技术和传统防火墙都起着重要的作用，但它们在很多方面存在着明显的区别。一、工作原理不同传统防火墙主要是通过设置访问控制规则来过滤网络流量。它基于预先设定的策略，对进入和离开网络的数据包进行检查，根据源地址、目的地址、端口号等信息决定是否允许数据包通过。例如，企业可以设置防火墙规则，只允许特定IP地址的设备访问内部网络资源，或者禁止某些端口的流量进入，以防止潜在的攻击。而流量牵
  • 面对容貌焦虑，请与自己和解 Alin曾玲
    容貌焦虑，网络流行词，是指在放大颜值作用的环境下，很多人对于自己的外貌不够自信。关于“容貌焦虑”这个词，也许是随着年龄的增长，越发能体会到这个容貌焦虑的心情。岁月留下的眼纹、颈纹、下垂的苹果肌，失去灵动的双眼，还有生完小孩以后走形的身材等等。于是，越来越多的轻医美走进了我们的心底。其实在能力范围内若是能做一些后天的保养来延缓衰老的速度，我也是认可的。可若是盲目的一味追求外在完美，而忽视了内在的修行
  • python绝技运用python成为顶级pdf_python绝技：运用python成为顶级黑客 中文pdf完整版[42MB]... weixin_39851261
    Python是一门常用的编程语言，它不仅上手容易，而且还拥有丰富的支持库。对经常需要针对自己所处的特定场景编写专用工具的黑客、计算机犯罪调查人员、渗透测试师和安全工程师来说，Python的这些特点可以帮助他们又快又好地完成这一任务，以极少的代码量实现所需的功能。Python绝技：运用Python成为顶级黑客结合具体的场景和真实的案例，详述了Python在渗透测试、电子取证、网络流量分析、无线安全、
  • C# 网口通信（通过Sockets类） 萨达大 c#服务器网络网口通讯上位机
    文章目录1.引入Sockets2.定义TcpClient3.连接网口4.发送数据5.关闭连接1.引入SocketsusingSystem.Net.Sockets;2.定义TcpClientprivateTcpClienttcpClient;//TcpClient实例privateNetworkStreamstream;//网络流，用于与服务器通信3.连接网口tcpClient=newTcpClie
  • 日更文40 知足常乐 樱祷
    累么？累…累就对，舒服是留给死人的！无意间发现这句话，这好像是好长时间的网络流行语了。在这个社会里，人活着没有太舒服的。小时候期盼长大，长大了怀念小时候。人也是很不容易满足的。昨天无意间看了一篇文章，关于爱情的，关于婚姻的。婚姻是需要真心经营的，是的。妻子要和丈夫离婚，丈夫不想离婚，找来人调解。调解人问到妻子，为什么要离婚？妻子说：他不上进，没胆识。调解人又问，你当初为什么嫁给他？妻子回：因为他老
  • 《520表白日》 去看看陌生的风景
    随着网络科技的发达，网络信息也时刻给网民洗脑，传染情绪，网络的情绪状态具有传染性，人们只要接触到他人的情绪，就会在毫无察觉的状态下受其影响，转向这种主流情绪。今天是520日，各大群，私聊都是讨论520日，又或者发祝福图片、发红包、又或者用最温暖、最甜的文字向对方表达。不知道从什么时候起520日成为了网络流行的日子，520日适合亲情表白、也适合夫妻间、好朋友间、闺蜜间、师生情、更适合年轻情侣……或许
  • 叶华芳随笔第1217篇： 叶华芳随笔
    2022/05/16星期一，农历四月十六【离农历新年还有260天，今天是2022年的第130天】叶华芳随笔第1217篇：这辈子吃不上四个菜，网络流行语，意思就是：你结不了婚，你孩子满不了月，你死的时候没人在乎你，死了没人祭奠你。所以不要骂别人说：你这辈子都吃不上四个菜，这是最恶毒的咒语。吃什么不重要，重要的是和谁吃。所以有时候一个人或是一群人吃饭都不是一件很开心的事情。今天去我家河边走路了，一河两
  • 话说“松弛感” 熊更姣
    熊更姣焦点解决学习分享第160天（约练69次30咨15来18观6学）今天晨读的时候，张艳萍老师提到了一个现在的网络流行词“松弛感”，建议我们可以讨论一下这个话题。当时，也许是一种心理投射，我对松弛感的理解，以为就是一种松懈的感觉，主要是因为最近我感觉自己的学习，有了一些松懈的表现，所以，当张老师提到松弛感的时候。我就想到了松懈这样的一个含义。但实际上，“松弛感”是现在网络上谈论得比较多的一个词语，
  • 速盾：中秋节使用cdn的企业多吗？ 速盾cdn 前端数据库运维
    中秋节是中国传统的重要节日之一，人们会通过各种方式来庆祝这一节日，包括赏月、吃月饼、团圆等。在这个期间，各个行业都会做出相关的准备来迎接节日的到来，其中包括使用CDN加速技术的企业。CDN，即内容分发网络，是一种通过将内容分发到全球分布的服务器上，以提高用户访问速度和服务质量的技术。在中秋节期间，由于节日的特殊性，各个企业在推出相关促销活动、提供特色服务等方面都会增加网络流量和访问量。为了应对这种
  • linux运维常见命令行 问道飞鱼 运维linux服务器
    文章目录用户管理创建用户修改用户信息列出用户信息添加用户到组删除用户创建和管理组查看用户和组的信息其他相关命令文件管理文件和目录的基本操作文件权限管理文件压缩和归档磁盘管理查看磁盘使用情况查看文件和目录的磁盘使用情况磁盘分区管理挂载和卸载文件系统磁盘配额管理LVM（LogicalVolumeManager）管理网络管理查看网络接口状态配置网络接口查看和管理路由表管理DNS和主机名网络诊断工具网络流
  • 推荐开源项目：Luci-App-BandwidthD —— 网络流量监控利器 毕艾琳
    推荐开源项目：Luci-App-BandwidthD——网络流量监控利器项目简介是一个基于OpenWrt的网络流量监测应用程序，它集成了BandwidthD功能，允许用户实时监控和可视化他们的网络带宽使用情况。对于家庭网络管理，小型办公室或SOHO环境来说，这是一个非常实用的工具。技术分析1.BandwidthD与LuCI集成项目的核心是BandwidthD，这是一款老牌的网络流量检测软件，通过监
  • 新版征信对你有什么影响？ 领跑者_9876
    2019年新版征信，八大变化与你有关！前段时间，网络流传一份带有“培训参考”水印的新版个人征信报告。这份完整版的授信机构版个人征信报告有15页，较之旧版个人征信报告内容丰富不少，涉及数据维度众多。新版征信对于银行来说，能查询到的信息更全面，而对于用户来说，能隐藏的信息越来越少。可以说，新版征信让“老赖”无所遁形！有消息称，央行即将于2019年5月正式上线新版征信报告，目前已经处于试运行阶段。同时，
  • Linux统计进程网络,Linux进程网络流量统计 德云色 Linux统计进程网络
    原标题：Linux进程网络流量统计前言linux都有相应开源工具实时采集网络连接、进程等信息其中网络连接一般包括最基本的五元组信息(源地址、目标地址、源端口、目标端口、协议号)再加上所属进程信息pid,exe,cmdline)等。其中这两项数据大多可直接读取linux/proc目录下的网络状态连接文件/proc/net/tcp、/proc/net/udp),进程状态目录(/proc/pid/xx)
  • linux查看具体进程占用的网络流量 寰宇001 Ubuntu
    监控网络宽带（网速）的18个命令下面是按功能划分的命令名称。监控总体带宽使用――nload、bmon、slurm、bwm-ng、cbm、speedometer和netload监控总体带宽使用（批量式输出）――vnstat、ifstat、dstat和collectl每个套接字连接的带宽使用――iftop、iptraf、tcptrack、pktstat、netwatch和trafshow每个进程的带宽
  • 网络ACL详解-从原理到实战模拟 CloudJourney 网络学习
    引言在复杂多变的网络环境中，保障网络安全和数据传输的合法性、高效性至关重要。访问控制列表（AccessControlLists，简称ACL）作为网络安全的重要组成部分，广泛应用于各种网络设备中，用以控制网络流量的流向和访问权限。本文将以华为网络设备为体系，深入探讨ACL的定义、原理、内部流程、应用场景，并通过实战案例展示其配置和应用方法。一、ACL的定义与原理1.1定义访问控制列表（ACL）是一种
  • 【DevOps】SD-WAN 详解：定义、架构、优势与应用 Coder加油! 运维DevOpsdevops架构运维sdwan
    目录一、传统WAN的局限性二、SD-WAN的解决方案三、SD-WAN的架构四、SD-WAN的关键特点五、SD-WAN的优势六、SD-WAN的应用场景七、总结SD-WAN(Software-DefinedWideAreaNetwork)是一种利用软件定义网络(SDN)技术来简化分支机构与数据中心或云端之间连接的网络架构。它通过集中控制和自动化，优化网络流量路径，提高网络性能和灵活性，并降低运营成本。
  • 基于流谱理论的SSL/TLS协议攻击检测方法 米朵儿技术屋 大数据与数字化的设计应用专栏ssl网络协议网络
    摘要网络攻击检测在网络安全中扮演着重要角色。网络攻击检测的对象主要为僵尸网络、SQL注入等攻击行为。随着安全套接层/安全传输层（SSL/TLS）加密协议的广泛使用，针对SSL/TLS协议本身发起的SSL/TLS攻击日益增多，因此通过搭建网络流采集环境，构建了包含4种SSL/TLS攻击网络流与正常网络流的网络流数据集。针对当前网络攻击流检测的可观测性有限、网络流原始时空域分离性有限等问题，提出流谱理
  • Socks5代理是否支持TCP/UDP协议？ KookeeyLena112 tcp/ipudp网络协议
    Socks5代理是一种网络协议，用于在客户端和服务器之间建立代理连接。它能够通过代理服务器转发网络流量，为用户提供了一种安全、灵活的网络访问方式。关于Socks5代理是否支持TCP/UDP协议，以下是详细解答：一、Socks5代理对TCP协议的支持Socks5代理确实支持TCP协议。这意味着，当客户端需要通过TCP协议进行网络通信时，可以利用Socks5代理来转发TCP流量。这在许多场景中都非常有
  • 令牌桶算法：原理与代码实现 Lill_bin 杂谈网络服务器运维大数据java开发语言后端
    引言令牌桶算法（TokenBucketAlgorithm）是一种网络流量整形（TrafficShaping）和速率限制（RateLimiting）的算法。它能够限制数据传输的平均速率，同时允许某种程度的突发传输。在许多场景中，如网络带宽管理、API速率限制等，令牌桶算法都得到了广泛的应用。原理令牌桶算法的核心思想是使用一个虚拟的“桶”来存储令牌，每个令牌代表一个数据包的传输权限。系统按照固定的速率
  • 后摇，心灵深处的声音 千寻瀑日记
    17年初识后摇，一入耳便觉遇故知。被它清新脱俗的声音所感染。后摇无疑是一股清流，在网络流行歌曲大行其道的时候，她宛如一股清新婉约、厚重深沉的风，吹进人们心中，让灵魂都为之震颤。活着多好，你永远不知道下一秒命运会把什么惊喜送到你面前。当然也有可能是噩耗。不过总也因为这份不确定性，多了几分神秘，让人敬畏。后摇没有多好听，只不过我听了后摇以后再也不想听别的歌。它的旋律，它的唤醒力，听一首后摇，就像走完了
  • 架构设计（13）安全架构设计理论 CoderIsArt 架构设计研究安全架构安全
    网络安全设计网络安全架构设计是为了保护信息系统免受各种网络攻击和威胁而进行的系统化设计。它涉及设计网络基础设施、配置安全控制、制定安全策略，以及实施和维护这些策略，以确保数据的机密性、完整性和可用性。下面是网络安全架构设计的详细内容，包括关键组件、设计原则和实际案例。1.网络安全架构设计的关键组件1.1网络边界保护防火墙：用于过滤网络流量，根据设定的安全规则允许或阻止数据包进入或离开网络。分为传统
  • 如何防范ddos 攻击 ajax_beijing_java ddos
    防护DDoS（分布式拒绝服务）攻击是一个复杂且多方面的任务，需要综合考虑网络架构、硬件设备、软件配置以及安全策略等多个方面。以下是一些主要的防护DDoS攻击的方法：1.流量清洗（TrafficScrubbing）定义：通过实时监测和过滤进入的网络流量，识别并过滤掉DDoS攻击流量，仅将合法流量传送到目标服务器。实施方式：使用专业的DDoS清洗设备或云服务，这些设备和服务在网络边缘或云端建立监控节点
  • linux网络流程分析（一）---网卡驱动 wang603603 linuxlinux
    转载：https://www.cnblogs.com/gogly/archive/2012/06/10/2541573.html分析linux网络的书已经很多了，包括《追踪LinuxTCP/IP代码运行》《Linux内核源码剖析——TCP/IP实现》，这里我只是从数据包在linux内核中的基本流程来分析，尽可能的展现一个主流程框架。内核如何从网卡接收数据,传统的过程：1.数据到达网卡；2.网卡产生
  • 网站被屏蔽的解决方法 白总Server htmljavapython数据结构数据库
    1.检查网络连接：首先确认您的网络连接是否正常。尝试访问其他网站，如果其他网站可以正常打开，那么问题可能是特定网站被屏蔽。2.清除浏览器缓存和Cookie：浏览器的缓存和Cookie可能导致网站无法正常加载。尝试清除浏览器的缓存和Cookie，然后重新访问该网站。3.使用代理服务器或VPN：代理服务器或虚拟私人网络(VPN)可以帮助您绕过网站屏蔽。通过连接到代理服务器或VPN，您可以将您的网络流量
  • 如何解决“来自计算机网络的异常流量” ForRunner123 计算机网络自动化机器学习人工智能ai
    在Google上遇到“您的计算机网络存在异常流量”的错误可能会让人感到沮丧。这个错误信息通常伴随着一个谷歌验证码，您必须解决这个验证码才能继续搜索。这个错误旨在阻止自动化系统对搜索引擎造成过载，但有时会错误地影响正常用户。什么会触发“异常流量”提示？有几个原因可能导致谷歌将您的网络流量标记为异常：谷歌异常流量：验证码快速、重复搜索或来自单个IP地址的大量流量可能会触发验证码，以验证流量是由人类生成
  • Kubernetes中的Kube-proxy：服务发现与负载均衡的基石 liuxin33445566 kubernetes服务发现负载均衡
    摘要Kube-proxy是Kubernetes集群中负责服务发现和负载均衡的关键组件。它通过维护集群内部的网络规则，确保网络流量能够正确地从服务访问点分发到后端的Pod上。本文将详细探讨Kube-proxy的工作原理、配置和使用，以及如何通过编程方式与之交互。1.引言在Kubernetes集群中，服务（Service）是一种抽象，它定义了一种访问容器化应用的方式，无论应用后端的Pod如何变化。Ku
  • SD-WAN降低网络运维难度的关键技术解析 TIANGEKUAJING 网络运维企业组网SD-WAN异地组网
    为什么说SD-WAN（软件定义广域网）大大降低了网络运维的复杂性，主要是因为它的智能路径选择、应用识别和链路质量监测这三个核心技术。这几项在SD-WAN中尤为重要的技术，它们共同作用，提升了整体网络性能，为网络管理提供了更为智能、高效的解决方案。智能路径优化：提升网络性能智能路径优化技术是SD-WAN的重要组成部分，它能够动态分析网络流量和链路状态，从而选择最优路径，实现负载均衡并优化网络性能。无
  • Spring Cloud LoadBalancer 源码解析 码农爱java 【SpringCloudGateway】springcloud微服务负载均衡LoadBalancer源码
    前言LoadBalancer（负载均衡器）：一种网络设备或软件机制，用于分发传入的网络流量负载到多个后端目标服务器上，依次来提高系统的可用性和性能，SpringCloud2020版本以后，移除了对Netflix的依赖，也就移除了负载均衡器Ribbon，SpringCloud官方推荐使用Loadbalancer替换Ribbon，并成为了SpringCloud负载均衡器的唯一实现。LoadBalanc
  • 【算法基础实验】排序-最小索引优先队列IndexMinPQ Greyplayground 算法
    回顾最小优先队列MinPQ理论知识概述在算法和数据结构中，优先队列是一种特殊的队列数据结构，每个元素都有一个优先级。当你从优先队列中删除元素时，通常会删除具有最高（或最低）优先级的元素。在最小优先队列中，优先级最低的元素最先被删除。索引最小优先队列是优先队列的一种变体，允许你通过索引（或键）快速地更新、插入、删除和访问最小元素。它的典型应用包括网络流、图算法（如Dijkstra最短路径算法）等。基
  • python的scapy库基础使用 蜗牛学苑_武汉 网络安全pythonscapyTCP三次握手TCP四次挥手
    scapy库一.概述Scapy是一个功能强大且灵活的Python库，用于操作和探索计算机网络中的数据包。它允许用户构建各种类型的网络数据包，并支持多种网络协议，如TCP、UDP、ICMP、ARP等。Scapy不仅可以发送和接收数据包，还可以捕获、修改和解析网络流量，使用户能够深入研究网络通信并进行网络安全测试。二.scapy的基本使用依赖npcap,最好是最新版本安装:pipinstallscap
  • 关于旗正规则引擎下载页面需要弹窗保存到本地目录的问题 何必如此 jsp超链接文件下载窗口
    生成下载页面是需要选择“录入提交页面”，生成之后默认的下载页面<a>标签超链接为：<a href="<%=root_stimage%>stimage/image.jsp?filename=<%=strfile234%>&attachname=<%=java.net.URLEncoder.encode(file234filesourc
  • 【Spark九十八】Standalone Cluster Mode下的资源调度源代码分析 bit1129 cluster
    在分析源代码之前，首先对Standalone Cluster Mode的资源调度有一个基本的认识： 首先，运行一个Application需要Driver进程和一组Executor进程。在Standalone Cluster Mode下，Driver和Executor都是在Master的监护下给Worker发消息创建(Driver进程和Executor进程都需要分配内存和CPU，这就需要Maste
  • linux上独立安装部署spark daizj linux安装spark1.4部署
    下面讲一下linux上安装spark，以 Standalone Mode 安装   1）首先安装JDK   下载JDK：jdk-7u79-linux-x64.tar.gz  ，版本是1.7以上都行，解压 tar -zxvf jdk-7u79-linux-x64.tar.gz     然后配置 ~/.bashrc&nb
  • Java 字节码之解析一 周凡杨 java字节码javap
        一： Java 字节代码的组织形式   类文件 {     OxCAFEBABE ，小版本号，大版本号，常量池大小，常量池数组，访问控制标记，当前类信息，父类信息，实现的接口个数，实现的接口信息数组，域个数，域信息数组，方法个数，方法信息数组，属性个数，属性信息数组 } &nbs
  • java各种小工具代码 g21121 java
    1.数组转换成List import java.util.Arrays; Arrays.asList(Object[] obj); 2.判断一个String型是否有值 import org.springframework.util.StringUtils; if (StringUtils.hasText(str)) 3.判断一个List是否有值 import org.spring
  • 加快FineReport报表设计的几个心得体会 老A不折腾 finereport
    一、从远程服务器大批量取数进行表样设计时，最好按“列顺序”取一个“空的SQL语句”，这样可提高设计速度。否则每次设计时模板均要从远程读取数据，速度相当慢！！ 二、找一个富文本编辑软件（如NOTEPAD+）编辑SQL语句，这样会很好地检查语法。有时候带参数较多检查语法复杂时，结合FineReport中生成的日志，再找一个第三方数据库访问软件（如PL/SQL）进行数据检索，可以很快定位语法错误。
  • mysql linux启动与停止 墙头上一根草
    如何启动/停止/重启MySQL一、启动方式1、使用 service 启动：service mysqld start2、使用 mysqld 脚本启动：/etc/inint.d/mysqld start3、使用 safe_mysqld 启动：safe_mysqld&二、停止1、使用 service 启动：service mysqld stop2、使用 mysqld 脚本启动：/etc/inin
  • Spring中事务管理浅谈 aijuans spring事务管理
    Spring中事务管理浅谈 By Tony Jiang@2012-1-20 Spring中对事务的声明式管理 拿一个XML举例 [html]  view plain copy print ? <?xml version="1.0" encoding="UTF-8"?>&nb
  • php中隐形字符65279（utf-8的BOM头）问题 alxw4616
    php中隐形字符65279（utf-8的BOM头）问题 今天遇到一个问题. php输出JSON 前端在解析时发生问题:parsererror.   调试: 1.仔细对比字符串发现字符串拼写正确.怀疑是 非打印字符的问题. 2.逐一将字符串还原为unicode编码. 发现在字符串头的位置出现了一个 65279的非打印字符.        
  • 调用对象是否需要传递对象(初学者一定要注意这个问题) 百合不是茶 对象的传递与调用技巧
        类和对象的简单的复习,在做项目的过程中有时候不知道怎样来调用类创建的对象,简单的几个类可以看清楚,一般在项目中创建十几个类往往就不知道怎么来看   为了以后能够看清楚,现在来回顾一下类和对象的创建,对象的调用和传递(前面写过一篇)   类和对象的基础概念:   JAVA中万事万物都是类 类有字段(属性),方法,嵌套类和嵌套接
  • JDK1.5 AtomicLong实例 bijian1013 javathreadjava多线程AtomicLong
    JDK1.5 AtomicLong实例 类 AtomicLong 可以用原子方式更新的 long 值。有关原子变量属性的描述，请参阅 java.util.concurrent.atomic 包规范。AtomicLong 可用在应用程序中（如以原子方式增加的序列号），并且不能用于替换 Long。但是，此类确实扩展了 Number，允许那些处理基于数字类的工具和实用工具进行统一访问。  
  • 自定义的RPC的Java实现 bijian1013 javarpc
            网上看到纯java实现的RPC，很不错。         RPC的全名Remote Process Call，即远程过程调用。使用RPC，可以像使用本地的程序一样使用远程服务器上的程序。下面是一个简单的RPC 调用实例，从中可以看到RPC如何
  • 【RPC框架Hessian一】Hessian RPC Hello World bit1129 Hello world
    什么是Hessian The Hessian binary web service protocol makes web services usable without requiring a large framework, and without learning yet another alphabet soup of protocols. Because it is a binary p
  • 【Spark九十五】Spark Shell操作Spark SQL bit1129 shell
    在Spark Shell上，通过创建HiveContext可以直接进行Hive操作   1. 操作Hive中已存在的表   [hadoop@hadoop bin]$ ./spark-shell Spark assembly has been built with Hive, including Datanucleus jars on classpath Welcom
  • F5　往header加入客户端的ip ronin47
    when HTTP_RESPONSE {if {[HTTP::is_redirect]}{         HTTP::header replace Location [string map {:port/ /} [HTTP::header value Location]]HTTP::header replace Lo
  • java-61-在数组中，数字减去它右边(注意是右边)的数字得到一个数对之差. 求所有数对之差的最大值。例如在数组{2, 4, 1, 16, 7, 5, bylijinnan java
    思路来自： http://zhedahht.blog.163.com/blog/static/2541117420116135376632/ 写了个java版的 public class GreatestLeftRightDiff { /** * Q61.在数组中，数字减去它右边(注意是右边)的数字得到一个数对之差。 * 求所有数对之差的最大值。例如在数组
  • mongoDB 索引 开窍的石头 mongoDB索引
    在这一节中我们讲讲在mongo中如何创建索引       得到当前查询的索引信息      db.user.find(_id:12).explain();        cursor: basicCoursor 指的是没有索引  &
  • [硬件和系统]迎峰度夏 comsci 系统
      从这几天的气温来看，今年夏天的高温天气可能会维持在一个比较长的时间内    所以，从现在开始准备渡过炎热的夏天。。。。    每间房屋要有一个落地电风扇，一个空调(空调的功率和房间的面积有密切的关系)    坐的，躺的地方要有凉垫，床上要有凉席       电脑的机箱
  • 基于ThinkPHP开发的公司官网 cuiyadll 行业系统
    后端基于ThinkPHP，前端基于jQuery和BootstrapCo.MZ 企业系统 轻量级企业网站管理系统 运行环境:PHP5.3+, MySQL5.0 系统预览 系统下载：http://www.tecmz.com 预览地址：http://co.tecmz.com 各种设备自适应 响应式的网站设计能够对用户产生友好度，并且对于
  • Transaction and redelivery in JMS (JMS的事务和失败消息重发机制) darrenzhu jms事务承认MQacknowledge
    JMS Message Delivery Reliability and Acknowledgement Patterns http://wso2.com/library/articles/2013/01/jms-message-delivery-reliability-acknowledgement-patterns/ Transaction and redelivery in
  • Centos添加硬盘完全教程 dcj3sjt126com linuxcentoshardware
    Linux的硬盘识别: sda        表示第1块SCSI硬盘 hda       表示第1块IDE硬盘 scd0      表示第1个USB光驱 一般使用“fdisk -l”命
  • yii2 restful web服务路由 dcj3sjt126com PHPyii2
    路由 随着资源和控制器类准备，您可以使用URL如 http://localhost/index.php?r=user/create访问资源，类似于你可以用正常的Web应用程序做法。 在实践中，你通常要用美观的URL并采取有优势的HTTP动词。 例如，请求POST /users意味着访问user/create动作。 这可以很容易地通过配置urlManager应用程序组件来完成 如下所示
  • MongoDB查询(4)——游标和分页[八] eksliang mongodbMongoDB游标MongoDB深分页
    转载请出自出处：http://eksliang.iteye.com/blog/2177567 一、游标         数据库使用游标返回find的执行结果。客户端对游标的实现通常能够对最终结果进行有效控制，从shell中定义一个游标非常简单，就是将查询结果分配给一个变量（用var声明的变量就是局部变量），便创建了一个游标，如下所示： > var
  • Activity的四种启动模式和onNewIntent() gundumw100 android
    Android中Activity启动模式详解 　　在Android中每个界面都是一个Activity，切换界面操作其实是多个不同Activity之间的实例化操作。在Android中Activity的启动模式决定了Activity的启动运行方式。 　　Android总Activity的启动模式分为四种： Activity启动模式设置： <acti
  • 攻城狮送女友的CSS3生日蛋糕 ini htmlWebhtml5csscss3
    在线预览：http://keleyi.com/keleyi/phtml/html5/29.htm   代码如下：   <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title>攻城狮送女友的CSS3生日蛋糕-柯乐义<
  • 读源码学Servlet（1）GenericServlet 源码分析 jzinfo tomcatWebservlet网络应用网络协议
    Servlet API的核心就是javax.servlet.Servlet接口，所有的Servlet 类（抽象的或者自己写的）都必须实现这个接口。在Servlet接口中定义了5个方法，其中有3个方法是由Servlet 容器在Servlet的生命周期的不同阶段来调用的特定方法。     先看javax.servlet.servlet接口源码：  package
  • JAVA进阶：VO(DTO)与PO(DAO)之间的转换 snoopy7713 javaVOHibernatepo
      PO即 Persistence Object　　VO即 Value Object 　VO和PO的主要区别在于：　　VO是独立的Java Object。　　PO是由Hibernate纳入其实体容器（Entity Map）的对象，它代表了与数据库中某条记录对应的Hibernate实体，PO的变化在事务提交时将反应到实际数据库中。 　实际上，这个VO被用作Data Transfer
  • mongodb group by date 聚合查询日期 统计每天数据（信息量） qiaolevip 每天进步一点点学习永无止境mongodb纵观千象
    /* 1 */ { "_id" : ObjectId("557ac1e2153c43c320393d9d"), "msgType" : "text", "sendTime" : ISODate("2015-06-12T11:26:26.000Z")
  • java之18天 常用的类(一) Luob. MathDateSystemRuntimeRundom
    System类 import java.util.Properties; /** * System: * out:标准输出,默认是控制台 * in:标准输入,默认是键盘 * * 描述系统的一些信息 * 获取系统的属性信息:Properties getProperties(); * * * */ public class Sy
  • maven wuai maven
    1、安装maven：解压缩、添加M2_HOME、添加环境变量path 2、创建maven_home文件夹，创建项目mvn_ch01,在其下面建立src、pom.xml，在src下面简历main、test、main下面建立java文件夹 3、编写类，在java文件夹下面依照类的包逐层创建文件夹，将此类放入最后一级文件夹 4、进入mvn_ch01 4.1、mvn compile ,执行后会在
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他