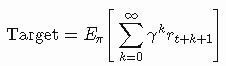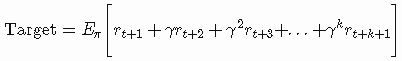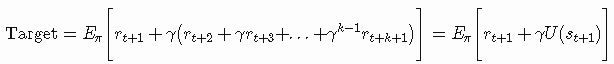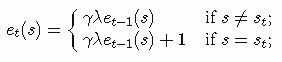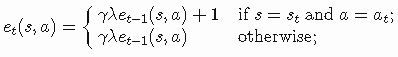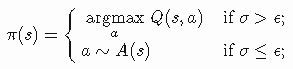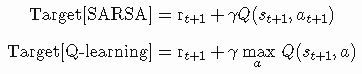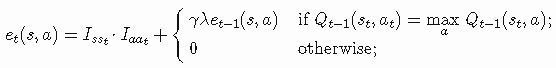剖析强化学习 - 第三部分

作者：Massimiliano Patacchiola

欢迎来到“剖析强化学习”系列的第三部分。在第一篇和第二篇文章中，我们分析了动态规划和蒙特卡罗（MC）方法。第三部分要讲的强化学习技术称为时间差分（TD）方法。TD学习解决了MC学习中出现的一些问题，在第二部分的结论中我描述了这个问题之一，使用MC方法，需要等到episode结束才更新效用函数，这是一个严重的问题，因为一些应用程序可能会有很长的episode，因此延迟到终点的学习导致速度太慢；此外，episode的终止并不总是得到保证。我们将看到TD方法如何解决这些问题。

在这篇文章中，我将从TD方法的一般介绍开始，然后讲解最著名（最常用）的TD技术，即Sarsa和Q-Learning。TD对强化学习产生了巨大影响，并且大多数最新出版物（包括深度强化学习）均基于TD方法。我们将通过动物学习实验来了解TD与心理学的关系。如果你想了解更多有关TD和动物学习的知识，你应该阅读Sutton和Barto的书（pdf）的第二版第14章和该作者题为“巴甫洛夫强化的时间导数模型”的另一篇文章，您可以在Google上轻松找到它。这篇文章的某些部分是基于经典的“强化学习：介绍”的第6章和第7章。如果读完这篇文章后你不满意，建议你看一下Sutton的文章“学习用时间差分的方法来预测”。如果你想了解更多关于Sarsa和Q-learning的知识，你可以阅读Russel和Norvig的书（21.3.2章）。Mitchell在他的书Machine Learning（1997）（第13章）中也提供了强化学习和Q-Learning的简短介绍。这篇文章的最后一部分提供了这些资源的链接。

时间差分（兔子）

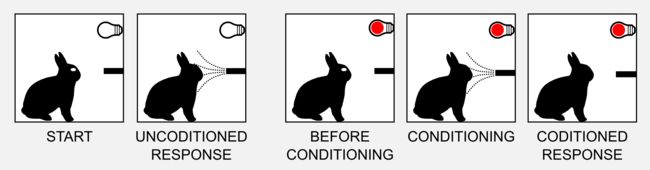
时间差分(Temporal Differencing)一词在1988年被Sutton首次使用。Sutton是一位自由主义者，心理学家和计算机科学家，对了解我们的智力和目标导向行为的含义有浓厚的兴趣。如果您想了解更多信息，请查看他的个人网站。Sutton研究的有趣之处在于他从动物学习理论的角度出发并解释了TD，并表明TD模型通过简单的时间导数方法解决了许多问题。你们中许多人都听说过著名的巴甫洛夫在经典条件反射的实验中，向狗展示食物引起反应（流涎），这种关联被称为无条件反射（UR），它是由无条件刺激（US）引起的。UR是一种自然的反应，不依赖于以前的经验。在第二阶段，我们将刺激（食物）与中性刺激（例如钟声）配对，一段时间后，狗会将钟的声音与食物联系起来，这种关联会引起流涎。钟被称为条件刺激（CS），引起的反应是条件反射（CR）。

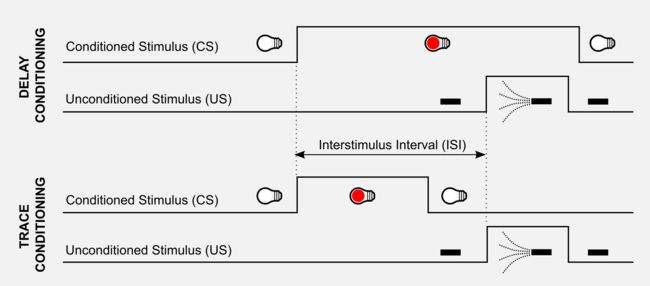
在兔子的眨眼条件反射中研究得出同样的结论。轻轻的一股空气直接射向兔子的眼睛，在这种情况下，UR是关闭眼睑，而US是吹气，在条件反射过程中，在吹气之前打开红灯（CS），条件反射会在光线和眨眼之间产生关联。经典条件反射实验中有两种类型的刺激安排。在延迟反射(delay conditioning)中，CS在整个US过程中无任何间隔地延伸。在痕迹反射(trace conditioning)中，在CS和US之间存在称为痕迹间隔的时间间隔。CS和US之间的延迟是一个重要的变量，称为刺激间隔（ISI）。

了解刺激之间的预测关系对于存活非常重要，这就是为什么它广泛存在于从小鼠到人类的各种物种中的原因。学习意味着在每个时间点准确预测未来US强度水平的迫切性加权总和(imminence-weightedsum)。在眨眼实验中观察到兔子对US之前发出的CS的预测较弱。研究眨眼条件反射的结果，Sutton和Barto（1990）发现了与TD框架的相关性。强化是根据其迫切性（ISI的长度）加权的，稍稍延迟时，它的权重稍微减轻，长时间延迟时它的权重很小，等等。这个假设是的经典条件反射TD模型的核心，它是Rescorla-Wagner模型（1972）的延伸。如果你阅读以前的文章，你应该发现和折扣奖励概念的一些相似之处。TD背后的一般规则适用于兔子和人工Agent,这个一般规则可以概括如下：

NewEstimate←OldEstimate+StepSize[Target−OldEstimate]

表达式[Target−OldEstimate]是估计误差或δ，它可以减少并朝向实际价值（Target）移动。StepSize（有时称为学习率）是一个参数，它决定了误差在何种程度上被纳入到新估计,当StepSize=0时Agent根本不学习，当StepSize=1时Agent只考虑最新的信息，在某些应用中，StepSize会在每个时间步骤改变。处理第k个奖励参数更新为1/k 。然而在实践中，对于所有步骤而言，经常使用诸如0.1的恒定值。在我们的案例中什么是Target？从第二篇文章中，我们知道我们可以估计一个状态的实际效用，作为该状态回报的预期，Target是状态的预期回报：

在估计目标的MC方法中，我们考虑了所有访问的状态直到episode结束：

在TD算法中，我们希望在每次访问后更新效用函数，因为这个原因，我们没有所有的状态，也没有奖励的值，唯一可用的信息是t+1时刻的奖励rt + 1和之前估计的效用。我们要找到一种只用这些值来表达目标的方法，为了解决这个问题，我们可以使用自助(bootstrap )，这意味着我们可以使用估计来建立新的估计。以下最重要的部分，如果我们将γ分组，我们就恰好得到了U(st+1) 公式：

这样我们得到了我们想要的。现在Target由两个量表示：rt + 1和U(st+1) ，并且他们都是已知的。包含所有这些考虑因素，我们最终可以写出完整的更新规则：

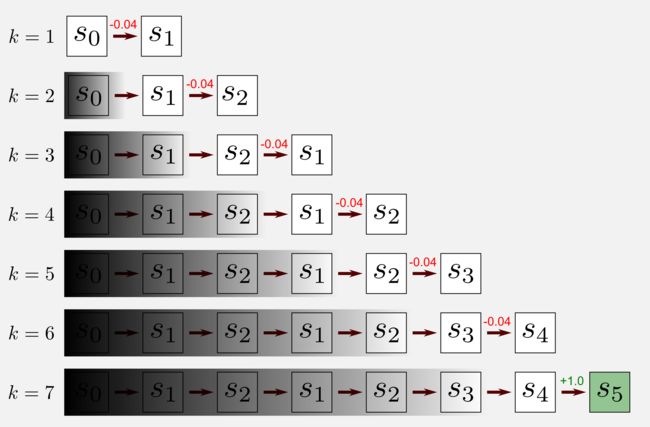
此更新规则非常吸引人。在第一次迭代中，我们使用随机值（或零）初始化效用值，接着我们要做的是取t+1时刻的其中一个值更新t时刻的状态。算法如何收敛到实际值？当Agent第一次遇到终止状态时，神奇就会发生，在这种特殊情况下，TD和MC获得的回报是一致的。再次使用我们的清洁机器人，我们可以轻松了解TD和MC学习之间的区别以及每一步做的每一件事...

TD(0)Python实现

前一部分中的更新规则是TD学习的最简单形式，即TD(0)算法，TD(0)允许根据特定策略估算效用值。我们处于预测的被动学习案例，而且我们处于无模型强化学习阶段，这意味着我们没有转移模型。为了估计效用函数，我们只能在世界中移动。再次使用清洁机器人示例，我想向您展示将TD算法应用于单个episode，我将使用第二个帖子的episode，其中机器人以（1,1）开始并且在七步之后到达（4,3）的终止状态。

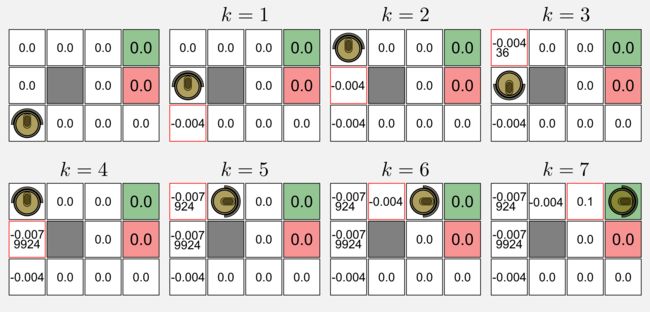
应用TD算法意味着仅考虑t处的状态和t + 1处的状态来逐步移动，就是在每一步之后，我们得到t + 1的效用值和回报，并更新t的值。TD(0)算法忽略过去的状态，这可以由我在上面添加阴影的那些状态表示出。将该算法应用于episode（γ = 0.9，α = 0.1）会导致效用矩阵发生以下更改：

高亮红色边框显示了效用值已经在每次访问更新，矩阵初始化为零。在k = 1时，状态（1,1）被更新是由于机器人处于状态（1,2）并获得第一个奖励（-0.04），（1,1）更新效用的计算如下：0.0 + 0.1 (-0.04 + 0.9 (0.0) - 0.0) = -0.004；与（1,1）类似，该算法同样方式更新（1,2）处的状态；在k = 3时，机器人返回并且计算形式如下：0.0 + 0.1(-0.04 + 0.9 (-0.004) - 0.0) = -0.00436；在k = 4时，机器人再次改变方向，在这种情况下，算法第二次更新状态（1,2）如下：-0.004 + 0.1 (-0.04 + 0.9 (-0.00436) + 0.004)= -0.0079924。应用相同的过程直到episode结束。

在Python实现中，像我们在第二篇文章中所做的那样，我们使用模块gridworld.py中包含的类GridWorld来创建网格世界。我将再次使用4x3世界，其中（4,3）是充电站，（4,2）是楼梯，在这个世界中将获得与以前的帖子中获得的相同的最优策略和效用值。

Optimal policy:			Utility Matrix:

 >   >   >   * 			0.812  0.868  0.918  1.0
 ^   #   ^   * 			0.762  0.0    0.660 -1.0
 ^   <   <   <. 		0.705  0.655  0.611  0.388

TD(0)的更新规则可以实现为下面的几行代码。

 

def update_utility(utility_matrix, observation, new_observation, 
                   reward, alpha, gamma):
    '''Return the updated utility matrix

    @param utility_matrix the matrix before the update
    @param observation the state observed at t
    @param new_observation the state observed at t+1
    @param reward the reward observed after the action
    @param alpha the step size (learning rate)
    @param gamma the discount factor
    @return the updated utility matrix
    '''
    u = utility_matrix[observation[0], observation[1]]
    u_t1 = utility_matrix[new_observation[0], new_observation[1]]
    utility_matrix[observation[0], observation[1]] += \
        alpha * (reward + gamma * u_t1 - u)
    return utility_matrix

主循环比MC方法中实现得简单得多。在这种情况下，我们没有任何首次访问约束，唯一要做的就是应用更新规则。

 

for epoch in range(tot_epoch):
    #Reset and return the first observation
    observation = env.reset(exploring_starts=True)
    for step in range(1000):
        #Take the action from the action matrix
        action = policy_matrix[observation[0], observation[1]]
        #Move one step in the environment and get obs and reward
        new_observation, reward, done = env.step(action)
        #Update the utility matrix using the TD(0) rule
        utility_matrix = update_utility(utility_matrix, 
                                        observation, new_observation, 
                                        reward, alpha, gamma)
        observation = new_observation
        if done: break #return

文件temporal_differencing_prediction.py提供了完整的代码，可在GitHub存储库中找到。获得算法背后的核心思路非常重要，使用gamma=0.999，alpha=0.1运行完整的代码，遵循最优策略我们获得了-0.04的奖励：

 

Utility matrix after 1 iterations:
[[-0.004  -0.0076  0.1     0.    ]
 [ 0.      0.      0.      0.    ]
 [ 0.      0.      0.      0.    ]]

Utility matrix after 2 iterations:
[[-0.00835924 -0.00085     0.186391    0.        ]
 [-0.0043996   0.          0.          0.        ]
 [-0.004       0.          0.          0.        ]]

Utility matrix after 3 iterations:
[[-0.01520748  0.01385546  0.2677519   0.        ]
 [-0.00879473  0.          0.          0.        ]
 [-0.01163916 -0.0043996  -0.004      -0.004     ]]

...

Utility matrix after 100000 iterations:
[[ 0.83573452  0.93700432  0.94746457  0.        ]
 [ 0.77458346  0.          0.55444341  0.        ]
 [ 0.73526333  0.6791969   0.62499965  0.49556852]]

...

Utility matrix after 300000 iterations:
[[ 0.85999294  0.92663558  0.99565229  0.        ]
 [ 0.79879005  0.          0.69799246  0.        ]
 [ 0.75248148  0.69574141  0.65182993  0.34041743]]

现在我们可以对TD(0)获得的效用矩阵和第一篇文章中使用动态规划获得的效用矩阵进行比较：

大部分值是相似的，两个表格的主要区别在于对两个终止状态的估计。TD(0)不适用于终止状态，因为我们需要获得下一个t + 1时状态的奖励和效用，根据定义终止状态后不存在另一个状态。然而，这不是一个大问题，我们想知道是终止状态附近各状态的效用。为了克服这个问题，经常使用一个简单的条件判断来处理终止状态：

 

if (is_terminal(state) == True):
    utility_matrix(state) = reward

很棒，我们看到了TD(0)是如何工作的，但是我没有谈论关于：算法名称中包含的0是什么意思？要理解0这意味着我必须介绍资格痕迹(eligibility traces)。

TD(λ)和资格痕迹

正如我在前一节中告诉你的，TD(0)算法没有考虑过去的状态,TD(0)中重要的是当前状态和t + 1时的状态。然而，将在t + 1学到的知识也延伸到以前的状态会有用处，可以加速学习。为了实现这个目标，有必要建立一个短期记忆机制来存储在最后步骤中访问过的状态。对于每个在时间t的状态s我们可以定义et(s)作为资格痕迹(eligibility trace)：

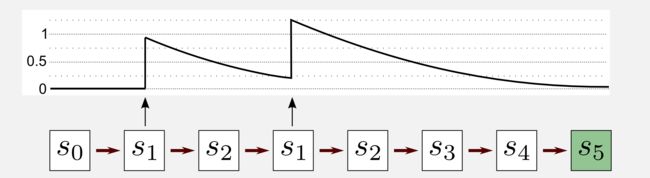
这里γ是折扣率，λ∈[0,1]是一个衰减参数，称为痕迹衰减(trace-decay)或累积痕迹，它定义每个访问状态的更新权重。当0<λ<1时痕迹随时间减少，这允许给不频繁的状态一个小的权重；当λ=0时即TD(0) 的情况，只有前面的预测被更新；当λ=1时即TD(1)其中所有前面的预测都被相同地更新。TD(1)可以被认为是使用TD框架的MC方法的扩展。在MC方法中，我们需要等待episode结束才能更新状态，在TD(1)中，我们可以在线更新所有之前的状态，我们不需要等该episode的结束。现在让我们来看看在一个episode中特定状态痕迹会发生什么。考虑一个episode七次访问中有五个状态被访问，状态s1在episode中访问两次，让我们看看它的痕迹。

开始时痕迹等于零。在首次访问s1（第二步）后，曲线上升到1，然后开始衰减。第二次访问（第四步）后，将+1添加到当前值（0.25），获得1.25的最终痕迹。该点之后，状态s1不再被访问，并且痕迹缓慢地变为零。TD(λ)如何更新效用函数？ 在TD(0)中，我们看到在图形中添加了统一的阴影来表示以前状态的不可访问性。在TD(λ)中，以前的状态是可访问的，但它们是根据资格痕迹值进行更新的。具有较小资格痕迹的状态将会少量更新，而具有较高资格痕迹的状态将会显著性更新。

在上图中，我们可以用不均匀的阴影表示TD(λ)，阴影部分隐藏了旧的状态并完全显示了最近的状态。现在是为TD(λ)定义更新规则的时候了，记住估计误差δ 在上一节中定义为：

我们可以如下所示更新效用函数：

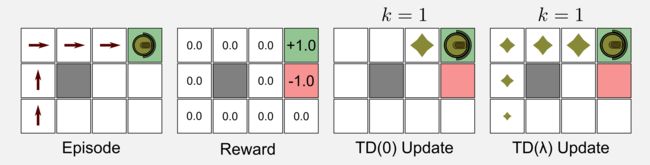
为了更好地理解TD(0)和TD(λ)之间的差异，我构建了一个4x3的网格世界，其中对于除两个终止状态之外的所有状态的奖励为零，该效用矩阵被初始化为零。我考虑的episode包含五次访问，机器人从状态（1,1）开始，并按照最佳路径到达充电站（4,3）。

TD(0)和TD(λ)更新的结果在所有访问中除了最后一次访问都是相同的（零）。当机器人到达充电站（奖励+1.0）时，更新规则返回正值。在TD(0)中，结果只传播到前一个状态（3,3）；在TD(λ)中，由于资格痕迹，结果会传播回所有之前的状态，痕迹的衰减值给予最后状态更多的权重。正如我告诉你的，效用痕迹踪机制有助于加速收敛。很容易理解，为什么在我们的例子中TD(0)需要5个episode才能达到TD(λ)相同的结果。

TD(λ)的Python实现很简单，我们只需要添加一个资格(eligibility)矩阵及其更新规则。

 

def update_utility(utility_matrix, trace_matrix, alpha, delta):
    '''Return the updated utility matrix

    @param utility_matrix the matrix before the update
    @param alpha the step size (learning rate)
    @param delta the error (Taget-OldEstimte) 
    @return the updated utility matrix
    '''
    utility_matrix += alpha * delta * trace_matrix
    return utility_matrix

def update_eligibility(trace_matrix, gamma, lambda_):
    '''Return the updated trace_matrix

    @param trace_matrix the eligibility traces matrix
    @param gamma discount factor
    @param lambda_ the decaying value
    @return the updated trace_matrix
    '''
    trace_matrix = trace_matrix * gamma * lambda_
    return trace_matrix

与TD(0)情况相比，主循环引入了一些新组件。我们在一个单独的行中有delta估计，另外两行有对trace_matrix的管理。所有状态首先增加（+1）然后他们被衰减。

 

for epoch in range(tot_epoch):
  #Reset and return the first observation
  observation = env.reset(exploring_starts=True)
  for step in range(1000):
    #Take the action from the action matrix
    action = policy_matrix[observation[0], observation[1]]
    #Move one step in the environment and get obs and reward
    new_observation, reward, done = env.step(action)
    #Estimate the error delta (Target - OldEstimate)
    delta = reward + gamma * \
        utility_matrix[new_observation[0], new_observation[1]] - \
        utility_matrix[observation[0], observation[1]]
    #Adding +1 in the trace matrix (only the state visited)
    trace_matrix[observation[0], observation[1]] += 1
    #Update the utility matrix (all the states)
    utility_matrix = update_utility(utility_matrix, trace_matrix, alpha, delta)
    #Update the trace matrix (decaying) (all the states)
    trace_matrix = update_eligibility(trace_matrix, gamma, lambda_)
    observation = new_observation
    if done: break #return

temporal_differencing_prediction_trace.py文件中有完整的代码，在GitHub存储库上可以找到。运行脚本我们获得下列效用矩阵：

 

Utility matrix after 1 iterations:
[[ 0.       0.04595  0.1      0.     ]
 [ 0.       0.       0.       0.     ]
 [ 0.       0.       0.       0.     ]]

...

Utility matrix after 101 iterations:
[[ 0.90680695  0.98373981  1.05569002  0.        ]
 [ 0.8483302   0.          0.6750451   0.        ]
 [ 0.77096419  0.66967837  0.50653039  0.22760573]]

...

Utility matrix after 100001 iterations:
[[ 0.86030512  0.91323552  0.96350672  0.        ]
 [ 0.80914277  0.          0.82155788  0.        ]
 [ 0.76195244  0.71064599  0.68342933  0.48991829]]

...

Utility matrix after 300000 iterations:
[[ 0.87075806  0.92693723  0.97192601  0.        ]
 [ 0.82203398  0.          0.87812674  0.        ]
 [ 0.76923169  0.71845851  0.7037472   0.52270127]]

将最终效用矩阵与TD(0)中不使用资格痕迹而获得的效用矩阵进行比较，您会注意二者具有相似的值。有人可能会问：使用资格痕迹的优势是什么？资格痕迹版本收敛更快速。在大型状态空间中处理稀疏奖励时，这一优势变得更加明显。在这种情况下，资格痕迹机制可以在t+1学习到的内容传播回最后访问的状态以显著加快收敛。

SARSA：时间差分控制

现在是将TD方法扩展到控制实例的时候了，在这里我们的例子是积极的(active)场景，从随机数开始估计最优策略。我们在之前的介绍中看到，TD(0)案例的最终更新规则是：

更新规则基于元组State-Reward-State，请记住，现在我们处于控制场景。在这里，我们使用Q函数（请参阅第二篇文章）来估计最佳策略，Q函数需要输入一个状态-动作对。用于控制的TD算法非常简单，看看更新规则将立即使您了解它的工作原理：

就是这样，在更新规则中我们简单地用Q取代了U。我们必须小心，因为二者有区别，现在我们需要一个新的值，即在t+ 1时的动作。这不是问题，因为它包含在Q-矩阵中。在TD控制中，估计基于元组State-Action-Reward-State-Action，同时该元组给出了算法的名称：SARSA。1994年，Rummery和Niranjan在“使用连接系统的在线Q-Learning”一文中介绍了SARSA ，最初被称为修改的Q-learning。1996年Sutton使用了当前的名字。

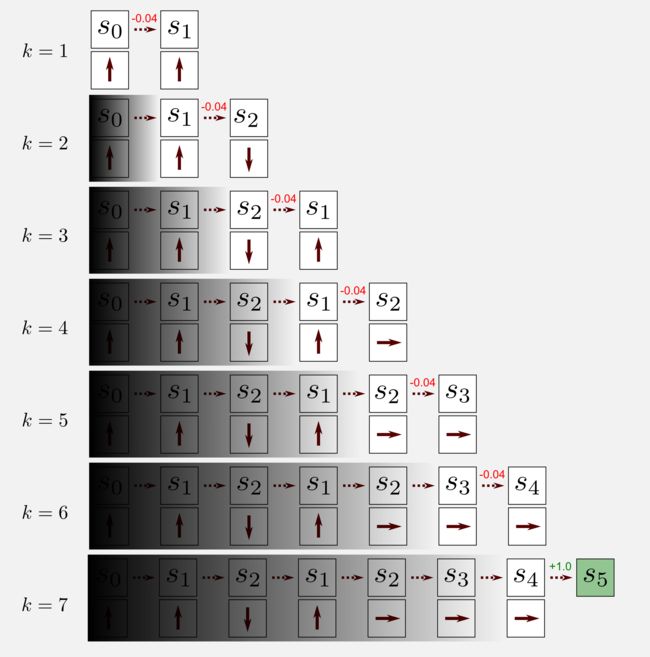
为了获得算法背后的动机，我们再次考虑Agent在世界中移动一个episode的情形。机器人从s0开始经过七次访问后到达终点状态s5，对于每个状态，我们都有相关的动作。依照算法移动仅考虑t和t + 1时的状态，在SARSA的标准实现中，先前的状态被忽略，如图中的阴影所示，这与TD(0)部分解释的TD框架一致。现在我想总结一下算法的所有步骤：

1.移动一步并从π(st)中选择at

2.观察：rt+1, st+1, at+1

3.更新状态-动作函数Q(st,at)

4.更新策略：

在步骤1中，Agent从策略中选择一个动作并向前移动一步;在步骤2中，Agent观察奖励、新状态和相关动作；在步骤3中，算法使用更新规则更新状态-动作函数；在步骤4中，我们使用与控制MC相同的机制（参见第二篇文章），在每次访问时选择具有最高状态-动作值的动作更新策略π，这促使策略贪婪(greedy)，这里总是应用在MC方法中使用的探索开始条件。

我们能否将TD(λ)想法应用于SARSA？答案是可以的。SARSA(λ)遵循TD(λ)的相同步骤执行资格痕迹以加速收敛。该算法背后的意图是相同的，然而不是将预测方法应用于状态SARSA(λ)而是将其应用于状态-动作对。每个状态-动作都有一个痕迹(trace)，并且此痕迹更新如下：

我们使用下面的更新规则更新Q函数：

考虑到在这篇文章中，我介绍了许多新概念，我不会继续使用Python实现SARSA(λ)，考虑把它作为一个家庭作业，你们尝试自己实现它。如果觉得在前面几节中的解释不够，你可以阅读Sutton and Barto的书的第7.5章。

SARSA：Python和ε-greedy策略

SARSA的Python实现需要一个Numpy矩阵state_action_matrix，它可以用随机值初始化或用零填充。在这里你必须记住，我们定义state_action_matrix中每个列是一个状态，每行是一个动作（见第二篇文章）。例如，在4x3网格世界中，通过查询state_action_matrix[0,2]我们得到状态（3,1）（左上角）和动作DOWN的状态-动作值。通过查询state_action_matrix[11, 0]我们得到状态（4,1）（右下角）和动作UP的状态-动作值。像往常一样，我们用Russel和Norvig的惯例来命名状态，左下角是状态（1,1），而在Python中，我们使用Numpy约定[0, 0]定义网格世界的左上角值。SARSA基于以下更新规则来更新状态-动作矩阵：

 

def update_state_action(state_action_matrix, observation, new_observation, 
                   action, new_action, reward, alpha, gamma):
    '''Return the updated utility matrix

    @param state_action_matrix the matrix before the update
    @param observation the state observed at t
    @param new_observation the state observed at t+1
    @param action the action at t
    @param new_action the action at t+1
    @param reward the reward observed after the action
    @param alpha the step size (learning rate)
    @param gamma the discount factor
    @return the updated state action matrix
    '''
    #Getting the values of Q at t and at t+1
    col = observation[1] + (observation[0]*4)
    q = state_action_matrix[action ,col]
    col_t1 = new_observation[1] + (new_observation[0]*4)
    q_t1 = state_action_matrix[new_action ,col_t1]
    #Applying the update rule
    state_action_matrix[action ,col] += \
        alpha * (reward + gamma * q_t1 - q)
    return state_action_matrix

此外，由于这是一个控制的例子，并且我们想估计策略，因此我们还需要更新功能来完成此任务：

 

def update_policy(policy_matrix, state_action_matrix, observation):
    '''Return the updated policy matrix

    @param policy_matrix the matrix before the update
    @param state_action_matrix the state-action matrix
    @param observation the state obsrved at t
    @return the updated state action matrix
    '''
    col = observation[1] + (observation[0]*4)
    #Getting the index of the action with the highest utility
    best_action = np.argmax(state_action_matrix[:, col])
    #Updating the policy
    policy_matrix[observation[0], observation[1]] = best_action
    return policy_matri

该update_policy函数根据算法的步骤4使策略贪婪地选择具有最高值的动作。最后在主循环中episode中的每次访问更新state_action_matrix和policy_matrix。

 

for epoch in range(tot_epoch):
  #Reset and return the first observation
  observation = env.reset(exploring_starts=True)
  for step in range(1000):
    #Take the action from the action matrix
    action = policy_matrix[observation[0], observation[1]]
    #Move one step in the environment and get obs,reward and new action
    new_observation, reward, done = env.step(action)
    new_action = policy_matrix[new_observation[0], new_observation[1]]
    #Updating the state-action matrix
    state_action_matrix = update_state_action(state_action_matrix, 
                                              observation, new_observation, 
                                              action, new_action, 
                                              reward, alpha, gamma)
    #Updating the policy
    policy_matrix = update_policy(policy_matrix, 
                                  state_action_matrix, 
                                  observation)
    observation = new_observation
    if done: break

完整的Python脚本实现在GitHub存储库中的temporal_differencing_control_sarsa.py。使用alpha=0.001和gamma=0.999运行脚本在180000次迭代后产生最优策略。

 

Policy matrix after 1 iterations:
 <   v   >   *  
 ^   #   v   *  
 >   v   v   > 

...

Policy matrix after 90001 iterations:
 >   >   >   *  
 ^   #   ^   *  
 ^   <   ^   < 

...

Policy matrix after 180001 iterations:
 >   >   >   *  
 ^   #   ^   *  
 ^   <   <   < 

SARSA是否总是趋于最优策略？答案是肯定的，只要所有状态-动作对都被无数次访问，SARSA就会以概率1收敛。Russel和Norvig 称此假设为在无限探索极限中的贪婪（GLIE）。GLIE方案必须在每个状态中无限次数尝试每个动作，以避免由于一系列不寻常的结果而错过最佳动作的有限概率。在我们的网格世界里，可能会发生不幸的初始化导致一个糟糕的策略，使Agent远离某些状态。在第二篇文章中，我们使用了探索开始的假设保证对所有状态-动作对的一致性探索。然而，探索开始可能难以应用在一个大的状态空间中。另一种解决方案称为ε-greedy策略。ε-greedy策略探索所有状态，这些状态随机选择最高价值但具有小概率ε的动作。定义0 ≤ σ ≤ 1作为在每个时间步骤采用的统一随机数，A表示一个包含所有可用动作的集合，我们选择一个如下的动作a：

在Python中，我们可以轻松实现这一函数，该函数返回遵循ε-greedy方案的动作：

 

def return_epsilon_greedy_action(policy_matrix, observation, epsilon=0.1):
    tot_actions = int(np.nanmax(policy_matrix) + 1)
    #Getting the greedy action
    action = int(policy_matrix[observation[0], observation[1]])
    #Probabilities of non-greedy actions
    non_greedy_prob = epsilon / tot_actions
    #Probability of the greedy action
    greedy_prob = 1 - epsilon + non_greedy_prob
    #Array containing a weight for each action
    weight_array = np.full((tot_actions), non_greedy_prob)
    weight_array[action] = greedy_prob
    #Sampling the action based on the weights
    return np.random.choice(tot_actions, 1, p=weight_array)

在ε-greedy策略的朴素实现中每个非贪婪动作被赋予相同的概率。实际上有些动作可能比其他动作表现更好。使用softmax分布（例如玻尔兹曼分布）可以给出贪婪动作的最高概率，但不要以相同的方式处理所有其他动作。这里为了简单起见，我将使用朴素的方法实现。探索开始和ε-greedy策略不排斥彼此，它们可以共存，同时使用这两种方法可以带来更快的收敛。让我们尝试使用ε-greedy动作选择来扩展前面的脚本，以查看发生了什么。在主循环中，我们必须用ε-greedy动作替换动作选择。使用gamma=0.999、alpha=0.001和epsilon=0.1运行脚本导致130000次迭代时得到最优策略，意味着比前一种情况少50000次迭代。完整的代码是文件temporal_differencing_control_sarsa.py中的一部分，您可以在主循环中注释相应行启用或禁用的ε-greedy选项。如何选择ε的值？大多数情况下，0.1的值是一个不错的选择。选择一个太高的值会导致算法收敛太慢，因为要进行太多的探索；相反，太小的值并不能保证访问到所有状态-动作对从而导致趋向次优策略，这个问题被称为探索-利用困境(exploration-exploitation dilemma)，是困扰强化学习的问题之一。现在是引入Q-learning的时候了，是另一种用于TD控制估计的算法。

Q-learning：off-policy控制

Watkins在博士论文中介绍了Q-learning，被认为是强化学习中最重要的算法之一，但大多数没有详细解释。为了了解它的工作原理，在这里我将剖析算法，重点介绍其深层含义。在继续之前，您应该清楚地了解以下概念：

·        广义策略迭代（GPI）（第二篇文章）

·        TD学习中的Target术语（第一节）

·        SARSA的更新规则（前一节）

现在我们继续。在控制场景下，我们总是使用策略π来进行学习，这意味着我们从π采样中获得的经验来更新了π，这种方法被称为on-policy学习。然而，还有另一种学习π的方式被称为off-policy学习。在off-policy学习中，我们不需要策略来更新我们的Q函数。当然，我们仍然可以基于从Q函数获得最大效用的动作生成策略π，但Q函数本身得到改进是基于对第二个不被更新的策略μ的观察。例如考虑应用于4x3网格世界的off-policy算法的前四次迭代，我们可以看到在随机初始化π后状态逐步更新，而策略μ根本不会改变。

哪些是off-policy学习的优势？首先使用off-policy，能够遵循探索性策略学得最优策略，off-policy意味着通过观察来学习。例如，我们可以找到一个最优策略，寻找一个遵循次优策略的机器人。在遵循一个策略时（例如多机器人场景），也可以了解多个策略。此外，在深度强化学习中，我们将看到off-policy如何允许重新使用旧策略产生的旧经验来改进当前的策略（经验重播）。最著名的off-policy TD控制算法被称为Q-Learning。要了解Q-learning的工作原理，让我们看一下它的更新规则：

比较SARSA和Q-learning，你会注意到仅仅只有一个区别：Target。下面说明它们的简单比较：

SARSA 使用GPI来改进策略π，Target是通过基于从策略π采样的动作at+1的Q(st+1,at+1)来估计的，在SARSA中改善π意味着改进由Q(st+1,at+1)返回的估计。在Q学习中，我们有两个策略π和μ，用于估计Q(st,a)的动作值a是直接从Q函数中使用max 操作获取的。Q-learning根据后继状态st+1的贪婪Q值进行更新，而SARSA使用的动作at+1的Q值实际上是从学习的策略中选择的。这使得SARSA成为一种on-policy的算法，因此它的收敛条件在很大程度上取决于学习策略。Q-learning不依赖于策略，也可以在完全随机的情况下实现收敛。现在我想详细说明Target是如何建立在Q-learning上的，首先，让我们记住at+1的值不能从策略μ中抽样，因为它在训练期间没有更新并且使用它会破坏GPI规则，但是，使用Q函数我们可以在每个时间步更新策略π 如下：

这时很明显我们实际上不需要使用策略π来选择动作，而是可以简单地使用右侧的公式，并重写Target作为在st + 1时通过贪婪选择获得的Q值折扣：

下面的表达式对应于t+1时的最高Q值，这意味着它可以被简化为：

就是这样，在实际更新规则中我们使用Target，并且此值遵循GPI规则。现在让我们看看Q-learning中涉及的所有步骤：

1. 移动一步并从μ(st)中选择at

2. 观察：rt+1、st+1

3. 更新状态-动作函数Q(st,at)

4. （可选）更新策略：

SARSA和Q-learning之后的步骤有所不同，不像在SARSA，Q-learning在步骤2不考虑下一步的动作at+1。实际中Q-learning使用State-Action-Reward-State元组来更新状态-动作函数。比较步骤1和步骤4，您可以看到在SARSA的步骤1中，动作是从π采样的然后在步骤4更新相同的策略；在Q-learning的步骤1和步骤4中，动作是从探索性策略μ中采样，并在步骤4（可选）更新的策略π。步骤4是可选的，因为动作值可以直接从Q函数中获得，计算并存储π 是浪费资源。

对于Q-learning，还有一个基于资格痕迹的版本。实际上有两个版本：Watkins的Q(λ)和Peng的Q(λ)。在这里我将关注Watkins的Q(λ)。Watkins在其博士论文中介绍了Q(λ)算法，算法背后的想法与TD（λ）和SARSA(λ)相似。像SARSA(λ)一样，我们更新状态-动作对，但是有一个重要的区别。在Q-learning中有两个策略，一个是用于采样动作的探索性策略μ，另一个是每次迭代更新的目标策略π，因此在动作a以ε-greedy方式被选择时，可以有机会选择探索性动作而不是贪婪性动作。在这种情况下，所有状态-动作对的资格痕迹都会设置为零。

 Isst是一个指示符，当s=st时等于1，Iaat和它相似。估计误差δ被定义为：

我们使用以下更新规则更新Q函数：

不幸的是，在选择探索性的非贪婪动作时切断痕迹失去了使用资格痕迹的许多优点。像SARSA（λ）一样，我不会在下一节中实现Q（λ）算法，然而，Sutton和Barto的书中第7.6章介绍了一个很好的伪代码。

Q-learning:Python实现

该算法的Python实现需要调用一个名为policy_matrix的随机策略和一个名为exploratory_policy_matrix的探索性策略。第一个可以随机初始化，而第二个可以是任何次优策略。每次访问时要执行的动作取自exploratory_policy_matrix，而步骤4的更新规则适用于policy_matrix。该代码与SARSA中使用的代码非常相似，主要区别在于状态操作矩阵的更新规则：

 

def update_state_action(state_action_matrix, observation, new_observation, 
                        action, reward, alpha, gamma):
    '''Return the updated utility matrix

    @param state_action_matrix the matrix before the update
    @param observation the state obsrved at t
    @param new_observation the state observed at t+1
    @param action the action at t
    @param new_action the action at t+1
    @param reward the reward observed after the action
    @param alpha the ste size (learning rate)
    @param gamma the discount factor
    @return the updated state action matrix
    '''
    #Getting the values of Q at t and at t+1
    col = observation[1] + (observation[0]*4)
    q = state_action_matrix[action ,col]
    col_t1 = new_observation[1] + (new_observation[0]*4)
    q_t1 = np.max(state_action_matrix[: ,col_t1])
    #Applying the update rule
    state_action_matrix[action ,col] += alpha * (reward + gamma * q_t1 - q)
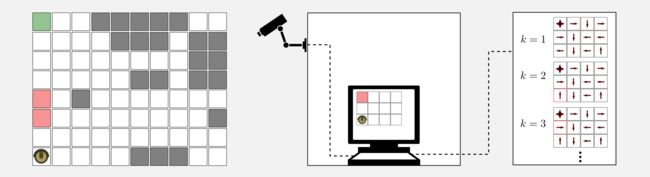
    return state_action_matrix

下面例子将阐明到目前为止所表达的内容。假设您注意到上周购买的清洁机器人在返回充电站时并未遵循最佳策略，而是正在遵循不安全的次优路径。你想找到一个最佳的策略，并向制造商提出升级的建议（并获得采纳！）。但存在一个问题，您无权访问机器人的固件，机器人遵循其内部策略 μ而这个策略是无法访问的。该怎么办？

你可以做的是使用像Q-learning这样的off-policy算法来估计最优策略。首先你使用这个GridWorld类创建一个离散状态版本的房间，其次，你会得到一台相机，并借助一些标记来评估机器人在真实世界中的位置并将其重新定位到网格世界。在每个时间步，你都有机器人的位置和奖励，相机连接到您的工作站，并在工作站上运行Q-learningPython脚本。幸运的是，您不必从头开始编写代码，在GitHub上的dissecting-reinforcement-learning官方存储库中提供了一个很好的启动脚本，名为temporal_differencing_control_qlearning.py。该脚本基于通常的4x3网格世界，但可以轻松扩展到更复杂的场景。

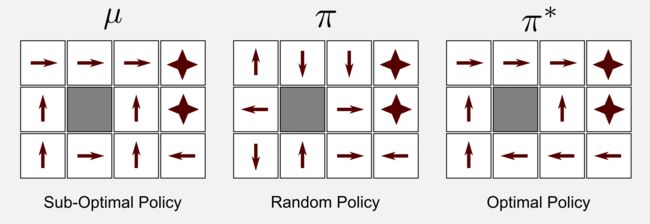
使用alpha=0.001、gamma=0.999和epsilon=0.1运行脚本300000次迭代收敛到最优策略的算法。很好！你有了最佳的策略，但是有两个重要的限制。首先，算法在300000次迭代后收敛，这意味着你需要300000个episode。可能你必须监视机器人几个月才能获得所有这些episode。在确定性环境中，您可以通过观察估计策略μ，然后在模拟环境中运行30万episode。然而，在非确定性的环境中，为了找到运动模型，您需要花费更多的精力，而且这通常非常耗时。第二个限制是最佳策略仅对特定空间设置有效，改变充电站的位置或障碍物的位置策略必须重新学习。我们将在未来的文章中看到如何使用监督学习和神经网络推广到更大的状态空间。现在让我们关注所取得的成果。Q-learning从一个随机策略π开始遵循次优策略μ并且估计最优策略π *。

关于Q-learning的有趣之处在于，当它收敛时策略μ也会是一种对抗策略。我们假设μ尽可能将机器人远离充电站及尽可能靠近楼梯，在这种极端条件下，我们可以预期该算法根本不会收敛。使用与之前相同的参数运行脚本并采用对抗策略，算法在583001次迭代中收敛到最优策略。我们凭经验论证，从一个合适的策略开始可以加速收敛。

结论

这篇文章总结了强化学习中的许多重要概念。TD方法由于其简单性和多功能性而被广泛使用。正如在第二篇文章中，我们将TD方法分为两类：预测和控制。预测TD算法被称为TD(0)，我展示了如何使用资格痕迹，可以延伸到之前的状态，TD(0)与资格痕迹的延伸称为TD(λ)。控制TD中的算法被称为SARSA和Q-learning。前者是一种on-policy算法，在环境中移动时更新策略；后者是一种off-policy算法，它使用两个单独的策略，一个用于更新，另一个用于在世界中移动。TD方法的收敛速度是否比MC方法快？没有数学上的证明，但经验上TD方法收敛速度更快。

 

索引

1. [第一篇]马尔科夫决策过程，贝尔曼方程，值迭代和策略迭代算法。

2.  [第二篇]蒙特卡罗概念，蒙特卡洛方法，预测与控制，广义策略迭代，Q函数。

3.  [第三篇]时间差分概念，动物学习，TD(0), TD(λ)和资格痕迹，SARSA，Q-learning。

4.  [第四篇]Actor-Critic方法背后的神经生物学，计算Actor-Critic方法，Actor-only和Critic-only方法。

5.  [第五篇]进化算法介绍，强化学习中的遗传算法，遗传算法的策略选择。

6.  [第六篇]强化学习应用，多臂老虎机，山地车，倒立摆，无人机着陆，难题。

7.  [第七篇]函数逼近概念，线性逼近器，应用，高阶逼近器。

8. [第八篇] 非线性函数逼近，感知器，多层感知器，应用，政策梯度。

资源

·   The complete code for TD predictionand TD control is available on the dissecting-reinforcement-learning officialrepository on GitHub.

·        Dadid Silver’s course (DeepMind) in particular lesson 4 [pdf][video]and lesson 5 [pdf][video]

·        Christopher Watkins doctoraldissertation, which introduced the Q-learning for the firsttime [pdf]

·        Machine Learning Mitchell T.(1997) [web]

·        Artificialintelligence: a modern approach. (chapters 17 and 21)Russell, S. J.,Norvig, P., Canny, J. F., Malik, J. M., & Edwards, D. D. (2003). UpperSaddle River: Prentice hall. [web] [github]

·        Reinforcement learning:An introduction. Sutton, R. S., & Barto, A. G. (1998). Cambridge: MITpress. [html]

·        Reinforcement learning:An introduction (second edition). Sutton, R. S., &Barto, A. G. (in progress). [pdf]

参考

Bellman,R. (1957). A Markovian decision process (No. P-1066). RAND CORP SANTA MONICACA.

Rescorla,R. A., & Wagner, A. R. (1972). A theory of Pavlovian conditioning:Variations in the effectiveness of reinforcement and nonreinforcement.Classical conditioning II: Current research and theory, 2, 64-99.

Rummery,G. A., & Niranjan, M. (1994). On-line Q-learning using connectionistsystems. University of Cambridge, Department of Engineering.

Russell,S. J., Norvig, P., Canny, J. F., Malik, J. M., & Edwards, D. D. (2003).Artificial intelligence: a modern approach (Vol. 2). Upper Saddle River:Prentice hall.

Sutton,R. S. (1988). Learning to predict by the methods of temporal differences.Machine learning, 3(1), 9-44.

Sutton,R. S., & Barto, A. G. (1990). Time-derivative models of pavlovianreinforcement.

Watkins,C. J. C. H. (1989). Learning from delayed rewards (Doctoral dissertation,University of Cambridge).